
 函數解析式的求解;
函數解析式的求解; 函數定義域的求解.
函數定義域的求解.
 (
( 全國Ⅰ)設
全國Ⅰ)設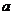 是實數,且
是實數,且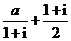 是實數,則
是實數,則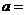

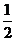

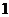

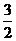

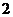
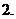 (
( 全國Ⅱ)設復數
全國Ⅱ)設復數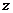 滿足
滿足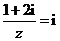 ,則
,則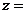

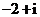



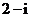

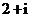
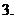 (
( 北京)
北京)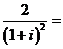
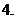 (
( 福建)復數
福建)復數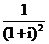 等于
等于

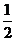

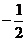

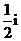

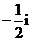
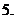 (
( 安徽)若
安徽)若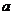 為實數,
為實數,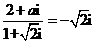 ,則
,則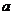 等于
等于

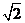

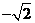

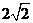

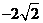
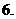 (
( 天津)是虛數單位,
天津)是虛數單位,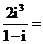

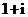

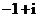

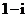

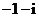
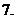 (
( 四川)復數
四川)復數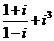 的值是
的值是

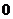

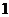

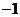

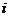
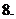 (
( 江西)化簡
江西)化簡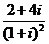 的結果是
的結果是

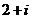

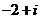

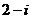

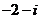
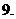 (
( 湖南)復數
湖南)復數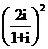 等于
等于

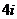

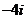

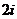

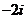
 (
( 湖北)復數
湖北)復數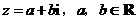 ,且
,且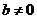 ,若
,若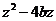 是實數,則有序實數對
是實數,則有序實數對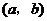 可以是
(寫出一個有序實數對即可)
可以是
(寫出一個有序實數對即可)
 (
( 上海,
上海,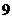 )對于非零實數
)對于非零實數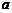 、
、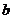 ,以下四個命題都成立:
,以下四個命題都成立:
① 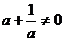 ;
②
;
② 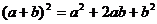 ;
;
③ 若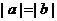 ,則
,則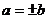 ; ④ 若
; ④ 若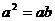 ,則
,則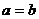 .
.
那么,對于非零復數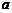 、
、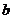 ,仍然成立的命題的所有序號是
,仍然成立的命題的所有序號是
 (
( 重慶)復數
重慶)復數 的虛部為
的虛部為
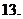 (
( 浙江)已知復數
浙江)已知復數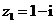 ,
,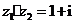 ,則復數
,則復數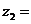
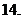 (
( 上海)若復數
上海)若復數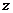 同時滿足
同時滿足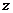 -
-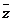 =
=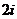 ,
,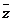 =
=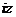 (
(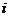 為虛數單位),則
為虛數單位),則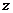 =
=
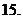 (
( 浙江)已知
浙江)已知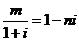 ,其中
,其中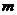 、
、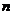 是實數,
是實數,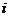 是虛數單位,則
是虛數單位,則

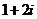

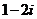

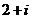

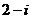
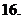 (
(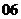 湖北)設
湖北)設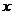 、
、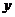 為實數,且
為實數,且 ,則
,則
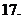 (
(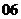 福建)設
福建)設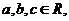 則復數
則復數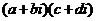 為實數的充要條件是( )
為實數的充要條件是( )

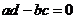

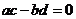

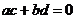

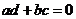
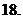 (
( 江西)已知復數
江西)已知復數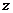 滿足
滿足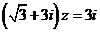 ,則
,則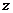 =
=

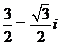

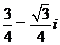

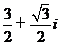

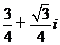
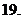 (
( 全國Ⅰ)如果復數
全國Ⅰ)如果復數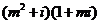 是實數,則實數
是實數,則實數

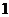

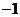

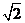

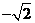
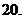 (
(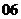 四川)復數
四川)復數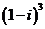 的虛部為
的虛部為

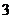

 .
. 
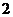

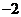
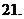 (
( 重慶)復數
重慶)復數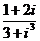 的值是
的值是
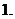 虛數單位
虛數單位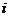 :
:
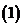 它的平方等于
它的平方等于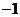 ,即
,即 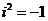 ;
;
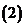 實數可以與它進行四則運算,進行四則運算時,原有加、乘運算律仍然成立.
實數可以與它進行四則運算,進行四則運算時,原有加、乘運算律仍然成立.
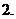
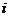 與-1的關系:
與-1的關系: 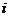 就是
就是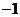 的一個平方根,即方程
的一個平方根,即方程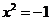 的一個根,方程
的一個根,方程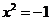 的另一個根是
的另一個根是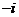 .
.
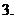
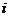 的周期性:
的周期性: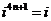 ,
, 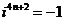 ,
,  ,
,  .
.
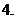 復數的定義:形如
復數的定義:形如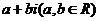 的數叫復數,
的數叫復數,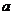 叫復數的實部,
叫復數的實部,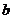 叫復數的虛部.全體復數所成的集合叫做復數集,用字母
叫復數的虛部.全體復數所成的集合叫做復數集,用字母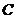 表示
表示
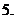 復數的代數形式: 復數通常用字母
復數的代數形式: 復數通常用字母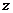 表示,即
表示,即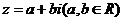 ,把復數表示成
,把復數表示成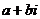 的形式,叫做復數的代數形式.
的形式,叫做復數的代數形式.
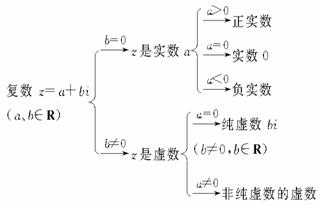
 復數與實數、虛數、純虛數及
復數與實數、虛數、純虛數及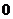 的關系:對于復數
的關系:對于復數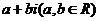 ,當且僅當
,當且僅當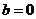 時,復數
時,復數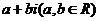 是實數
是實數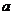 ;當
;當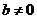 時,復數
時,復數 叫做虛數;當
叫做虛數;當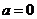 且
且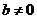 時,
時,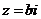 叫做純虛數;當且僅當
叫做純虛數;當且僅當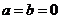 時,
時,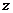 就是實數
就是實數
 復數集與其它數集之間的關系:
復數集與其它數集之間的關系: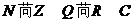
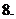 兩個復數相等的定義:如果兩個復數的實部和虛部分別相等,那么我們就說這兩個復數相等.這就是說,如果
兩個復數相等的定義:如果兩個復數的實部和虛部分別相等,那么我們就說這兩個復數相等.這就是說,如果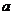 ,
,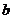 ,
,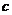 ,
,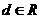 ,那么
,那么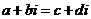
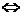
 ,
,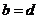
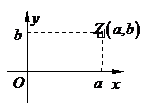
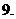 復平面、實軸、虛軸:復數
復平面、實軸、虛軸:復數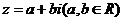 與有序實數
與有序實數
對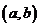 是一一對應關系.建立一一對應的關系.點
是一一對應關系.建立一一對應的關系.點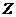 的橫坐標是
的橫坐標是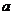 ,
,
縱坐標是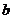 ,復數
,復數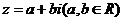 可用點
可用點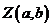 表示,這個
表示,這個
建立了直角坐標系來表示復數的平面叫做復平面,也叫高斯平面,
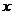 軸叫做實軸,
軸叫做實軸,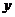 軸叫做虛軸.實軸上的點都表示實數.
軸叫做虛軸.實軸上的點都表示實數.
對于虛軸上的點要除原點外,因為原點對應的有序實數對為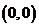 , 它所確定的復數是
, 它所確定的復數是 表示是實數.故除了原點外,虛軸上的點都表示純虛數.
表示是實數.故除了原點外,虛軸上的點都表示純虛數.
復數
 復平面內的點
復平面內的點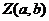
這就是復數的一種幾何意義.也就是復數的另一種表示方法,即幾何表示方法.
 復數
復數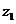 與
與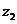 的和的定義:
的和的定義: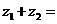
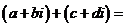
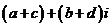
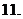 復數
復數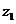 與
與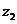 的差的定義:
的差的定義: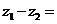
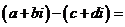
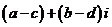
 復數的加法運算滿足交換律:
復數的加法運算滿足交換律: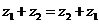
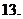 復數的加法運算滿足結合律:
復數的加法運算滿足結合律: 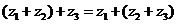
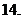 乘法運算規則:
乘法運算規則:
設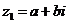 ,
,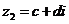 (
(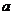 、
、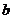 、
、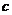 、
、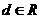 )是任意兩個復數,那么它們的積
)是任意兩個復數,那么它們的積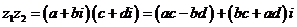
其實就是把兩個復數相乘,類似兩個多項式相乘,在所得的結果中把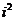 換成
換成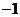 ,并且把實部與虛部分別合并.兩個復數的積仍然是一個復數.
,并且把實部與虛部分別合并.兩個復數的積仍然是一個復數.
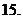 乘法運算律:
乘法運算律:
(1)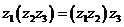
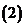
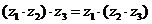
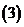
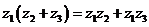
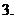 復數除法定義:滿足
復數除法定義:滿足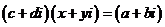 的復數
的復數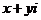 (
(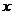 、
、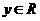 )叫復數
)叫復數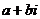 除以復數
除以復數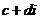 的商,記為:
的商,記為: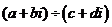 或者
或者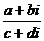
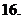 除法運算規則:
除法運算規則:
①設復數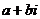 (
(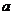 、
、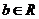 ),除以
),除以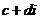 (
(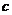 ,
,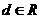 ),其商為
),其商為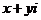 (
(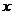 、
、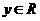 ),
),
即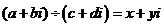 ∵
∵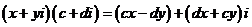
∴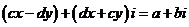
由復數相等定義可知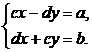 解這個方程組,得
解這個方程組,得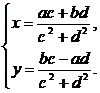
于是有: 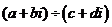
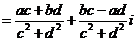
②利用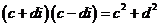 于是將
于是將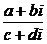 的分母有理化得:
的分母有理化得:
原式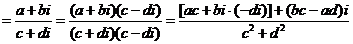
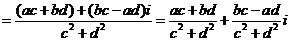 .
.
∴(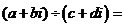
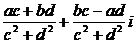
點評:①是常規方法,②是利用初中我們學習的化簡無理分式時,都是采用的分母有理化思想方法,而復數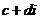 與復數
與復數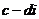 ,相當于我們初中學習的
,相當于我們初中學習的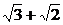 的對偶式
的對偶式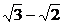 ,它們之積為
,它們之積為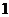 是有理數,而
是有理數,而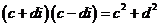 是正實數.所以可以分母實數化. 把這種方法叫做分母實數化法.
是正實數.所以可以分母實數化. 把這種方法叫做分母實數化法.
 共軛復數:當兩個復數的實部相等,虛部互為相反數時,這兩個復數叫做互為共軛復數。虛部不等于
共軛復數:當兩個復數的實部相等,虛部互為相反數時,這兩個復數叫做互為共軛復數。虛部不等于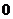 的兩個共軛復數也叫做共軛虛數.
的兩個共軛復數也叫做共軛虛數.
 (
( 陜西)
陜西) 是定義在
是定義在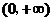 上的非負可導函數,且滿足
上的非負可導函數,且滿足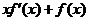 ≤
≤ .
.
對任意正數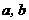 ,若
,若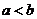 ,則必有
,則必有

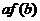 ≤
≤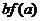

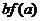 ≤
≤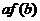

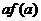 ≤
≤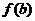

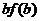 ≤
≤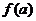
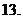 (
(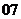 江蘇)已知二次函數
江蘇)已知二次函數 的導數為
的導數為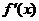 ,
, ,對于任意實數
,對于任意實數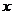 ,有
,有 ≥
≥ ,則
,則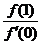 的最小值為
的最小值為 
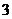

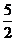

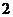

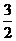
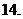 (
( 全國)函數
全國)函數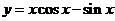 在下面哪個區間內是增函數
在下面哪個區間內是增函數

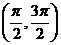

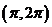

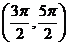

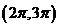
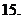 (
( 重慶)曲線
重慶)曲線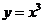 在點
在點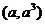
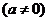 處的切線與
處的切線與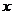 軸、直線
軸、直線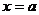 所圍成的三角形的面積為
所圍成的三角形的面積為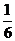 ,則
,則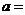
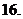 (
(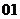 全國)已知
全國)已知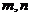 是正整數且
是正整數且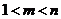 ,求證:
,求證: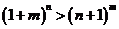
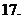 (
( 重慶)已知函數
重慶)已知函數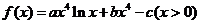 在
在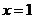 處取得極值
處取得極值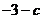 ,其中
,其中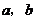 為常數.(Ⅰ)試確定
為常數.(Ⅰ)試確定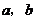 的值;(Ⅱ)討論函數
的值;(Ⅱ)討論函數 的單調區間;
的單調區間;
(Ⅲ)若對任意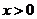 ,不等式
,不等式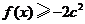 恒成立,求
恒成立,求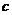 的取值范圍.
的取值范圍.
 (
( 海南)設函數
海南)設函數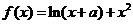
(Ⅰ)若當 時,
時, 取得極值,求
取得極值,求 的值,并討論
的值,并討論 的單調性;
的單調性;
(Ⅱ)若 存在極值,求
存在極值,求 的取值范圍,并證明所有極值之和大于
的取值范圍,并證明所有極值之和大于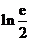 .
.
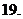 (
( 全國Ⅰ)設函數
全國Ⅰ)設函數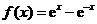 .
.
(Ⅰ)證明: 的導數
的導數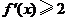 ;
;
(Ⅱ)若對所有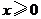 都有
都有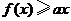 ,求
,求 的取值范圍.
的取值范圍.
 (
( 全國Ⅱ文)若函數
全國Ⅱ文)若函數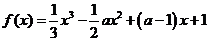 在區間
在區間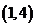 內為減函數,在區間
內為減函數,在區間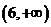 內為增函數,試求實數
內為增函數,試求實數 的取值范圍.
的取值范圍.
 已知函數
已知函數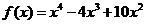 ,則方程
,則方程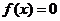 在區間
在區間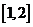 上的根有
上的根有

 個
個

 個
個

 個
個 
 個
個
 (
(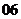 鄭州一中等四校聯考)若函數
鄭州一中等四校聯考)若函數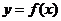 在
在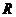 上可導且滿足不等式
上可導且滿足不等式
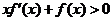 恒成立,且常數
恒成立,且常數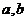 滿足
滿足 ,則下列不等式一定成立的是
,則下列不等式一定成立的是

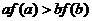

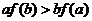

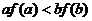

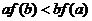
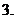 求滿足條件的
求滿足條件的 的范圍:
的范圍:
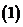 使
使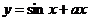 為
為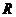 上增函數,則
上增函數,則 的范圍是
的范圍是
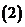 使
使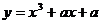 為
為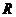 上增函數,則
上增函數,則 的范圍是
的范圍是
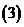 使
使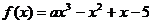 為
為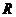 上增函數,則
上增函數,則 的范圍是
的范圍是
 證明方程
證明方程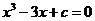 在
在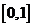 上至多有一實根.
上至多有一實根.
 (
( 屆高三陜師大附中八模)如果
屆高三陜師大附中八模)如果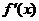 是二次函數, 且
是二次函數, 且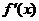 的圖象開口向上,
的圖象開口向上,
頂點坐標為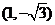 , 那么曲線
, 那么曲線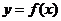 上任一點的切線的傾斜角
上任一點的切線的傾斜角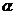 的取值范圍是
的取值范圍是

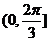



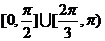

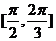
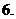 (
( 屆廈門雙十中學高三月考)如圖,是函數
屆廈門雙十中學高三月考)如圖,是函數
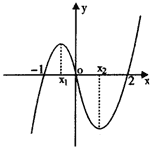
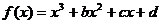 的大致圖像,
的大致圖像,
|
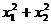 等于
等于

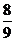

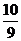

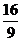


 (
(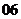 天津)函數
天津)函數 的定義域是開區間
的定義域是開區間 ,
,
導函數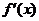 在
在 內的圖象如圖所示,則函數
內的圖象如圖所示,則函數
 在開區間內有極小值點
在開區間內有極小值點
 個
個 
 個
個 
 個
個 
 個
個
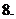 (
( 屆高三哈爾濱第三中學第一次月考)
屆高三哈爾濱第三中學第一次月考)
函數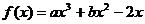 的圖象如圖所示,
的圖象如圖所示,
且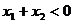 ,則有
,則有

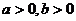

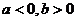

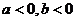

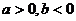
 已知:
已知: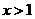 ,證明不等式:
,證明不等式: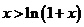
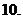 設
設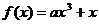 恰有三個單調區間,試確定
恰有三個單調區間,試確定 的取值范圍,并求出這三個單調區間
的取值范圍,并求出這三個單調區間
 (
( 屆高三福建質檢)已知函數
屆高三福建質檢)已知函數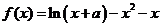 在
在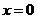 處取得極值.
處取得極值. 求實數
求實數 的值;
的值;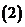 若關于
若關于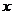 的方程
的方程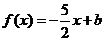 在區間
在區間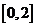 上恰有兩個不同的實數根,求實數
上恰有兩個不同的實數根,求實數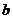 的取值范圍;
的取值范圍;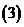 證明:對任意的正整數
證明:對任意的正整數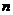 ,不等式
,不等式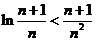 都成立.
都成立.
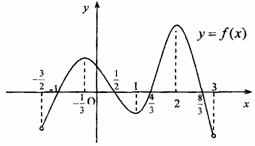
問題1. (
( 屆云南平遠一中五模)函數
屆云南平遠一中五模)函數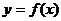 在定義域
在定義域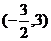 內可導,其圖象如圖所示,記
內可導,其圖象如圖所示,記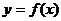 的導函數為
的導函數為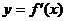 ,則不等式
,則不等式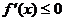 的解集為
的解集為





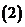 已知
已知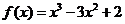 ,
,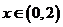 的反函數為
的反函數為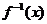 ,則
,則

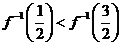

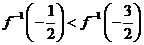

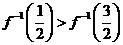


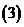 (
( 大連一模)設
大連一模)設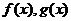 均是定義在
均是定義在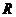 上的奇函數,當
上的奇函數,當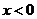 時,
時,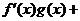
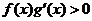 ,且
,且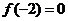 ,則不等式
,則不等式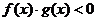 的解集是
的解集是

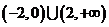

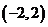

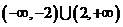

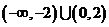
問題2.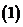 如果函數
如果函數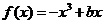 在區間
在區間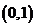 上單調遞增,并且方程
上單調遞增,并且方程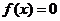 的根都在區間
的根都在區間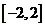 內,則
內,則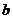 的取值范圍為
的取值范圍為
 (
( 屆高三浙江上虞市調研)已知
屆高三浙江上虞市調研)已知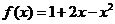 ,那么
,那么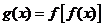
 在區間
在區間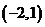 上單調遞增
上單調遞增  在
在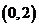 上單調遞增
上單調遞增
 在
在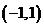 上單調遞增
上單調遞增
 在
在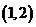 上單調遞增
上單調遞增
 函數
函數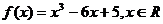 ,
,
(Ⅰ)求 的單調區間和極值;
的單調區間和極值;
(Ⅱ)若關于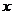 的方程
的方程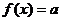 有
有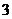 個不同實根,求實數
個不同實根,求實數 的取值范圍.
的取值范圍.
(Ⅲ)已知當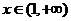 時,
時, ≥
≥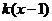 恒成立,求實數
恒成立,求實數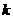 的取值范圍.
的取值范圍.
問題3.(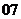 天津)已知函數
天津)已知函數
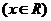 ,其中
,其中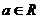 .
.
(Ⅰ)當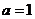 時,求曲線
時,求曲線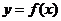 在點
在點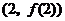 處的切線方程;
處的切線方程;
(Ⅱ)當 時,求函數
時,求函數 的單調區間與極值.
的單調區間與極值.
問題4.(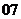 湖北)已知定義在正實數集上的函數
湖北)已知定義在正實數集上的函數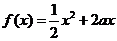 ,
, ,其中
,其中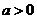 .設兩曲線
.設兩曲線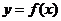 ,
,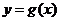 有公共點,且在該點處的切線相同.(Ⅰ)用
有公共點,且在該點處的切線相同.(Ⅰ)用 表示
表示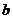 ,并求
,并求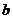 的最大值;(Ⅱ)求證:
的最大值;(Ⅱ)求證: ≥
≥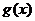 (
(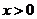 ).
).
問題5.利用導數求和:
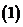
 (
(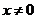 ,
, 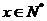 ).
).
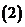
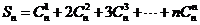 (
(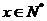 ).
).
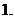 利用導數研究多項式函數單調性的一般步驟:
利用導數研究多項式函數單調性的一般步驟:
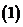 求
求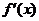 ;
;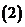 確定
確定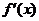 在
在 內符號;
內符號;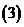 若
若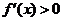 在
在 上恒成立,則
上恒成立,則 在
在 上是增函數;若
上是增函數;若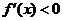 在
在 上恒成立,則
上恒成立,則 在
在 上是減函數
上是減函數
①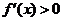
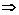
 為增函數(
為增函數(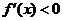
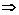
 為減函數).
為減函數).
② 在區間
在區間 上是增函數
上是增函數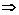
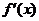 ≥
≥ 在
在 上恒成立;
上恒成立;
 在區間
在區間 上為減函數
上為減函數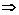
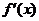 ≤
≤ 在
在 上恒成立.
上恒成立.
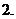 極大值: 一般地,設函數
極大值: 一般地,設函數 在點
在點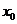 附近有定義,如果對
附近有定義,如果對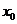 附近的所有的點,都有
附近的所有的點,都有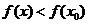 ,就說
,就說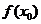 是函數
是函數 的一個極大值,記作
的一個極大值,記作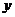 極大值
極大值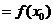 ,
,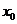 是極大值點.
是極大值點.
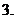 極小值:一般地,設函數
極小值:一般地,設函數 在
在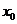 附近有定義,如果對
附近有定義,如果對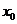 附近的所有的點,都有
附近的所有的點,都有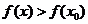 就說
就說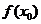 是函數
是函數 的一個極小值,記作
的一個極小值,記作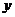 極小值
極小值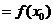 ,
,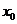 是極小值點.
是極小值點.
 極大值與極小值統稱為極值
極大值與極小值統稱為極值
在定義中,取得極值的點稱為極值點,極值點是自變量的值,極值指的是函數值 請注意以下幾點:
請注意以下幾點:
(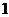 )極值是一個局部概念
)極值是一個局部概念 由定義,極值只是某個點的函數值與它附近點的函數值比較是最大或最小.并不意味著它在函數的整個的定義域內最大或最小.
由定義,極值只是某個點的函數值與它附近點的函數值比較是最大或最小.并不意味著它在函數的整個的定義域內最大或最小.
(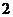 )函數的極值不是唯一的
)函數的極值不是唯一的 即一個函數在某區間上或定義域內極xs大值或極小值可以不止一個.
即一個函數在某區間上或定義域內極xs大值或極小值可以不止一個.
(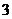 )極大值與極小值之間無確定的大小關系
)極大值與極小值之間無確定的大小關系 即一個函數的極大值未必大于極小值,如下圖所示,
即一個函數的極大值未必大于極小值,如下圖所示,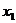 是極大值點,
是極大值點,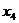 是極小值點,而
是極小值點,而 >
>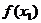 .
.
( )函數的極值點一定出現在區間的內部,區間的端點不能成為極值點
)函數的極值點一定出現在區間的內部,區間的端點不能成為極值點 而使函數取得最大值、最小值的點可能在區間的內部,也可能在區間的端點.
而使函數取得最大值、最小值的點可能在區間的內部,也可能在區間的端點.
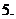 當
當 在點
在點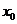 連續時,判別
連續時,判別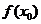 是極大、極小值的方法:
是極大、極小值的方法:
若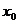 滿足
滿足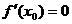 ,且在
,且在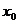 的兩側
的兩側 的導數異號,則
的導數異號,則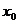 是
是 的極值點,
的極值點,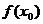 是極值,并且如果
是極值,并且如果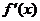 在
在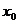 兩側滿足“左正右負”,則
兩側滿足“左正右負”,則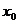 是
是 的極大值點,
的極大值點,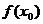 是極大值;如果
是極大值;如果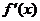 在
在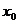 兩側滿足“左負右正”,則
兩側滿足“左負右正”,則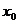 是
是 的極小值點,
的極小值點,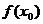 是極小值.
是極小值.
 求可導函數
求可導函數 的極值的步驟:
的極值的步驟:
 確定函數的定義區間,求導數
確定函數的定義區間,求導數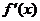
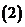 求方程
求方程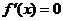 的根
的根
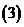 用函數的導數為
用函數的導數為 的點,順次將函數的定義區間分成若干小開區間,并列成表格.檢查
的點,順次將函數的定義區間分成若干小開區間,并列成表格.檢查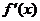 在方程根左右的值的符號,如果左正右負,那么
在方程根左右的值的符號,如果左正右負,那么 在這個根處取得極大值;如果左負右正,那么
在這個根處取得極大值;如果左負右正,那么 在這個根處取得極小值;如果左右不改變符號,那么
在這個根處取得極小值;如果左右不改變符號,那么 在這個根處無極值.如果函數在某些點處連續但不可導,也需要考慮這些點是否是極值點 .
在這個根處無極值.如果函數在某些點處連續但不可導,也需要考慮這些點是否是極值點 .
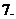 函數的最大值和最小值: 一般地,在閉區間
函數的最大值和最小值: 一般地,在閉區間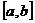 上連續的函數
上連續的函數 在
在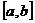 上必有最大值與最小值.
上必有最大值與最小值.
說明: 在開區間
在開區間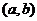 內連續的函數
內連續的函數 不一定有最大值與最小值.如函數
不一定有最大值與最小值.如函數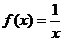 在
在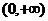 內連續,但沒有最大值與最小值;
內連續,但沒有最大值與最小值;
 函數的最值是比較整個定義域內的函數值得出的;函數的極值是比較極值點附近函數值得出的.
函數的最值是比較整個定義域內的函數值得出的;函數的極值是比較極值點附近函數值得出的.
 函數
函數 在閉區間
在閉區間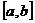 上連續,是
上連續,是 在閉區間
在閉區間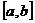 上有最大值與最小值的充分條件而非必要條件.
上有最大值與最小值的充分條件而非必要條件.
 函數在其定義區間上的最大值、最小值最多各有一個,而函數的極值可能不止一個,也可能沒有一個.
函數在其定義區間上的最大值、最小值最多各有一個,而函數的極值可能不止一個,也可能沒有一個.
 利用導數求函數的最值步驟:
利用導數求函數的最值步驟:
由上面函數 的圖象可以看出,只要把連續函數所有的極值與定義區間端點的函數值進行比較,就可以得出函數的最值了.
的圖象可以看出,只要把連續函數所有的極值與定義區間端點的函數值進行比較,就可以得出函數的最值了.
設函數 在
在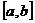 上連續,在
上連續,在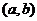 內可導,則求
內可導,則求 在
在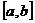 上的最大值與最小值的步驟如下:
上的最大值與最小值的步驟如下: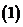 求
求 在
在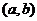 內的極值;
內的極值;
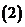 將
將 的各極值與
的各極值與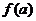 、
、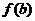 比較得出函數
比較得出函數 在
在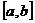 上的最值
上的最值 p
p
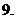 求參數范圍的方法:①分離變量法;②構造(差)函數法.
求參數范圍的方法:①分離變量法;②構造(差)函數法.
 構造函數法是證明不等式的常用方法:構造時要注意四變原則:變具體為抽象,變常量為變量,變主元為輔元,變分式為整式.
構造函數法是證明不等式的常用方法:構造時要注意四變原則:變具體為抽象,變常量為變量,變主元為輔元,變分式為整式.
 通過求導求函數不等式的基本思路是:以導函數和不等式為基礎,單調性為主線,最(極值)為助手,從數形結合、分類討論等多視角進行綜合探索.
通過求導求函數不等式的基本思路是:以導函數和不等式為基礎,單調性為主線,最(極值)為助手,從數形結合、分類討論等多視角進行綜合探索.
 (
( 陜西)為確保信息安全,信息需加密傳輸,發送方由明文→密文(加密),接收方由密文→明文(解密),已知加密規則為:明文
陜西)為確保信息安全,信息需加密傳輸,發送方由明文→密文(加密),接收方由密文→明文(解密),已知加密規則為:明文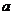 、
、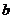 、
、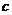 、
、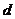 對應密文
對應密文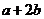 ,
,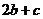 ,
,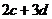 ,
,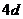 .例如:明文
.例如:明文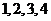 對應密文
對應密文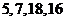 .當接收方收到密文
.當接收方收到密文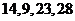 時,則解密得到的明文為
時,則解密得到的明文為



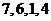




 (
( 浙江)函數
浙江)函數 :
: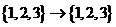 滿足
滿足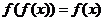 ,則這樣的函數個數
,則這樣的函數個數
共有 
 個
個 
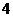 個
個 
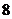 個
個 
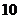 個
個
 (
(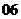 廣東文)對于任意的兩個實數對
廣東文)對于任意的兩個實數對 和
和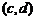 ,規定:
,規定: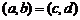 ,
,
當且僅當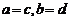 ;運算“
;運算“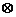 ”為:
”為: ;
;
運算“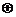 ”為:
”為: ,設
,設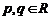 ,若
,若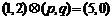 ,
,
則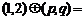



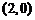

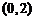

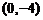
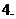 (
(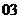 全國)已知
全國)已知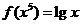 ,則
,則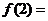 (
)
(
)

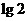

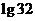

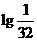

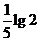
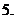 (
(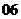 山東文)設
山東文)設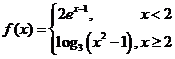 ,則
,則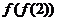 的值為
的值為








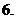 (
( 北京)已知函數
北京)已知函數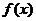 ,
, 分別由下表給出:
分別由下表給出:
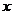







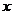



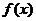



則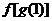 的值為 ;滿足
的值為 ;滿足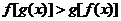 的
的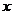 的值是
的值是
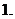
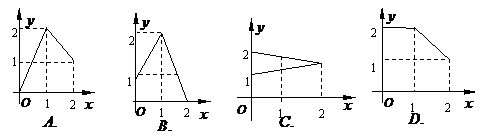 設
設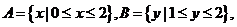 在下圖中,能表示從集合
在下圖中,能表示從集合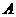 到集合
到集合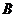 的映射是
的映射是
 已知從集合
已知從集合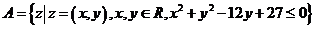 到集合
到集合 的映射
的映射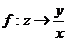 ,則該映射的象集為
,則該映射的象集為



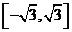

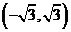
 以上都不對
以上都不對
 (
( 北京東城模擬)設映射
北京東城模擬)設映射 :
: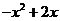 是實數集
是實數集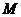 到實數集
到實數集 的映射,若對于實數
的映射,若對于實數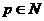 ,在
,在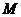 中不存在原象,則
中不存在原象,則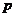 的取值范圍是
的取值范圍是
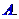
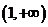

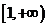

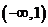

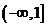
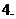 設集合
設集合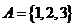 ,
,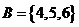 ,定義映射
,定義映射 :
: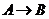 ,使對任意
,使對任意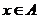 ,都有
,都有 是奇數,則這樣的映射
是奇數,則這樣的映射 的個數為
的個數為




 若
若 ,則
,則 )
)






 已知
已知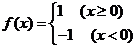 ,則不等式
,則不等式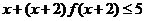 的解集是
的解集是
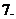 設
設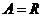 ,
, ,
, :
: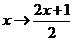 是
是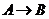 的映射,
的映射,
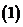 設
設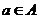 ,則
,則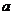 在
在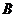 中的象是什么?
中的象是什么?
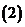 設
設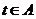 ,那么
,那么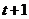 在
在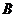 中的象是什么?
中的象是什么?
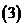 設
設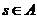 ,若
,若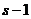 在映射
在映射 下的象為
下的象為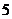 ,則
,則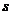 應是多少?
應是多少?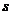 在映射
在映射 的象是什么?
的象是什么?
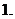
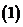
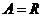 ,
,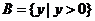 ,
,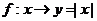 ;
;
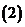
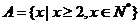 ,
,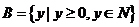 ,
, ;
;
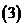
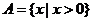 ,
,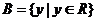 ,
,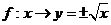 .
.
上述三個對應
是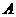 到
到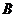 的映射.
的映射.
 給定映射
給定映射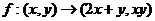 ,點
,點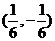 的原象是
的原象是
 下列函數中,與函數
下列函數中,與函數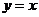 相同的函數是
相同的函數是

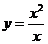

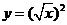

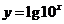

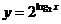
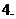 設函數
設函數 ,則
,則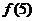 =
=
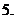 (
( 湖北八校一聯)設
湖北八校一聯)設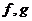 都是由
都是由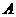 到
到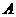 的映射,其對應法則如下表(從上到下):
的映射,其對應法則如下表(從上到下):
表一 映射 的對應法則
表二 映射
的對應法則
表二 映射 的對應法則
的對應法則
|
原象 |
 |
 |
 |
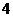 |
|
象 |
 |
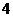 |
 |
 |
|
原象 |
 |
 |
 |
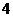 |
|
象 |
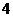 |
 |
 |
 |
則與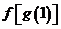 相同的是
相同的是 
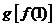

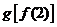

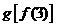

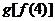
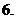 (
( 灌云模擬)設
灌云模擬)設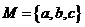 ,從
,從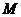 到
到 的映射
的映射 滿足
滿足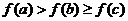 ,
,
試確定這樣的映射 的個數為
的個數為 






湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com