
22. (1)∵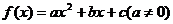 ,
,
∴ 由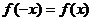 有
有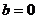 ,得
,得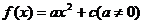 . ……………………2分
. ……………………2分
又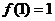 ,
,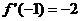 ,
,
∴ 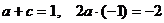 ,
,
解得 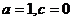 ,因此
,因此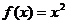 . ……………………5分
. ……………………5分
(2)∵ 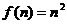
∴ 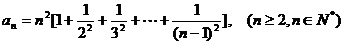 ,
,
于是 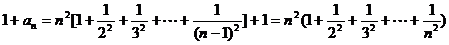 ,
,
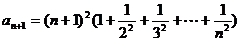 ,
,
因此 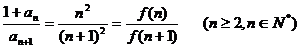 . ……………………9分
. ……………………9分
(3) 由題意可得 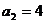 ;當
;當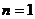 時,有
時,有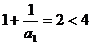 . ……………10分
. ……………10分
當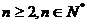 時,
時,
不等式左邊=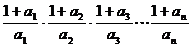
=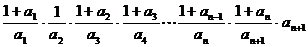 =
=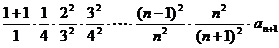 =
=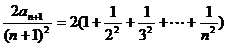 ……………………12分
……………………12分
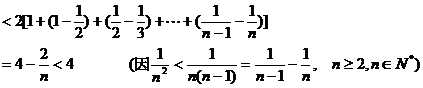
所以,對任意 有
有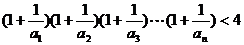 ……………………14分
……………………14分
21. (1)因為原點為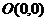 ,所以動點
,所以動點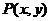 到原點的距離為
到原點的距離為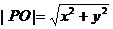 ,
,
∴ 動點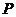 的坐標滿足
的坐標滿足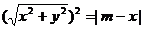 ,
,
∴ 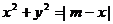 ,此即為動點
,此即為動點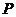 的軌跡方程. ……………………4分
的軌跡方程. ……………………4分
(2) 由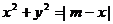 ,兩邊平方,移項因式分解,
,兩邊平方,移項因式分解,
得 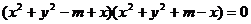 ,
,
∴ 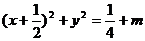 或
或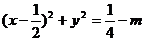 . ……………………6分
. ……………………6分

① 當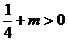 且
且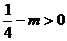 ,即
,即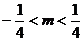 時,點
時,點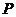 的軌跡是兩個圓.一個圓的圓心是
的軌跡是兩個圓.一個圓的圓心是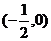 ,半徑為
,半徑為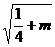 ;一個圓的圓心是
;一個圓的圓心是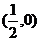 ,半徑為
,半徑為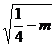 .……………………8分
.……………………8分
② 當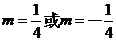 時,點
時,點 的軌跡是一個圓和一個點. ……………………10分
的軌跡是一個圓和一個點. ……………………10分
③ 當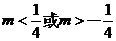 時,點
時,點 的軌跡是一個圓. ……………………12分
的軌跡是一個圓. ……………………12分
20. (1)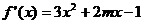 . ………………………………2分
. ………………………………2分
由題意 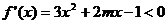 的解集是
的解集是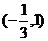 ,
,
即 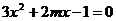 的兩根分別是
的兩根分別是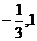 . ………………………………4分
. ………………………………4分
將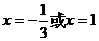 代入方程
代入方程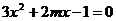 得
得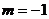 .
.
∴ 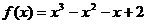 . ………………………………6分
. ………………………………6分
(2) 由題意知 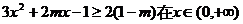 時恒成立,
時恒成立,
即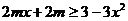 ,所以
,所以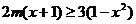 .
.
由于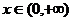 ,于是
,于是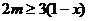 ,得
,得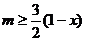 ……………9分
……………9分
而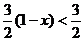 ,所以
,所以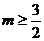 為所求. ………………………………12分
為所求. ………………………………12分
19. (1)張寧以2:1獲勝即前兩局戰成1:1,第三局張寧勝.
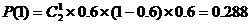 . ………………………………6分
. ………………………………6分
(2) 張寧失利包括0:2和1:2兩種情況:
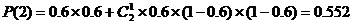 …………12分
…………12分
18. (1)∵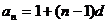 ,
,
∴ 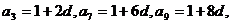 ………………………………3分
………………………………3分
于是 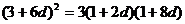 ,
,
注意到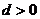 ,得
,得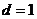 ,所以
,所以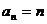 . ………………………………6分
. ………………………………6分
(2) 因為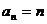 ,所以
,所以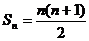 ,于是
,于是
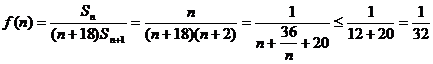
當且僅當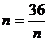 ,即
,即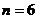 時,
時,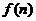 的最大值為
的最大值為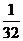 . ………………12分
. ………………12分
17. (1)由已知,可得 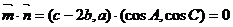 ,
,
即 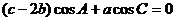 . ………………………………2分
. ………………………………2分
由正弦定理,得 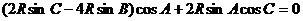 ,
,
∴ 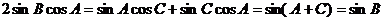 ,
,
由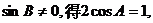 ∴
∴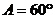 . ………………………………6分
. ………………………………6分
法二 由余弦定理,得 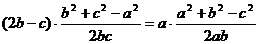 ,
,
∴ 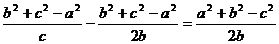 ,
,
∴ 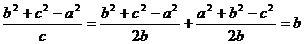 ,
,
∴ 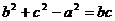 .于是由
.于是由 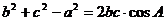 ,
,
得 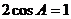 ,∴
,∴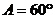 .
.
(2)由已知,得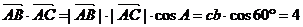 ,
,
∴ 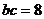 ………………………………9分
………………………………9分
∴ 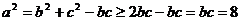 ,即
,即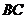 的最小值為
的最小值為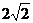 .
.
………………………………12分
DCBA ADBA CDCB
22.(本小題滿分12分)已知二次函數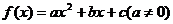 的導函數為
的導函數為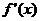 ,且
,且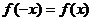 ,
,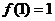 ,
,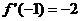 .數列
.數列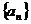 滿足
滿足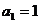 ,且當
,且當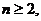
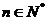 時,
時,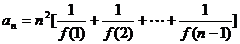 .
.
(1)求函數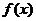 的解析式;
的解析式;
(2) 求證: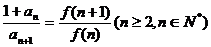 ;
(3)求證:
;
(3)求證: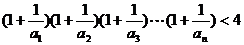 .
.
綿陽市高中2009級第二次診斷性考試
數學(文科)參考解答及評分標準
21. (本小題滿分12分)已知動點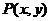 到原點的距離的平方與它到直線
到原點的距離的平方與它到直線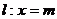 (
(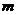 是常數)的距離相等.
是常數)的距離相等.
(1)求動點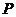 的軌跡方程
的軌跡方程 ;
(2) 就
;
(2) 就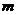 的不同取值討論方程
的不同取值討論方程 的圖形.
的圖形.
20. (本小題滿分12分)已知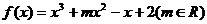 .
.
(1) 如果函數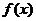 的單調遞減區間為
的單調遞減區間為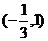 ,求函數
,求函數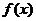 的解析式;
(2)若
的解析式;
(2)若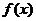 的導函數為
的導函數為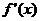 ,對任意
,對任意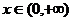 ,不等式
,不等式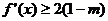 恒成立,求實數
恒成立,求實數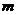 的取值范圍.
的取值范圍.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com