
3.一個口袋中裝有大小相同的2個白球和3個黑球,從中摸出一個球,放回后再摸出一個球,則兩次摸出的球恰好顏色不同的概率為________.
2.一批產品共10件,其中有兩件次品,現隨機地抽取5件,則所取5件中至多有一件次品的概率為 ( )
A.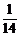 B.
B. C.
C. D.
D.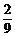
[填空題]
1.從裝有2個紅球和2個白球的口袋內任取2個球,那么互斥而不對立的兩個事件是 ( )
A.至少有1個白球,都是紅球 B.至少有1個白球,至多有1個紅球
C.恰有1個白球,恰有2個白球 D.至多有1個白球,都是紅球
4.求較復雜事件概率的方法:
(1)將所求事件的概率化為彼此互斥的事件的概率分類計算,再求和;
(2)先求對立事件的概率,再利用公式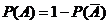

同步練習 10.6 互斥事件有一個發生的概率
[選擇題]
1.互斥事件、對立事件的確定和計算;
[例1]某單位組織4個部門的職工旅游,規定每個部門只能在3個景區中任選一個,假設各部門選擇每個景區是等可能的.
(Ⅰ)求3個景區都有部門選擇的概率;
(Ⅱ)求恰有2個景區有部門選擇的概率.
解:某單位的4個部門選擇3個景區可能出現的結果數為34.由于是任意選擇,這些結果出現的可能性都相等.
(I)3個景區都有部門選擇可能出現的結果數為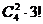 (從4個部門中任選2個作為1組,另外2個部門各作為1組,共3組,共有
(從4個部門中任選2個作為1組,另外2個部門各作為1組,共3組,共有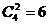 種分法,每組選擇不同的景區,共有3!種選法),記“3個景區都有部門選擇”為事件A1,那么事件A1的概率為
種分法,每組選擇不同的景區,共有3!種選法),記“3個景區都有部門選擇”為事件A1,那么事件A1的概率為
P(A1)=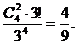
(II)解法一:分別記“恰有2個景區有部門選擇”和“4個部門都選擇同一個景區”為事件A2和A3,則事件A3的概率為P(A3)=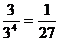 ,事件A2的概率為
,事件A2的概率為
P(A2)=1-P(A1)-P(A3)=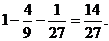
解法二:恰有2個景區有部門選擇可能的結果為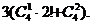 (先從3個景區任意選定2個,共有
(先從3個景區任意選定2個,共有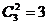 種選法,再讓4個部門來選擇這2個景區,分兩種情況:第一種情況,從4個部門中任取1個作為1組,另外3個部門作為1組,共2組,每組選擇2個不同的景區,共有
種選法,再讓4個部門來選擇這2個景區,分兩種情況:第一種情況,從4個部門中任取1個作為1組,另外3個部門作為1組,共2組,每組選擇2個不同的景區,共有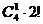 種不同選法.第二種情況,從4個部門中任選2個部門到1個景區,另外2個部門在另1個景區,共有
種不同選法.第二種情況,從4個部門中任選2個部門到1個景區,另外2個部門在另1個景區,共有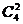 種不同選法).所以
種不同選法).所以
P(A2)=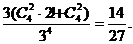
[例2]今有標號為1,2,3,4,5的五封信,另有同樣標號的五個信封.現將五封信任意地裝入五個信封,每個信封裝入一封信,試求
(1) 至少有兩封信配對的概率.
(2) 至少有一封信配對的概率
(3) 沒有一封信配對.
解:(1)設恰有兩封信配對為事件A,恰有三封信配對為事件B,恰有四封信(也即五封信配對)為事件C,則“至少有兩封信配對”事件等于A+B+C,且A、B、C兩兩互斥.
∵P(A)=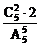 ,P(B)=
,P(B)=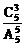 ,P(C)=
,P(C)=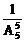 ,
,
∴所求概率P(A)+P(B)+P(C)=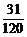 .
.
即至少有兩封信配對的概率是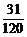 .
.
(2)恰有四封信不配對的裝法有C51(3×3)種,
∴至少有一封信配對的概率為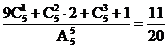 .
.
(3) 1-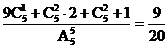 .
.
◆提煉方法:1.靈活運用事件的互斥與對立關系,進行分類計算,或間接計算.
2.恰有四封信不配對的算法.
[例3] 學校文藝隊每個隊員唱歌、跳舞至少會一門,已知會唱歌的有5人,會跳舞的有7人,現從中選3人,且至少要有一位既會唱歌又會跳舞的概率是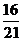 ,問該隊有多少人?
,問該隊有多少人?
解:設該隊既會唱歌又會跳舞的有x人,從而只會唱歌或只會跳舞的有(12-x)人,記“至少要有一位既會唱歌又會跳舞”的事件為A,則事件A的對立事件 是“只會唱歌或只會跳舞”
是“只會唱歌或只會跳舞”
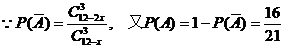
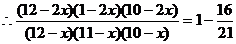
解得x=3, 12-x=9,故該隊共有9人
[例4]在袋中裝20個小球,其中彩球有n個紅色、5個藍色、10個黃色,其余為白球.
求:(1)如果從袋中取出3個都是相同顏色彩球(無白色)的概率是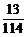 ,且n≥2,那么,袋中的紅球共有幾個?
,且n≥2,那么,袋中的紅球共有幾個?
(2)根據(1)的結論,計算從袋中任取3個小球至少有一個是紅球的概率.
解:(1)取3個球的種數為C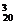 =1140.
=1140.
設“3個球全為紅色”為事件A,“3個球全為藍色”為事件B,“3個球全為黃色”為事件C.
P(B)=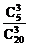 =
=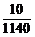 ,P(C)=
,P(C)=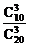 =
=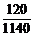 .
.
∵A、B、C為互斥事件,
∴P(A+B+C)=P(A)+P(B)+P(C),
即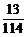 =P(A)+
=P(A)+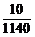 +
+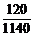
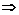 P(A)=0
P(A)=0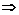 取3個球全為紅球的個數≤2.
取3個球全為紅球的個數≤2.
又∵n≥2,故n=2.
(2)記“3個球中至少有一個是紅球”為事件D.則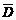 為“3個球中沒有紅球”.
為“3個球中沒有紅球”.
P(D)=1-P(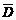 )=1-
)=1-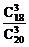 =
=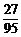 或
或
P(D)=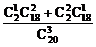 =
=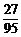 .
.
[研討.欣賞]有人玩擲硬幣走跳棋的游戲,已知硬幣出現正反面為等可能性事件,棋盤上標有第0站,第1站,第2站,…,第100站,一枚棋子開始在第0站,棋手每擲一次硬幣,棋子向前跳動一次,若擲出正面,棋向前跳一站(從k到k+1),若擲出反面,棋向前跳兩站(從k到k+2),直到棋子跳到第99站(勝利大本營)或跳到第100站(失敗集中營)時,該游戲結束.設棋子跳到第n站概率為Pn.
(1)求P0,P1,P2的值;
(2)求證:Pn-Pn-1=- (Pn-1-Pn-2),其中n∈N,2≤n≤99;
(Pn-1-Pn-2),其中n∈N,2≤n≤99;
(3)求P99及P100的值.
(1)解:棋子開始在第0站為必然事件,∴P0=1.
第一次擲硬幣出現正面,棋子跳到第1站,其概率為 ,
,
∴P1= .棋子跳到第2站應從如下兩方面考慮:
.棋子跳到第2站應從如下兩方面考慮:
①前兩次擲硬幣都出現正面,其概率為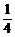 ;
;
②第一次擲硬幣出現反面,其概率為 .
.
∴P2=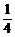 +
+ =
=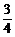 .
.
(2)證明:棋子跳到第n(2≤n≤99)站的情況是下列兩種,而且也只有兩種:
①棋子先到第n-2站,又擲出反面,其概率為 Pn-2;
Pn-2;
②棋子先到第n-1站,又擲出正面,其概率為 Pn-1.
Pn-1.
∴Pn= Pn-2+
Pn-2+ Pn-1. ∴Pn-Pn-1=-
Pn-1. ∴Pn-Pn-1=- (Pn-1-Pn-2).
(Pn-1-Pn-2).
(3)解:由(2)知,當1≤n≤99時,數列{Pn-Pn-1}是首項為P1-P0=- ,公比為-
,公比為- 的等比數列.
的等比數列.
∴P1-1=- ,P2-P1=(-
,P2-P1=(- )2,
)2,
P3-P2=(- )3,…,Pn-Pn-1=(-
)3,…,Pn-Pn-1=(- )n.
)n.
以上各式相加,得Pn-1=(- )+(-
)+(- )2+…+(-
)2+…+(- )n,
)n,
∴Pn=1+(- )+(-
)+(- )2+…+(-
)2+…+(- )n
)n
=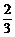 [1-(-
[1-(- )n+1](n=0,1,2,…,99).
)n+1](n=0,1,2,…,99).
∴P99=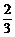 [1-(
[1-( )100],
)100],
P100= P98=
P98= ·
·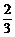 [1-(-
[1-(- )99]=
)99]=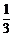 [1+(
[1+( )99].
)99].
◆提煉方法:求某些稍復雜的事件的概率時,通常有兩種方法:一是將所求事件的概率化成一些彼此互斥的事件的概率的和;二是先去求此事件的對立事件的概率.
5.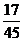 ; 6.
; 6. 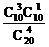 +
+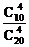 =
=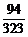 .
.
4.甲不輸即為甲獲勝或甲、乙二人下成和棋,90%=40%+p,∴p=50%.
6.一盒中裝有20個大小相同的彈子球,其中紅球10個,白球6個,黃球4個,一小孩隨手拿出4個,求至少有3個紅球的概率為________.
簡答:1-4.DADD; 2.共有56個三角形, ; 3. 不出現6點向上的概率:
; 3. 不出現6點向上的概率: =
= ,至少出現一次6點向上的概率:1-
,至少出現一次6點向上的概率:1- =
= 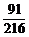 ;
;
5.若10把鑰匙中只有2把能打開某鎖,則從中任取2把能將該鎖打開的概率為 .
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com