
3.比較下列各組值的大小:
(1)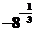 和-
和-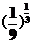 ;
;
(2) 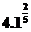 、
、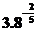 (
(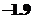 )
)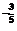
(3)0.20.5和0.40.3.
解:比較冪值的大小,一般可以借助冪函數和指數函數的單調性,有時也要借助中間值.
 (1)由于冪函數
(1)由于冪函數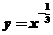 在(0,+∞)上是減函數,
在(0,+∞)上是減函數,
所以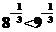 ,因此
,因此 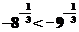 ,
,
即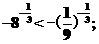
(2)由于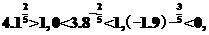
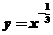
因此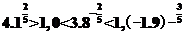
(3)由于指數函數y=0.2x在R上是減函數,
所以0.20.5<0.20.3,
又由于冪函數y=x0.3在(0,+∞)上是增函數,
所以0.20.3<0.40.3,故有0.20.5<0.40.3.
|
題組二 |
二次函數的解析式 |
2.函數y=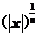 (n∈N,n>2)的圖象的大致形狀是
( )
(n∈N,n>2)的圖象的大致形狀是
( )
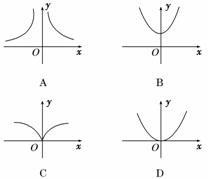
解析:由n>2知-<0,
∴x≠0,且圖象在第一象限內為減函數.
答案:A
1.已知冪函數f(x)=xα的部分對應值如下表:
|
x |
1 |
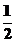
|
|
f(x) |
1 |
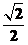 |
則不等式f(|x|)≤2的解集是 ( )
A.{x|-4≤x≤4} B.{x|0≤x≤4} C.{x|-≤x≤} D.{x|0<x≤}
解析:由表知=()α,∴α=,∴f(x)=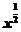 .
.
∴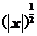 ≤2,即|x|≤4,故-4≤x≤4.
≤2,即|x|≤4,故-4≤x≤4.
答案:A
20.(16分)設函數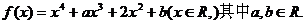
(1)當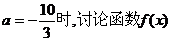 的單調性;
的單調性;
(2)若函數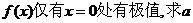 的取值范圍;
的取值范圍;
(3)若對于任意的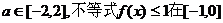 上恒成立,求
上恒成立,求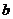 的取值范圍.
的取值范圍.
19.(16分)已知函數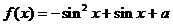 ,若
,若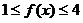 對一切
對一切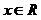
恒成立.求實數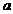 的取值范圍.
的取值范圍.
18.(15分) 某廠生產某種產品的年固定成本為250萬元,每生產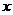 千件,需另投入成本為
千件,需另投入成本為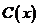 ,當年產量不足80千件時,
,當年產量不足80千件時,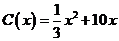 (萬元);當年產量不小于80千件時,
(萬元);當年產量不小于80千件時,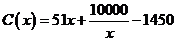 (萬元).通過市場分析,若每件售價為500元時,該廠年內生產的商品能全部售完.
(萬元).通過市場分析,若每件售價為500元時,該廠年內生產的商品能全部售完.
(1)寫出年利潤L(萬元)關于年產量x (千件)的函數解析式.
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
17.(15分)已知二次函數f(x)滿足:①在x=1時有極值;②圖象過點(0,-3),且在該點處的切線與直線2x+y=0平行.
⑴求f(x)的解析式;
⑵求函數g(x)=f(x2)的單調遞增區間.
16.(14分)已知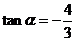 ,求:(1)
,求:(1)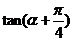 的值;
的值;
(2) 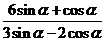 的值;(3)
的值;(3)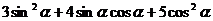 的值.
的值.
15.(14分) 已知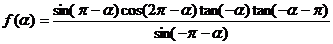
(1)化簡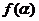 .
.
(2)若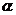 是第三象限角,且
是第三象限角,且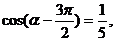 求
求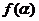 的值.
的值.
14.給出下列四個結論:
①命題“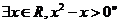 的否定是“
的否定是“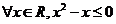 ”;
”;
②“若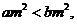 則
則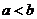 ”的逆命題為真;
”的逆命題為真;
③函數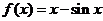 (x
(x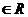 )有3個零點;
)有3個零點;
④對于任意實數x,有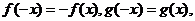
且x>0時,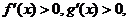 則x<0時
則x<0時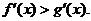
其中正確結論的序號是 .(填上所有正確結論的序號)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com