
19、答案:(1)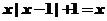 所以
所以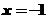 或
或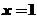 ;
;
(2)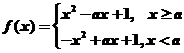 ,
,
1O.當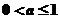 時,
時,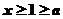 ,這時,
,這時,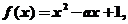 對稱軸
對稱軸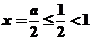 ,
,
所以函數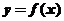 在區間
在區間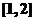 上遞增,
上遞增,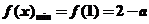 ;
;
2O.當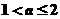 時,
時,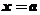 時函數
時函數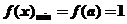 ;
;
3O. 當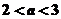 時,
時,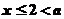 ,這時,
,這時,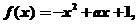 對稱軸
對稱軸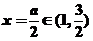 ,
,
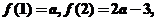
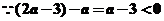
所以函數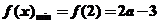 ;
;
(3)因為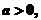 所以
所以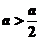 ,
,
所以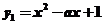 在
在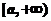 上遞增;
上遞增;
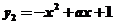 在
在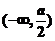 遞增,在
遞增,在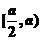 上遞減.
上遞減.
因為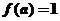 ,所以當
,所以當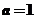 時,函數
時,函數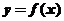 的圖像與直線
的圖像與直線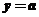 有2個交點;
有2個交點;
又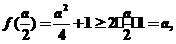 當且僅當
當且僅當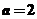 時,等號成立.
時,等號成立.
所以,當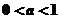 時,函數
時,函數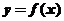 的圖像與直線
的圖像與直線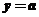 有1個交點;
有1個交點;
當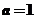 時,函數
時,函數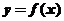 的圖像與直線
的圖像與直線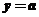 有2個交點;
有2個交點;
當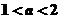 時,函數
時,函數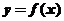 的圖像與直線
的圖像與直線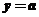 有3個交點;
有3個交點;
當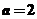 時,函數
時,函數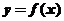 的圖像與直線
的圖像與直線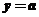 有2個交點;
有2個交點;
當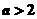 時,函數
時,函數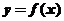 的圖像與直線
的圖像與直線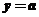 有3個交點.
有3個交點.
18、(1)由圖像關于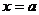 對稱得
對稱得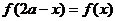 ,即
,即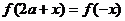 ,2分
,2分
因為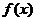 為偶函數,所以
為偶函數,所以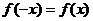 ,從而
,從而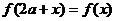 ,所以
,所以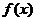 是以
是以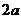 為周期的函數. 2分
為周期的函數. 2分
(2)若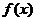 為奇函數,則圖像關于原點對稱,
為奇函數,則圖像關于原點對稱,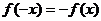 , 2分
, 2分
由條件得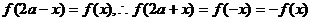 ,所以
,所以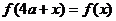 ,
,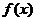 是以
是以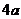 為周期的函數. 2分
為周期的函數. 2分
(3)(本小題評分說明:下面解答給出的是滿分結論,如果是關于點或直線的部分推廣,應視解答程度適當給分,具體標準結合考生答題情況制訂細則。但是沒有把握推廣的內涵,以至于沒有給出推廣意義下的真命題,或寫出的命題不是真命題。這類答卷在寫出一個真命題、并予以證明中,應得0分。)
推廣:若函數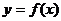 圖像關于點
圖像關于點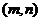 對稱且關于直線
對稱且關于直線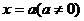 對稱,則函數
對稱,則函數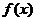 是以
是以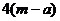 為周期的周期函數.3分
為周期的周期函數.3分
由條件圖像關于點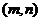 對稱,故
對稱,故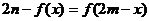 ,又圖像關于直線
,又圖像關于直線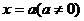 對稱,
對稱,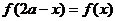 ,所以
,所以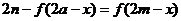 ,即
,即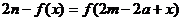 .2分
.2分
當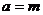 時,
時,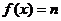 為常值函數,是周期函數.
為常值函數,是周期函數.
當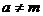 時,由
時,由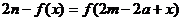 得
得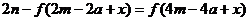
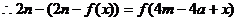 ,因此
,因此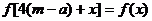 ,
,
所以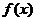 是以
是以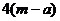 為周期的函數.2分
為周期的函數.2分
17、解:(1)因為2002年底剛達到小康,所以n=50% …………1分
且2002年每戶家庭消費支出總額為9600元,
故食品消費支出總額為9600×50%=4800元 …………2分
則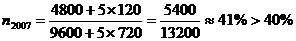 ,即2007年底能達到富裕。
,即2007年底能達到富裕。
…………6分
(2)設2002年的消費支出總額為a元,則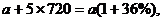
從而求得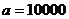 元,
…………8分
元,
…………8分
又設其中食品消費支出總額為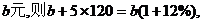
從而求得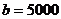 元。 …………10分
元。 …………10分
當恩格爾系數為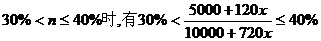 ,
,
解得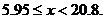 …………13分
…………13分
則6年后即2008年底起達到富裕。 …………15分
16、(1)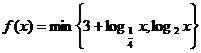 =
=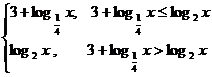 3分
3分
解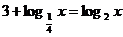 得
得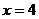 .又函數
.又函數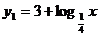 在
在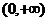 內遞減,
內遞減,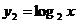 在
在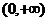 內遞增,所以當
內遞增,所以當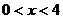 時,
時,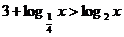 ;當
;當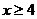 時,
時,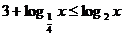 . 4分
. 4分
所以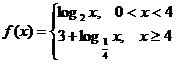 . 1分
. 1分
(2)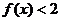 等價于:
等價于: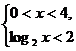 ①或
①或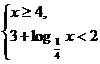 ②. 3分
②. 3分
解得: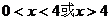 ,即
,即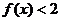 的解集為
的解集為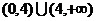 .3分
.3分
15、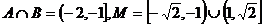
12、0或-2 13、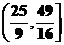 14、
14、 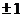 和1
和1
6、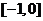 7、
7、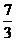 8、
8、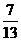 9、
9、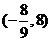 10、
10、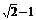 11、
11、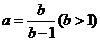
1、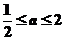 2、
2、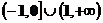 3、
3、 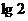 ;4、
;4、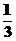 5、
5、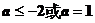
20、(本小題滿分16分)
定義在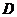 上的函數
上的函數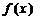 ,如果滿足:對任意
,如果滿足:對任意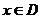 ,存在常數
,存在常數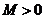 ,都有
,都有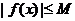 成立,則稱
成立,則稱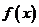 是
是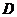 上的有界函數,其中
上的有界函數,其中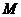 稱為函數
稱為函數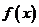 的上界.
的上界.
已知函數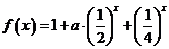 ;
;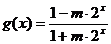 .
.
(1)當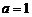 時,求函數
時,求函數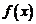 在
在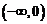 上的值域,并判斷函數
上的值域,并判斷函數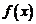 在
在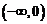 上是否為有界函數,請說明理由;
上是否為有界函數,請說明理由;
(2)若函數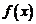 在
在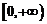 上是以3為上界的有界函數,求實數
上是以3為上界的有界函數,求實數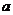 的取值范圍;
的取值范圍;
(3)若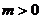 ,函數
,函數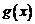 在
在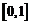 上的上界是
上的上界是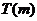 ,求
,求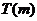 的取值范圍.
的取值范圍.
2011屆常州北郊中學高三學情分析(二)2010.9
19、(本小題滿分16分)
已知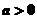 ,函數
,函數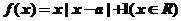 .
.
(1)當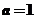 時,求所有使
時,求所有使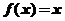 成立的
成立的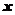 的值;
的值;
(2)當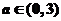 時,求函數
時,求函數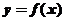 在閉區間
在閉區間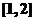 上的最小值;
上的最小值;
(3)試討論函數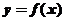 的圖像與直線
的圖像與直線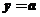 的交點個數.
的交點個數.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com