
8、設全集U={2,3,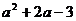 },A={b,2},
},A={b,2},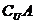 ={b,2},求實數a和b的值.
={b,2},求實數a和b的值.
(a=2、-4,b=3)
7、設全集U(U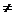 Φ),已知集合M,N,P,且M=CUN,N=CUP,則M與P的關系是( )
Φ),已知集合M,N,P,且M=CUN,N=CUP,則M與P的關系是( )
(A) M=CUP,(B)M=P,(C)M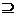 P,(D)M
P,(D)M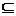 P.
P.
解:選B.
6、集合U={(x,y)|x∈{1,2},y∈{1,2}} ,
A={(x,y)|x∈N*,y∈N*,x+y=3},求CUA.
解:CUA={(1,1),(2,2)}.
5、已知U=R,A={x|x2+3x+2<0}, 求CUA.
解:CUA={x|x≤-2,或x≥-1}.
4、設U={梯形},A={等腰梯形},求CUA.
解:CUA={不等腰梯形}.
3、已知全集U,A是U的子集,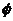 是空集,B=CUA,求CUB,CU
是空集,B=CUA,求CUB,CU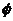 ,CUU
,CUU
(CUB= CU(CUA,CU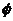 =U,CUU=
=U,CUU=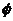 )
)
2、已知全集U={2,4,1-a},A={2,a2-a+2} 如果CUA=
如果CUA=
{-1},那么a的值為 2 
1、已知全集U={x|-1<x<9},A={x|1<x<a},若A≠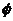 ,則a的取值范圍是
(D)
,則a的取值范圍是
(D)
(A)a<9 (B)a≤9 (C)a≥9 (D)1<a≤9
3、全集:如果集合S含有我們所要研究的各個集合的全部元素,這個集合就可以看作一個全集,全集通常用U表示
三講解范例:
例1(1)若S={1,2,3,4,5,6},A={1,3,5},求CSA
(2)若A={0},求證:CNA=N*
 (3)求證:CRQ是無理數集
(3)求證:CRQ是無理數集
解(1)∵S={1,2,3,4,5,6},A={1,3,5},
∴由補集的定義得CSA={2,4,6}
證明(2)∵A={0},N={0,1,2,3,4,…},N*={1,2,3,4,…}
∴由補集的定義得CNA=N*
證明(3)∵ Q是有理數集合,R是實數集合
∴由補集的定義得CRQ是無理數集合
例2已知全集U=R,集合A={x|1≤2x+1<9},求C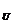 A
A
解:∵A={x|1≤2x+1<9}={x|0≤X<4},U=R



 0 4 x
0 4 x
∴C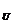 A={x|x<0,或x≥4}
A={x|x<0,或x≥4}
例3 已知S={x|-1≤x+2<8},A={x|-2<1-x≤1},
B={x|5<2x-1<11},討論A與C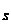 B的關系
B的關系
解:∵S={x|-3≤x<6},A={x|0≤x<3}, B={x|3≤x<6}
∴C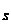 B={x|-3≤x<3}
B={x|-3≤x<3}
∴A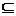 C
C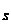 B
B
全集與補集
1 補集:一般地,設S是一個集合,A是S的一個子集(即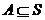 ),
),
由S中所有不屬于A的元素組成的集合,叫做S中子集A
 的補集(或余集),記作
的補集(或余集),記作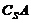 ,即
,即
CSA=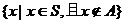
2、性質:CS(CSA)=A ,CSS=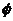 ,CS
,CS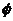 =S
=S
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com