
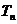 =
=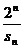 =
=

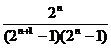 =
=
 (
(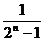 -
-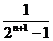 ) .
) .
=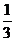
 (
( -1)
-1)  (
( -2) =
-2) =
 (
( -1)
-1)  (
( -1).
-1).
將 =
=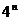 -
- 代入(1)得:
代入(1)得: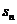 =
=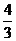
 (
(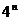 -
- )-
)-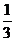

 +
+
(Ⅱ)解本問可先求出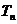 =
=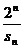 =
=

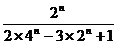 , 欲證數列不等式
, 欲證數列不等式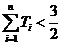 ,常規的方法有四種,即求和分析法,數學歸納法,利用數列單調性法,放縮法.對于本題來說,由于不等式左邊是n的遞增式,右邊是常數,利用數列單調性法證左邊式子的最大值小于
,常規的方法有四種,即求和分析法,數學歸納法,利用數列單調性法,放縮法.對于本題來說,由于不等式左邊是n的遞增式,右邊是常數,利用數列單調性法證左邊式子的最大值小于 是不可能的;同樣由于n=k時比n=k+1左邊式子要小,故不可利用數學歸納法求解;由于
是不可能的;同樣由于n=k時比n=k+1左邊式子要小,故不可利用數學歸納法求解;由于 是
是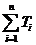 在
在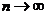 時的極限(可求和證明),故不適于利用放縮法進行,最直接的方法是求和分析法,這也是證明數列不等式最常規的方法,也是最先考慮的方法. 由于
時的極限(可求和證明),故不適于利用放縮法進行,最直接的方法是求和分析法,這也是證明數列不等式最常規的方法,也是最先考慮的方法. 由于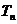 是分式形式,可考慮裂項求和法,把
是分式形式,可考慮裂項求和法,把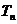 變形為
變形為

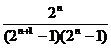 進而轉化為
進而轉化為
 (
(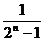 -
-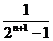 ) ,則問題迎刃而解.具體解法如下:
) ,則問題迎刃而解.具體解法如下:
綜上,對任意正整數n,都有 =
=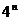 -
- .
.
得 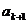 =
=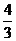 (
(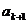 -
- 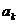 )-
)-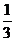

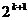 ,
, 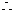
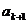 =4
=4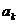 +
+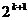 =4(
=4(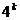 -
-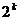 )+
)+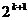 =
=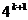 -
-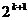 .
.
則由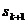 =
=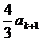 -
-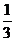

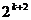 +
+ 及
及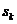 =
=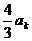 -
-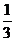

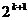 +
+ ,
,
2)假設n=k時成立,即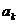 =
=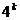 -
-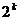 .
.
綜上,對任意正整數n,都有 =
=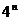 -
- .
.
另:用數學歸納法也可類似處理:
1)當n=1時,顯然成立.
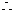 當n=k+1時也成立.
當n=k+1時也成立.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com