
12. 函數的對稱性。
①滿足條件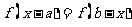 的函數的圖象關于直線
的函數的圖象關于直線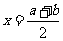 對稱。如已知二次函數
對稱。如已知二次函數 滿足條件
滿足條件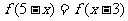 且方程
且方程 有等根,則
有等根,則 =_____(答:
=_____(答: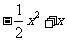 );
);
②點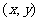 關于
關于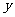 軸的對稱點為
軸的對稱點為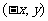 ;函數
;函數 關于
關于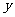 軸的對稱曲線方程為
軸的對稱曲線方程為 ;
;
③點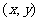 關于
關于 軸的對稱點為
軸的對稱點為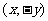 ;函數
;函數 關于
關于 軸的對稱曲線方程為
軸的對稱曲線方程為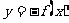 ;
;
④點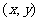 關于原點的對稱點為
關于原點的對稱點為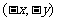 ;函數
;函數 關于原點的對稱曲線方程為
關于原點的對稱曲線方程為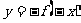 ;
;
⑤點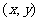 關于直線
關于直線 的對稱點為
的對稱點為 ;曲線
;曲線 關于直線
關于直線 的對稱曲線的方程為
的對稱曲線的方程為 。特別地,點
。特別地,點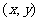 關于直線
關于直線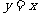 的對稱點為
的對稱點為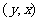 ;曲線
;曲線 關于直線
關于直線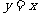 的對稱曲線的方程為
的對稱曲線的方程為
 ;點
;點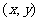 關于直線
關于直線 的對稱點為
的對稱點為 ;曲線
;曲線 關于直線
關于直線 的對稱曲線的方程為
的對稱曲線的方程為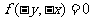 。如己知函數
。如己知函數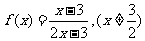 ,若
,若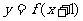 的圖像是
的圖像是 ,它關于直線
,它關于直線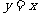 對稱圖像是
對稱圖像是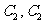 關于原點對稱的圖像為
關于原點對稱的圖像為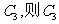 對應的函數解析式是___________(答:
對應的函數解析式是___________(答: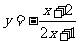 );
);
⑥曲線 關于點
關于點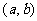 的對稱曲線的方程為
的對稱曲線的方程為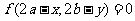 。如若函數
。如若函數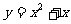 與
與 的圖象關于點(-2,3)對稱,則
的圖象關于點(-2,3)對稱,則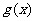 =______(答:
=______(答: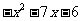 )
)
⑦形如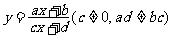 的圖像是雙曲線,其兩漸近線分別直線
的圖像是雙曲線,其兩漸近線分別直線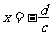
(由分母為零確定)和直線 (由分子、分母中
(由分子、分母中 的系數確定),對稱中心是點
的系數確定),對稱中心是點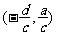 。如已知函數圖象
。如已知函數圖象 與
與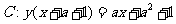 關于直線
關于直線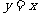 對稱,且圖象
對稱,且圖象 關于點(2,-3)對稱,則a的值為______(答:2)
關于點(2,-3)對稱,則a的值為______(答:2)
⑧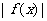 的圖象先保留
的圖象先保留 原來在
原來在 軸上方的圖象,作出
軸上方的圖象,作出 軸下方的圖象關于
軸下方的圖象關于 軸的對稱圖形,然后擦去
軸的對稱圖形,然后擦去 軸下方的圖象得到;
軸下方的圖象得到;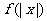 的圖象先保留
的圖象先保留 在
在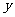 軸右方的圖象,擦去
軸右方的圖象,擦去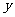 軸左方的圖象,然后作出
軸左方的圖象,然后作出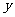 軸右方的圖象關于
軸右方的圖象關于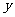 軸的對稱圖形得到。如(1)作出函數
軸的對稱圖形得到。如(1)作出函數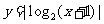 及
及 的圖象;(2)若函數
的圖象;(2)若函數 是定義在R上的奇函數,則函數
是定義在R上的奇函數,則函數 的圖象關于____對稱 (答:
的圖象關于____對稱 (答: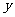 軸)
軸)
提醒:(1)從結論②③④⑤⑥可看出,求對稱曲線方程的問題,實質上是利用代入法轉化為求點的對稱問題;(2)證明函數圖像的對稱性,即證明圖像上任一點關于對稱中心(對稱軸)的對稱點仍在圖像上;(3)證明圖像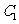 與
與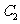 的對稱性,需證兩方面:①證明
的對稱性,需證兩方面:①證明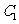 上任意點關于對稱中心(對稱軸)的對稱點仍在
上任意點關于對稱中心(對稱軸)的對稱點仍在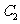 上;②證明
上;②證明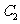 上任意點關于對稱中心(對稱軸)的對稱點仍在
上任意點關于對稱中心(對稱軸)的對稱點仍在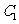 上。如(1)已知函數
上。如(1)已知函數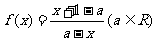 。求證:函數
。求證:函數 的圖像關于點
的圖像關于點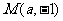 成中心對稱圖形;(2)設曲線C的方程是
成中心對稱圖形;(2)設曲線C的方程是 ,將C沿
,將C沿 軸,
軸,  軸正方向分別平行移動
軸正方向分別平行移動 單位長度后得曲線
單位長度后得曲線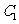 。①寫出曲線
。①寫出曲線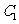 的方程(答:
的方程(答: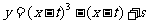 );②證明曲線C與
);②證明曲線C與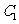 關于點
關于點 對稱。
對稱。
11. 常見的圖象變換
①函數
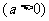 的圖象是把函數
的圖象是把函數 的圖象沿
的圖象沿 軸向左平移
軸向左平移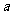 個單位得到的。如設
個單位得到的。如設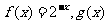 的圖像與
的圖像與 的圖像關于直線
的圖像關于直線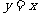 對稱,
對稱,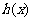 的圖像由
的圖像由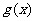 的圖像向右平移1個單位得到,則
的圖像向右平移1個單位得到,則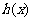 為__________(答:
為__________(答: 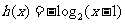 )
)
②函數 (
(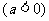 的圖象是把函數
的圖象是把函數 的圖象沿
的圖象沿 軸向右平移
軸向右平移 個單位得到的。如(1)若
個單位得到的。如(1)若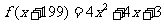 ,則函數
,則函數 的最小值為____(答:2);(2)要得到
的最小值為____(答:2);(2)要得到 的圖像,只需作
的圖像,只需作 關于_____軸對稱的圖像,再向____平移3個單位而得到(答:
關于_____軸對稱的圖像,再向____平移3個單位而得到(答: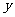 ;右);(3)函數
;右);(3)函數 的圖象與
的圖象與 軸的交點個數有____個(答:2)
軸的交點個數有____個(答:2)
③函數 +
+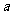
 的圖象是把函數
的圖象是把函數 助圖象沿
助圖象沿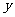 軸向上平移
軸向上平移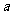 個單位得到的;
個單位得到的;
④函數 +
+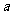
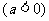 的圖象是把函數
的圖象是把函數 助圖象沿
助圖象沿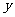 軸向下平移
軸向下平移 個單位得到的;如將函數
個單位得到的;如將函數 的圖象向右平移2個單位后又向下平移2個單位,所得圖象如果與原圖象關于直線
的圖象向右平移2個單位后又向下平移2個單位,所得圖象如果與原圖象關于直線 對稱,那么
對稱,那么 
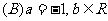
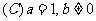
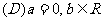 (答:C)
(答:C)
⑤函數
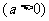 的圖象是把函數
的圖象是把函數 的圖象沿
的圖象沿 軸伸縮為原來的
軸伸縮為原來的 得到的。如(1)將函數
得到的。如(1)將函數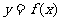 的圖像上所有點的橫坐標變為原來的
的圖像上所有點的橫坐標變為原來的 (縱坐標不變),再將此圖像沿
(縱坐標不變),再將此圖像沿 軸方向向左平移2個單位,所得圖像對應的函數為_____(答:
軸方向向左平移2個單位,所得圖像對應的函數為_____(答: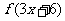 );(2)如若函數
);(2)如若函數 是偶函數,則函數
是偶函數,則函數 的對稱軸方程是_______(答:
的對稱軸方程是_______(答: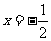 ).
).
⑥函數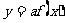
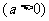 的圖象是把函數
的圖象是把函數 的圖象沿
的圖象沿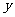 軸伸縮為原來的
軸伸縮為原來的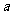 倍得到的.
倍得到的.
10.函數的單調性。
(1)確定函數的單調性或單調區間的常用方法:
①在解答題中常用:定義法(取值--作差--變形--定號)、導數法(在區間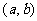 內,若總有
內,若總有 ,則
,則 為增函數;反之,若
為增函數;反之,若 在區間
在區間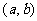 內為增函數,則
內為增函數,則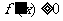 ,請注意兩者的區別所在。如已知函數
,請注意兩者的區別所在。如已知函數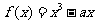 在區間
在區間 上是增函數,則
上是增函數,則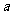 的取值范圍是____(答:
的取值范圍是____(答: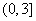 ));
));
②在選擇填空題中還可用數形結合法、特殊值法等等,特別要注意
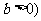 型函數的圖象和單調性在解題中的運用:增區間為
型函數的圖象和單調性在解題中的運用:增區間為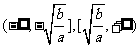 ,減區間為
,減區間為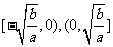 .如(1)若函數
.如(1)若函數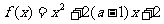 在區間(-∞,4] 上是減函數,那么實數
在區間(-∞,4] 上是減函數,那么實數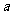 的取值范圍是______(答:
的取值范圍是______(答: ));(2)已知函數
));(2)已知函數 在區間
在區間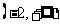 上為增函數,則實數
上為增函數,則實數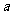 的取值范圍_____(答:
的取值范圍_____(答: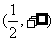 );(3)若函數
);(3)若函數 的值域為R,則實數
的值域為R,則實數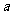 的取值范圍是______(答:
的取值范圍是______(答: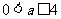 且
且 ));
));
③復合函數法:復合函數單調性的特點是同增異減,如函數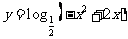 的單調遞增區間是________(答:(1,2))。
的單調遞增區間是________(答:(1,2))。
(2)特別提醒:求單調區間時,一是勿忘定義域,如若函數 在區間
在區間 上為減函數,求
上為減函數,求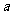 的取值范圍(答:
的取值范圍(答: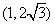 );二是在多個單調區間之間不一定能添加符號“
);二是在多個單調區間之間不一定能添加符號“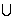 ”和“或”;三是單調區間應該用區間表示,不能用集合或不等式表示.
”和“或”;三是單調區間應該用區間表示,不能用集合或不等式表示.
(3)你注意到函數單調性與奇偶性的逆用了嗎?(①比較大小;②解不等式;③求參數范圍).如已知奇函數 是定義在
是定義在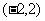 上的減函數,若
上的減函數,若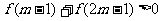 ,求實數
,求實數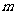 的取值范圍。(答:
的取值范圍。(答: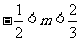 )
)
9.函數的奇偶性。
(1)具有奇偶性的函數的定義域的特征:定義域必須關于原點對稱!為此確定函數的奇偶性時,務必先判定函數定義域是否關于原點對稱。如若函數
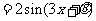 ,
,
 為奇函數,其中
為奇函數,其中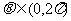 ,則
,則 的值是 (答:0);
的值是 (答:0);
(2)確定函數奇偶性的常用方法(若所給函數的解析式較為復雜,應先化簡,再判斷其奇偶性):
①定義法:如判斷函數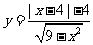 的奇偶性____(答:奇函數)。
的奇偶性____(答:奇函數)。
②利用函數奇偶性定義的等價形式: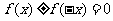 或
或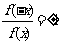 (
( )。如判斷
)。如判斷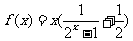 的奇偶性___.(答:偶函數)
的奇偶性___.(答:偶函數)
③圖像法:奇函數的圖象關于原點對稱;偶函數的圖象關于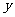 軸對稱。
軸對稱。
(3)函數奇偶性的性質:
①奇函數在關于原點對稱的區間上若有單調性,則其單調性完全相同;偶函數在關于原點對稱的區間上若有單調性,則其單調性恰恰相反.
②如果奇函數有反函數,那么其反函數一定還是奇函數.
③若 為偶函數,則
為偶函數,則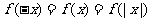 .如若定義在R上的偶函數
.如若定義在R上的偶函數 在
在 上是減函數,且
上是減函數,且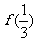 =2,則不等式
=2,則不等式 的解集為______.(答:
的解集為______.(答: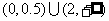 )
)
④若奇函數 定義域中含有0,則必有
定義域中含有0,則必有 .故
.故 是
是 為奇函數的既不充分也不必要條件。如若
為奇函數的既不充分也不必要條件。如若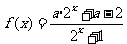 為奇函數,則實數
為奇函數,則實數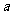 =____(答:1).
=____(答:1).
⑤定義在關于原點對稱區間上的任意一個函數,都可表示成“一個奇函數與一個偶函數的和(或差)”。如設 是定義域為R的任一函數,
是定義域為R的任一函數, 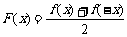 ,
,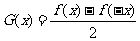 。①判斷
。①判斷 與
與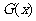 的奇偶性; ②若將函數
的奇偶性; ②若將函數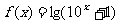 ,表示成一個奇函數
,表示成一個奇函數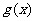 和一個偶函數
和一個偶函數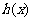 之和,則
之和,則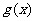 =____(答:①
=____(答:① 為偶函數,
為偶函數,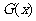 為奇函數;②
為奇函數;②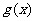 =
=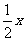 )
)
⑥復合函數的奇偶性特點是:“內偶則偶,內奇同外”.
⑦既奇又偶函數有無窮多個( ,定義域是關于原點對稱的任意一個數集).
,定義域是關于原點對稱的任意一個數集).
8. 反函數:
(1)存在反函數的條件是對于原來函數值域中的任一個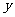 值,都有唯一的
值,都有唯一的 值與之對應,故單調函數一定存在反函數,但反之不成立;偶函數只有
值與之對應,故單調函數一定存在反函數,但反之不成立;偶函數只有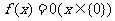 有反函數;周期函數一定不存在反函數。如函數
有反函數;周期函數一定不存在反函數。如函數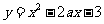 在區間[1, 2]上存在反函數的充要條件是A、
在區間[1, 2]上存在反函數的充要條件是A、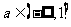 B、
B、 C、
C、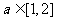 D、
D、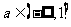
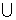
 (答:D)
(答:D)
(2)求反函數的步驟:①反求 ;②互換
;②互換  、
、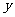 ;③注明反函數的定義域(原來函數的值域)。注意函數
;③注明反函數的定義域(原來函數的值域)。注意函數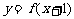 的反函數不是
的反函數不是 ,而是
,而是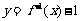 。如設
。如設 .求
.求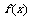 的反函數
的反函數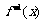 (答:
(答: ).
).
(3)反函數的性質:
①反函數的定義域是原來函數的值域,反函數的值域是原來函數的定義域。如單調遞增函數 滿足條件
滿足條件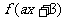 = x ,其中
= x ,其中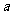 ≠ 0 ,若
≠ 0 ,若 的反函數
的反函數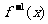 的定義域為
的定義域為 ,則
,則 的定義域是____________(答:[4,7]).
的定義域是____________(答:[4,7]).
②函數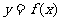 的圖象與其反函數
的圖象與其反函數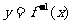 的圖象關于直線
的圖象關于直線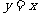 對稱,注意函數
對稱,注意函數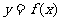 的圖象與
的圖象與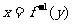 的圖象相同。如(1)已知函數
的圖象相同。如(1)已知函數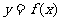 的圖象過點(1,1),那么
的圖象過點(1,1),那么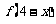 的反函數的圖象一定經過點_____(答:(1,3));(2)已知函數
的反函數的圖象一定經過點_____(答:(1,3));(2)已知函數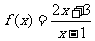 ,若函數
,若函數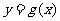 與
與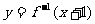 的圖象關于直線
的圖象關于直線 對稱,求
對稱,求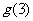 的值(答:
的值(答: );
);
③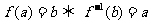 。如(1)已知函數
。如(1)已知函數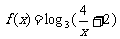 ,則方程
,則方程 的解
的解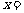 ______(答:1);(2)設函數f(x)的圖象關于點(1,2)對稱,且存在反函數
______(答:1);(2)設函數f(x)的圖象關于點(1,2)對稱,且存在反函數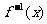 ,f (4)=0,則
,f (4)=0,則 = (答:-2)
= (答:-2)
④互為反函數的兩個函數具有相同的單調性和奇函數性。如已知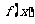 是
是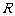 上的增函數,點
上的增函數,點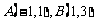 在它的圖象上,
在它的圖象上,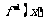 是它的反函數,那么不等式
是它的反函數,那么不等式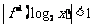 的解集為________(答:(2,8));
的解集為________(答:(2,8));
⑤設 的定義域為A,值域為B,則有
的定義域為A,值域為B,則有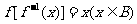 ,
,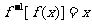
 ,但
,但 。
。
7.求函數解析式的常用方法:
(1)待定系數法--已知所求函數的類型(二次函數的表達形式有三種:一般式: ;頂點式:
;頂點式: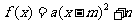 ;零點式:
;零點式: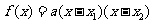 ,要會根據已知條件的特點,靈活地選用二次函數的表達形式)。如已知
,要會根據已知條件的特點,靈活地選用二次函數的表達形式)。如已知 為二次函數,且
為二次函數,且 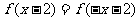 ,且f(0)=1,圖象在x軸上截得的線段長為2
,且f(0)=1,圖象在x軸上截得的線段長為2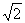 ,求
,求 的解析式 。(答:
的解析式 。(答: )
)
(2)代換(配湊)法--已知形如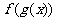 的表達式,求
的表達式,求 的表達式。如(1)已知
的表達式。如(1)已知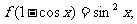 求
求 的解析式(答:
的解析式(答: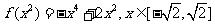 );(2)若
);(2)若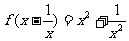 ,則函數
,則函數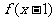 =_____(答:
=_____(答: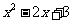 );(3)若函數
);(3)若函數 是定義在R上的奇函數,且當
是定義在R上的奇函數,且當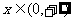 時,
時,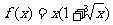 ,那么當
,那么當 時,
時, =________(答:
=________(答: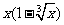 ). 這里需值得注意的是所求解析式的定義域的等價性,即
). 這里需值得注意的是所求解析式的定義域的等價性,即 的定義域應是
的定義域應是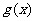 的值域。
的值域。
(3)方程的思想--已知條件是含有 及另外一個函數的等式,可抓住等式的特征對等式的進行賦值,從而得到關于
及另外一個函數的等式,可抓住等式的特征對等式的進行賦值,從而得到關于 及另外一個函數的方程組。如(1)已知
及另外一個函數的方程組。如(1)已知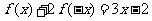 ,求
,求 的解析式(答:
的解析式(答: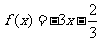 );(2)已知
);(2)已知 是奇函數,
是奇函數,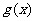 是偶函數,且
是偶函數,且 +
+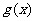 =
= 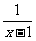 ,則
,則 = __(答:
= __(答: )。
)。
6.分段函數的概念。分段函數是在其定義域的不同子集上,分別用幾個不同的式子來表示對應關系的函數,它是一類較特殊的函數。在求分段函數的值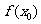 時,一定首先要判斷
時,一定首先要判斷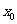 屬于定義域的哪個子集,然后再代相應的關系式;分段函數的值域應是其定義域內不同子集上各關系式的取值范圍的并集。如(1)設函數
屬于定義域的哪個子集,然后再代相應的關系式;分段函數的值域應是其定義域內不同子集上各關系式的取值范圍的并集。如(1)設函數 ,則使得
,則使得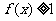 的自變量
的自變量 的取值范圍是__________(答:
的取值范圍是__________(答: );(2)已知
);(2)已知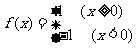 ,則不等式
,則不等式 的解集是________(答:
的解集是________(答: )
)
5.求函數值域(最值)的方法:
(1)配方法--二次函數(二次函數在給出區間上的最值有兩類:一是求閉區間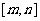 上的最值;二是求區間定(動),對稱軸動(定)的最值問題。求二次函數的最值問題,勿忘數形結合,注意“兩看”:一看開口方向;二看對稱軸與所給區間的相對位置關系),如(1)求函數
上的最值;二是求區間定(動),對稱軸動(定)的最值問題。求二次函數的最值問題,勿忘數形結合,注意“兩看”:一看開口方向;二看對稱軸與所給區間的相對位置關系),如(1)求函數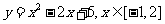 的值域(答:[4,8]);(2)當
的值域(答:[4,8]);(2)當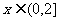 時,函數
時,函數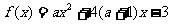 在
在 時取得最大值,則
時取得最大值,則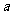 的取值范圍是___(答:
的取值范圍是___(答: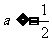 );(3)已知
);(3)已知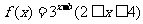 的圖象過點(2,1),則
的圖象過點(2,1),則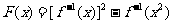 的值域為______(答:[2, 5])
的值域為______(答:[2, 5])
(2)換元法--通過換元把一個較復雜的函數變為簡單易求值域的函數,其函數特征是函數解析式含有根式或三角函數公式模型,如(1)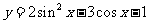 的值域為_____(答:
的值域為_____(答: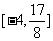 );(2)
);(2)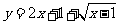 的值域為_____(答:
的值域為_____(答: )(令
)(令 ,
, 。運用換元法時,要特別要注意新元
。運用換元法時,要特別要注意新元 的范圍);(3)
的范圍);(3)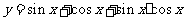 的值域為____(答:
的值域為____(答: );(4)
);(4)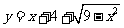 的值域為____(答:
的值域為____(答: );
);
(3)函數有界性法--直接求函數的值域困難時,可以利用已學過函數的有界性,來確定所求函數的值域,最常用的就是三角函數的有界性,如求函數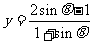 ,
, ,
,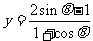 的值域(答:
的值域(答:  、(0,1)、
、(0,1)、 );
);
(4)單調性法--利用一次函數,反比例函數,指數函數,對數函數等函數的單調性,如求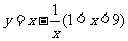 ,
,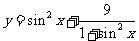 ,
, 的值域為______(答:
的值域為______(答: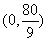 、
、 、
、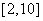 );
);
(5)數形結合法--函數解析式具有明顯的某種幾何意義,如兩點的距離、直線斜率、等等,如(1)已知點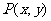 在圓
在圓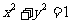 上,求
上,求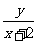 及
及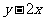 的取值范圍(答:
的取值范圍(答: 、
、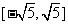 );(2)求函數
);(2)求函數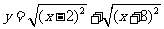 的值域(答:
的值域(答: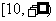 );(3)求函數
);(3)求函數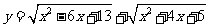 及
及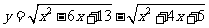 的值域(答:
的值域(答: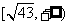 、
、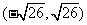 )注意:求兩點距離之和時,要將函數式變形,使兩定點在
)注意:求兩點距離之和時,要將函數式變形,使兩定點在 軸的兩側,而求兩點距離之差時,則要使兩定點在
軸的兩側,而求兩點距離之差時,則要使兩定點在 軸的同側。
軸的同側。
(6)判別式法--對分式函數(分子或分母中有一個是二次)都可通用,但這類題型有時也可以用其它方法進行求解,不必拘泥在判別式法上,也可先通過部分分式后,再利用均值不等式:
① 型,可直接用不等式性質,如求
型,可直接用不等式性質,如求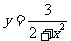 的值域(答:
的值域(答: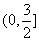 )
)
②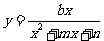 型,先化簡,再用均值不等式,如(1)求
型,先化簡,再用均值不等式,如(1)求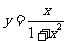 的值域(答:
的值域(答: );(2)求函數
);(2)求函數 的值域(答:
的值域(答: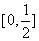 )
)
③ 型,通常用判別式法;如已知函數
型,通常用判別式法;如已知函數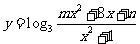 的定義域為R,值域為[0,2],求常數
的定義域為R,值域為[0,2],求常數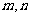 的值(答:
的值(答: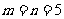 )
)
④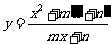 型,可用判別式法或均值不等式法,如求
型,可用判別式法或均值不等式法,如求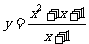 的值域(答:
的值域(答: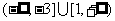 )
)
(7)不等式法--利用基本不等式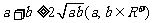 求函數的最值,其題型特征解析式是和式時要求積為定值,解析式是積時要求和為定值,不過有時須要用到拆項、添項和兩邊平方等技巧。如設
求函數的最值,其題型特征解析式是和式時要求積為定值,解析式是積時要求和為定值,不過有時須要用到拆項、添項和兩邊平方等技巧。如設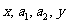 成等差數列,
成等差數列, 成等比數列,則
成等比數列,則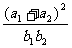 的取值范圍是____________.(答:
的取值范圍是____________.(答: )。
)。
(8)導數法--一般適用于高次多項式函數,如求函數 ,
, 的最小值。(答:-48)
的最小值。(答:-48)
提醒:(1)求函數的定義域、值域時,你按要求寫成集合形式了嗎?(2)函數的最值與值域之間有何關系?
4. 求函數定義域的常用方法(在研究函數問題時要樹立定義域優先的原則):
(1)根據解析式要求如偶次根式的被開方大于零,分母不能為零,對數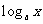 中
中 且
且 ,三角形中
,三角形中 , 最大角
, 最大角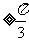 ,最小角
,最小角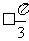 等。如(1)函數
等。如(1)函數 的定義域是____(答:
的定義域是____(答: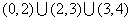 );(2)若函數
);(2)若函數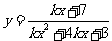 的定義域為R,則
的定義域為R,則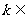 _______(答:
_______(答: );(3)函數
);(3)函數 的定義域是
的定義域是 ,
, ,則函數
,則函數 的定義域是__________(答:
的定義域是__________(答: );(4)設函數
);(4)設函數 ,①若
,①若 的定義域是R,求實數
的定義域是R,求實數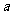 的取值范圍;②若
的取值范圍;②若 的值域是R,求實數
的值域是R,求實數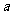 的取值范圍(答:①
的取值范圍(答:① ;②
;②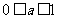 )
)
(2)根據實際問題的要求確定自變量的范圍。
(3)復合函數的定義域:若已知 的定義域為
的定義域為 ,其復合函數
,其復合函數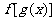 的定義域由不等式
的定義域由不等式 解出即可;若已知
解出即可;若已知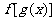 的定義域為
的定義域為 ,求
,求 的定義域,相當于當
的定義域,相當于當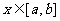 時,求
時,求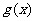 的值域(即
的值域(即 的定義域)。如(1)若函數
的定義域)。如(1)若函數 的定義域為
的定義域為 ,則
,則 的定義域為__________(答:
的定義域為__________(答: );(2)若函數
);(2)若函數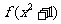 的定義域為
的定義域為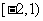 ,則函數
,則函數 的定義域為________(答:[1,5]).
的定義域為________(答:[1,5]).
3. 同一函數的概念。構成函數的三要素是定義域,值域和對應法則。而值域可由定義域和對應法則唯一確定,因此當兩個函數的定義域和對應法則相同時,它們一定為同一函數。如若一系列函數的解析式相同,值域相同,但其定義域不同,則稱這些函數為“天一函數”,那么解析式為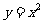 ,值域為{4,1}的“天一函數”共有______個(答:9)
,值域為{4,1}的“天一函數”共有______個(答:9)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com