
4.二面角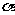 -
-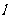 -
- 內一點P,分別作兩個面的垂線PA、PB,A、B為垂足.已知PA=3,PB=2,∠APB=60°求
內一點P,分別作兩個面的垂線PA、PB,A、B為垂足.已知PA=3,PB=2,∠APB=60°求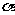 -
-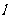 -
- 的大小及P到
的大小及P到 的距離.
的距離.
3. 在棱長為1的正方體ABCD-A1B1C1D1中,E,F分別是AB和AD的中點,則點A1到平面EFB1D1的距離為
在棱長為1的正方體ABCD-A1B1C1D1中,E,F分別是AB和AD的中點,則點A1到平面EFB1D1的距離為
2.異面直線a , b所成的角為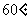 ,過空間一定點P,作直線
,過空間一定點P,作直線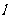 ,使
,使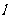 與a ,b 所成的角均為
與a ,b 所成的角均為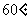 ,這樣的直線
,這樣的直線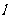 有
條.
有
條.
1.在平面角為600的二面角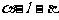 內有一點P,P到α、β的距離分別為PC=2cm,PD=3cm,則P到棱
內有一點P,P到α、β的距離分別為PC=2cm,PD=3cm,則P到棱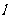 的距離為____________.
的距離為____________.
[例1] 平面 外有兩點A,B,它們與平面
外有兩點A,B,它們與平面 的距離分別為a,b,線段AB上有一點P,且AP:PB=m:n,則點P到平面
的距離分別為a,b,線段AB上有一點P,且AP:PB=m:n,則點P到平面 的距離為_________________.
的距離為_________________.
錯解: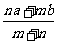 .
.
錯因:只考慮AB在平面同側的情形,忽略AB在平面兩測的情況.
正解: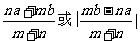 .
.
[例2]與空間四邊形ABCD四個頂點距離相等的平面共有______個.
錯解:4個.
錯因:只分1個點與3個點在平面兩側.沒有考慮2個點與2個點在平面兩側.
正解:7個.
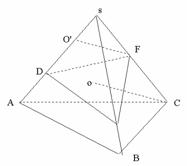
[例3]一個盛滿水的三棱錐形容器,不久發現三條側棱上各有一個小洞D、E、F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用這個容器盛水,則最多可盛原來水的( )
 A.
A.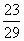 B.
B.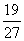 C.
C.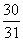 D.
D.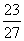
錯解:A、B、C.由過D或E作面ABC的平行面,所截體計算而得.
正解:D.
當平面EFD處于水平位置時,容器盛水最多

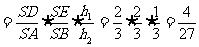
最多可盛原來水得1-
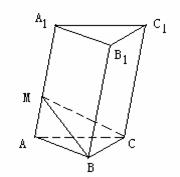
[例4]斜三棱柱ABC-A1B1C1的底面是邊長為a的正三角形,側棱長等于b,一條側棱AA1與底面相鄰兩邊AB、AC都成450角,求這個三棱柱的側面積.
錯解:一是不給出任何證明,直接計算得結果;二是作直截面的方法不當,即“過BC作平面與AA1垂直于M”;三是由條件“∠A1AB=∠A1AC ∠AA1在底面ABC上的射影是∠BAC的平分線”不給出論證.
∠AA1在底面ABC上的射影是∠BAC的平分線”不給出論證.
正解:過點B作BM⊥AA1于M,連結CM,在△ABM和△ACM中,∵AB=AC,∠MAB=∠MAC=450,MA為公共邊,∴△ABM≌△ACM,∴∠AMC=∠AMB=900,∴AA1⊥面BHC,即平面BMC為直截面,又BM=CM=ABsin450=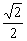 a,∴BMC周長為2x
a,∴BMC周長為2x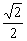 a+a=(1+
a+a=(1+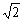 )a,且棱長為b,∴S側=(1+
)a,且棱長為b,∴S側=(1+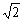 )ab
)ab
[例5]已知CA⊥平面α,垂足為A;AB 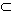 α,BD⊥AB,且BD與α成30°角;AC=BD=b,AB=a.求C,D兩點間的距離.
α,BD⊥AB,且BD與α成30°角;AC=BD=b,AB=a.求C,D兩點間的距離.
解 : 本題應分兩種情況討論:
(1)如下左圖.C,D在α同側:過D作DF⊥α,垂足為F.連BF,則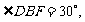 于是
于是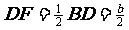 .
.
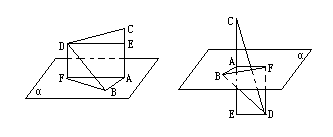 根據三垂線定理BD⊥AB得BF⊥AB.
根據三垂線定理BD⊥AB得BF⊥AB.
在Rt△ABF中,AF=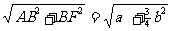
過D作DE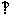 AC于E,則DE=AF,AE=DF=
AC于E,則DE=AF,AE=DF= .所以EC=AC-AE= b-
.所以EC=AC-AE= b-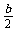 =
=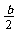 .故
.故
CD=
(2)如上右圖.C,D在α兩側時:同法可求得CD=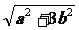
 點 評: 本題是通過把已知量與未知量歸結到一個直角三角形中,應用勾股定理來求解.
點 評: 本題是通過把已知量與未知量歸結到一個直角三角形中,應用勾股定理來求解.
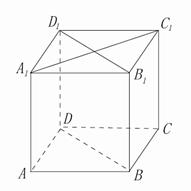
[例6]如圖,在棱長為1的正方體 中,
中,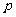 是側棱
是側棱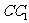 上的一點,
上的一點,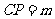 .
.
(1)試確定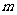 ,使得直線
,使得直線 與平面
與平面 所成角的正切值為
所成角的正切值為 ;
;
(2)在線段 上是否存在一個定點
上是否存在一個定點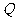 ,使得對任意的
,使得對任意的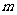 ,
,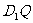 在平面
在平面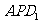 上的射影垂直于
上的射影垂直于 .
.
并證明你的結論.
解:解法一(1)連AC,設AC與BD相交于點O,AP與平面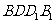 相交于點,,連結OG,因為
相交于點,,連結OG,因為
 PC∥平面
PC∥平面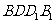 ,平面
,平面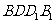 ∩平面APC=OG,
∩平面APC=OG,
故OG∥PC,所以,OG=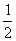 PC=
PC=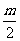 .
.
又AO⊥BD,AO⊥BB1,所以AO⊥平面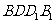 ,
,
故∠AGO是AP與平面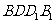 所成的角.
所成的角.
在Rt△AOG中,tan AGO=
AGO=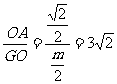 ,即m=
,即m=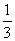 .
.
所以,當m=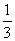 時,直線AP與平面
時,直線AP與平面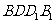 所成的角的正切值為
所成的角的正切值為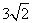 .
.
(2)可以推測,點Q應當是AICI的中點O1,因為
D1O1⊥A1C1, 且 D1O1⊥A1A ,所以 D1O1⊥平面ACC1A1,
又AP 平面ACC1A1,故 D1O1⊥AP.
平面ACC1A1,故 D1O1⊥AP.
那么根據三垂線定理知,D1O1在平面APD1的射影與AP垂直。
 解法二:(1)建立如圖所示的空間直角坐標系,則A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1)
解法二:(1)建立如圖所示的空間直角坐標系,則A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1)
所以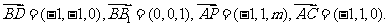
又由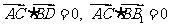 知,
知,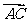 為平面
為平面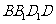 的一個法向量。
的一個法向量。
設AP與平面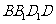 所成的角為
所成的角為 ,則
,則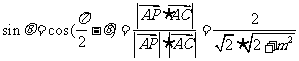 。依題意有
。依題意有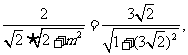 解得
解得 。故當
。故當 時,直線AP與平面
時,直線AP與平面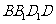 所成的角的正切值為
所成的角的正切值為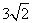 。
。
(2)若在A1C1上存在這樣的點Q,設此點的橫坐標為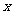 ,則Q(x,1-
,則Q(x,1-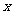 ,1),
,1),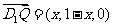 。依題意,對任意的m要使D1Q在平面APD1上的射影垂直于AP,等價于D1Q⊥AP
。依題意,對任意的m要使D1Q在平面APD1上的射影垂直于AP,等價于D1Q⊥AP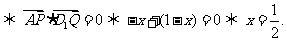 即Q為A1C1的中點時,滿足題設要求。
即Q為A1C1的中點時,滿足題設要求。
[例7]在梯形ABCD中,∠ADC=90°,AB∥DC,AB=1,DC=2,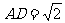 ,P為平面ABCD外一點,PAD是正三角形,且PA⊥AB,
,P為平面ABCD外一點,PAD是正三角形,且PA⊥AB,
求:(1)平面PBC和平面PAD所成二面角的大小;
(2)D點到平面PBC的距離.
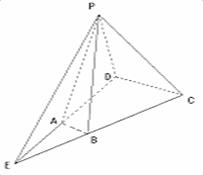 解: (1)設AD∩BC=E,可知PE是平面PBC和平面PAD的交線,依題設條件得PA=AD=AE,則∠EPD=90°,PD⊥PE
解: (1)設AD∩BC=E,可知PE是平面PBC和平面PAD的交線,依題設條件得PA=AD=AE,則∠EPD=90°,PD⊥PE
又PA⊥AB,DA⊥AB,故AB⊥平面PAD.
∵ DC∥AB,∴ DC⊥平面PAD.
由PE⊥PC得PE⊥PD,∠DPC是平面PBC與平面PAD所成二面角的平面角.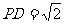 ,DC=2,tan
,DC=2,tan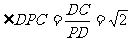 ,
, .
.
(2)由于PE⊥PD,PE⊥PC,故PE⊥平面PDC,
因此平面PDC⊥平面PBC,
作DH⊥PC,H是垂足,則DH是D到平面PBC的距離.
在Rt△PDC中,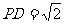 ,DC=2,
,DC=2,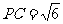 ,
, .
.
平面PBC與平面PAD成二面角的大小為arctan ,D到平面PBC的距離為
,D到平面PBC的距離為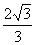 .
.
[例8] 半徑為1的球面上有A、B、C三點,A與B和A與C的 球面距離都是
球面距離都是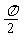 ,B與C的球面距離是
,B與C的球面距離是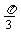 ,求過A、B、C三點的截面到球心O距離.
,求過A、B、C三點的截面到球心O距離.
分析 : 轉化為以球心O為頂點,△ABC為底面的三棱錐問題解決.
由題設知△OBC是邊長為1的正三角形,△AOB和△AOC是腰長為1的全等的等腰三角形.
取BC中點D,連AD、OD,易得BC⊥面AOD,進而得面AOD⊥面ABC,過O作OH⊥AD于H,則OH⊥面ABC,OH的長即為
所求,在Rt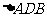 中,AD=
中,AD=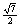 ,故在Rt
,故在Rt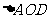 ,OH=
,OH=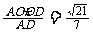
點評: 本題若注意到H是△ABC的外心,可通過解△ABC和△AHO得OH.或利用體積法.
5.要注意距離和角在空間求值中的相互作用,以及在求面積和體積中的作用.
4.球面上兩點間的距離是指經過這兩點的球的大圓的劣弧的長,關鍵在于畫出經過兩點的大圓以及小圓.
3.空間距離的計算一般將其轉化為兩點間的距離.求點到平面距離時,可先找出點在平面內的射影(可用兩個平面垂直的性質),也可用等體積轉換法求之.另外要注意垂直的作用.球心到截面圓心的距離由勾股定理得
2.求二面角大小時,關鍵是找二面角的平面角,可充分利用定義法或垂面法等.
1.求空間角的大小時,一般將其轉化為平面上的角來求,具體地將其轉化為某三角形的一個內角.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com