
5.實質
能量轉化:
4.比較光合作用光反應與暗反應之間的關系
|
|
光反應 |
暗反應 |
|
|
區 別 |
反應條件 |
|
|
|
反應場所 |
|
|
|
|
反應速度 |
|
|
|
|
原料產物 |
原料: 產物: |
原料: 產物: |
|
|
物質變化 |
|
|
|
|
能量變化 |
|
|
|
|
聯系 |
光反應是準備階段,為暗反應提供了 ,暗反應則是光反應的繼續。 |
 物質轉化:
;
物質轉化:
;
3.總反應式:
2.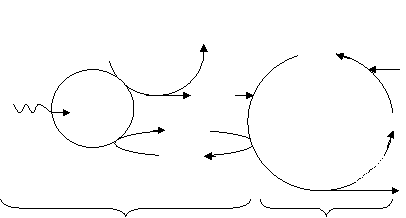 過程
過程
光反應 暗反應
1.概念:綠色植物通過 ,利用 ,把 和 合成為儲存有
的有機物,并且釋放出 的過程。
 分布:
分布:
葉綠素a:呈 色
葉綠素 吸收
葉綠素b:呈 色
分類 胡蘿卜素:呈 色
類胡蘿卜素 吸收
葉綠體 葉黃素: 呈 色
色素
分布:
作用:
酶 :分布于
 1648年海爾蒙特的實驗,證明
1648年海爾蒙特的實驗,證明
1864年薩克斯通過實驗成功地證明
1880年恩吉爾曼用水綿和好氧性細菌設計并完成實驗,
證明了
1930年魯賓和卡門采用同位素標記法研究證明了
1,正反詞語:
下面給出一些關鍵詞的否定:
|
正面 語詞 |
等于 |
大于 |
小于 |
是 |
全 |
都是 |
至少一個 |
至多 一個 |
|
否定 |
不等于 |
不大于 (小于等于) |
不小于 (大于等于) |
不是 |
不全 |
不都是 |
一個也 沒有 |
至少 兩個 |
2,對數函數圖象
|
圖 象 |
 |
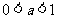 |

|
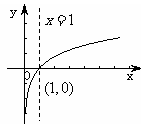


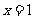


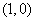 ,即當
,即當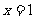 時,
時,
 上是減函數
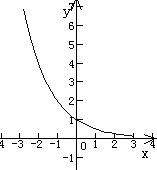
上是減函數3,指數函數圖象
|
|
 |
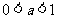 |
|
圖象 |
 |
 |
|
性質 |
(1)定義域: |
|
(2)值域: |
||
(3)過點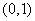 ,即 ,即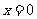 時 時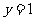 |
||
(4)在 上是增函數 上是增函數 |
(4)在 上是減函數 上是減函數 |
4,同角三角函數的關系圖象
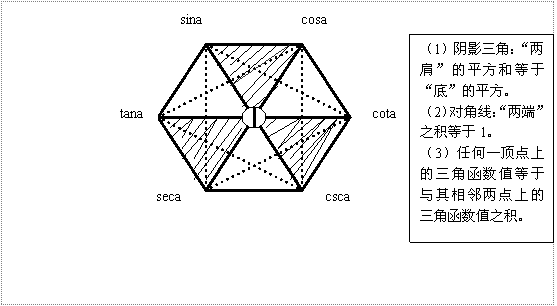

5,正弦、余弦、正切函數圖象
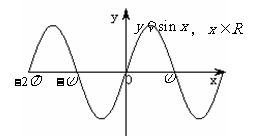

Y=tanx
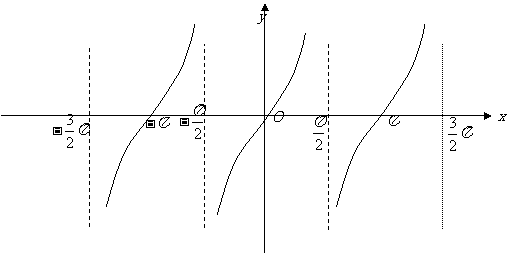
|
函 數 |
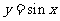 |
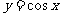 |
Y = tanx |
|
定義域 |
R |
R |
 |
|
值域 |
[-1,1] |
[-1,1] |
R |
|
對稱點 |
 |
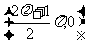 |
 |
|
對稱軸 |
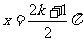 |
 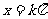 |
無 |
|
增區間 |
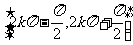 |
 |
 |
|
減區間 |
 |
 |
無 |
|
周期性 |
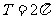 |
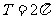 |
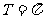 |
|
奇偶性 |
奇函數 |
偶函數 |
奇函數 |
附:反三角函數的主值區間:
|
反三角函數 |
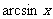 |
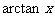 |
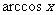 |
|
定義域 |
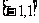 |
R |
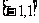 |
|
主值區間(值域) |
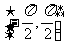 |
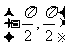 |
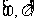 |
8,圓的三種方程:
|
名稱 |
形式 |
圓心 |
半徑 |
條件 |
|
標準方程 |
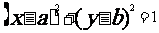 |
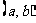 |
r |
r>0 |
|
參數方程 |
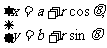 |
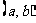 |
r |
r>0 |
|
一般方程 |
 |
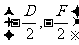 |
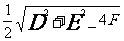 |
 |
(1)點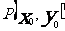 與圓
與圓 的位置關系:
的位置關系:
若 ,則點
,則點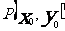 在圓C上;
在圓C上;
若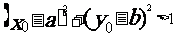 ,則點
,則點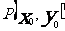 在圓C外;
在圓C外;
若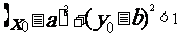 ,則點
,則點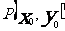 在圓C內;
在圓C內;
(2)直線 與圓
與圓 的位置關系:
的位置關系:
①聯立 
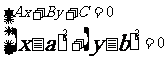 消去不償失得:
消去不償失得:
 ,則
,則 ,直線
,直線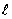 與圓
與圓 的位置關系:
的位置關系:
 相交;
相交;  相切 ;
相切 ;
 相離 。
相離 。
② 圓心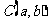 到直線
到直線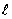 的距離為
的距離為 ,則直線
,則直線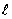 與圓
與圓 的位置關系:
的位置關系:
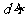 相交;
相交;
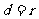 相切 ;
相切 ;
 相離 。
相離 。
(3)圓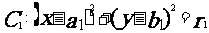 與圓
與圓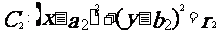 的位置關系:
的位置關系:
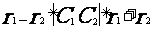 相交;
相交;
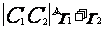 相離;
相離;
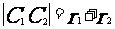 外切;
外切;
 內切。
內切。
(4)半弦長與弦心距的平方和等于半徑的平方。
(5)弦的垂直平分線經過圓心。
(6)圓心到切線的距離等于半徑。
9,橢圓
|
第一定義 |
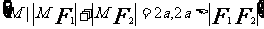 |
|
||
|
第二定義 |
 |
|
||
|
方 程 |
 |
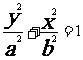 |
|
|
|
圖 象 |
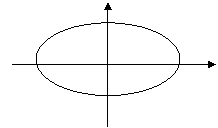  |
  |
|
|
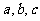 關 系 關 系 |
 |
|
||
|
范 圍 |
 |
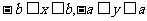 |
|
|
|
頂 點 |
 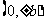 |
 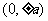 |
|
|
|
對 稱
性 |
關于 軸成軸對稱、關于原點成中心對稱 軸成軸對稱、關于原點成中心對稱 |
|
||
|
離 心
率 |
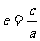 |
|
||
|
焦 點 |
 |
 |
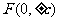 |
|
|
準 線 |
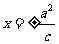 |
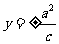 |
|
|
|
焦點三角形面積公式 |
 |
|
||
(1)點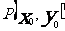 與橢圓C:
與橢圓C: 的位置關系:
的位置關系:
若 ,則點
,則點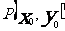 在橢圓C上;
在橢圓C上;
若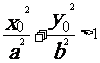 ,則點
,則點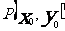 在橢圓C外;
在橢圓C外;
若 ,則點
,則點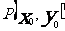 在橢圓C內;
在橢圓C內;
(2)直線 與橢圓C:
與橢圓C: 的位置關系判斷:用
的位置關系判斷:用 法。
法。
10,雙曲線
|
第一定義 |
 |
|
|
第二定義 |
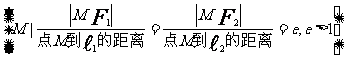 |
|
|
方 程 |
 ( (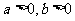 ) ) |
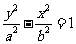 ( (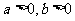 ) ) |
|
圖 象 |
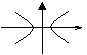 |
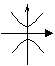 |
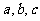 關 系 關 系 |
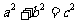 |
|
|
范 圍 |
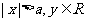 |
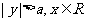 |
|
頂 點 |
 |
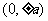 |
|
對 稱 性 |
關于 軸成軸對稱、關于原點成中心對稱 軸成軸對稱、關于原點成中心對稱 |
|
|
漸 近 線 |
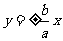 |
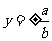 |
|
離 心 率 |
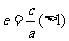 |
|
|
焦 點 |
 |
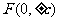 |
|
準 線 |
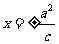 |
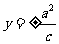 |
|
焦點三角形面積公式 |
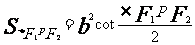 |
11,拋物線
|
定義 |
平面內,到定點F的距離與到定直線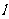 的距離相等的點的軌跡。 的距離相等的點的軌跡。 |
|||
|
方程 |
 |
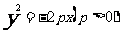 |
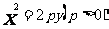 |
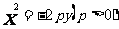 |
|
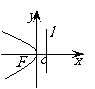
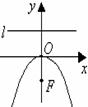
圖
形 |
  |
 |
  |
 |
|
焦點坐標 |
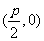 |
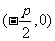 |
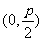 |
 |
|
準線方程 |
 |
 |
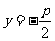 |
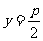 |
|
范圍 |
 |
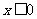 |
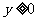 |
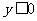 |
|
對稱性 |
 軸 軸 |
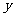 軸 軸 |
||
|
頂點 |
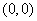 |
|||
|
離心率 |
 |
1,指數運算性質:
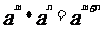 ;
;  ;
; 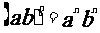 (
(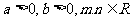 )
)
2,對數運算性質:
 logaM +
logaM + logaN =
logaN = logaMN ;logaM - logaN =
logaMN ;logaM - logaN = loga
loga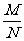 ;alogaN=N ;logaM =
;alogaN=N ;logaM =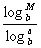 ;
;
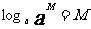 (
(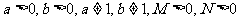 )。
)。
3,等差數列:
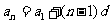 ;
; 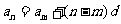 ;
;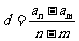
 ;
;
若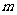 ,
,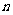 ,
,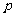 ,
,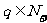 且
且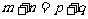 ,則
,則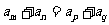 ;
;
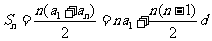 。
。
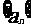 是等差數列
是等差數列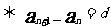 (d為常數)
(d為常數) 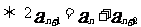
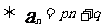 (p,q為常數)
(p,q為常數) (A,B為常數)
(A,B為常數)
4,等比數列:
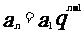 ;
;  (
(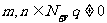 ) ;
) ;
若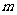 ,
,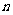 ,
,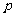 ,
,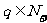 且
且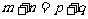 ,則
,則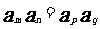
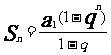 ;
;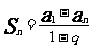 (
( );
);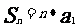 (q=1);
(q=1);
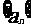 是等比數列
是等比數列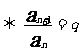 (q為常數)
(q為常數) 
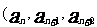 不等于0)
不等于0) 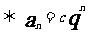 (c,q為非0常數)
(c,q為非0常數)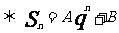 (A,B為常數,A+B=
-1)
(A,B為常數,A+B=
-1)
5, 絕對值不等式定理:
 。
。
6,弧長公式與扇形面積公式: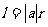
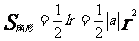 。
。
7,誘導公式:
 與a的三角函數間的關系式即為誘導公式,口訣:“函數名奇變偶不變;符號看象限”。
與a的三角函數間的關系式即為誘導公式,口訣:“函數名奇變偶不變;符號看象限”。
8,同關系角公式:
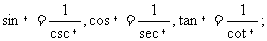
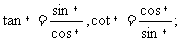
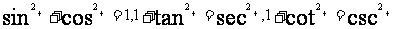
9,和(差)角公式:
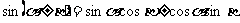 ;
; 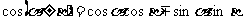 ;
;
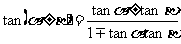 。
。
10,倍角公式:
 ;
;
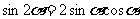 ;
; 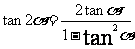 。
。
化簡公式:
 。
。
11,不等式的性質:
(1)三條公理:
(2)五條基本性質:
對稱性: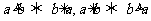
傳遞性: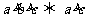
移向法則:
乘法法則:
倒數法則: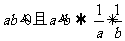
(3)六條基本性質:
加法:
減法:
乘法: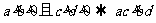
除法: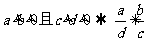
乘方: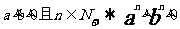
開方: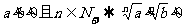
(4)均值不等式:
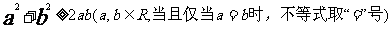



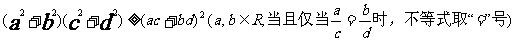
12,不等式的解法:
(1)一元二次不等式的解集與一元二次方程的對應關系:
 |
解集 |
||
|
|
△>0 |
△=0 |
△<0 |
|
ax2+bx+c=0 (a>0) |
x=x1 或x=x2 |
x1=x2=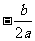 |
無實數根 |
|
ax2+bx+c>0 |
{x|x<x1或x>x2} |
{x|x≠ } } |
R |
|
ax2+bx+c<0 |
{x|x1<x<x2} |
Ø |
ø |
(2)分式不等式:
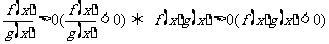 ;
;
 。
。
(3)無理不等式:
 ;
;

(4)指數不等式:
 ;
;
 。
。
(5)對數不等式:
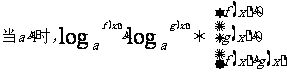
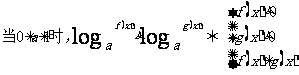
(6)絕對值不等式:
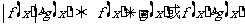 ;
;
 ;
;
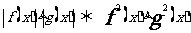
13,正余弦定理:

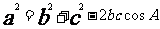
14,三角形面積公式:
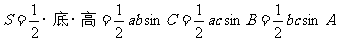
15,平面向量:
 ;
; 
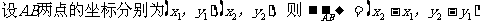
設a= (x1,y1)b= (x2,y2)則: ;
;
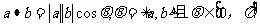 ;a.b= x1 x2 + y1 y2
;a.b= x1 x2 + y1 y2
a∥b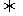 a=
a=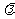 b
b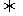 x1 y2 - x2 y1 = 0
x1 y2 - x2 y1 = 0
a⊥b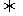 a.b=0
a.b=0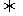 x1 x2 +y1 y2 = 0
x1 x2 +y1 y2 = 0
16,平移公式:
如果點P(x,y)按向量a=(h,k)平移至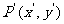 則
則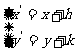
17,定比分點公式:
A(x1,y1),B(x2,y2),點P(x,y)分AB所成的比為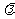 則
則
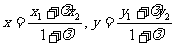
18,距離公式:
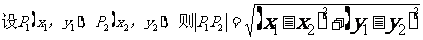
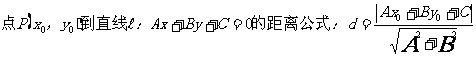
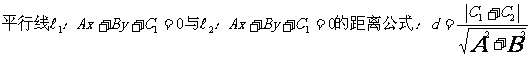 19,斜率公式:
19,斜率公式:
設直線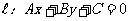 (A≠0)的傾斜角為а(а≠900),方向向量為v=(a,b)(a≠0),直線
(A≠0)的傾斜角為а(а≠900),方向向量為v=(a,b)(a≠0),直線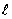 上有兩個點P1(x1,y1)P2(x2,y2)(x1≠x2),則直線
上有兩個點P1(x1,y1)P2(x2,y2)(x1≠x2),則直線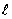 的斜
率
的斜
率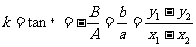 。
。
20,兩直線平行或垂直的充要條件:
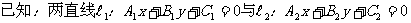
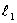 ∥
∥ 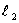
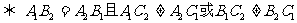
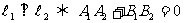 。
。
21,弦長公式:
 22,概率公式:
22,概率公式:
 ;
;
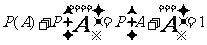 ;
;
 ;
; 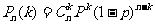
23,平面的基本性質:
公理1: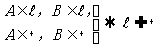
公理2: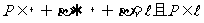
公理3:點A,B,C不公線,則有且只有一個平面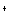 ,使
,使 ,且
,且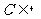 。
。
推論1: 有且只有一個平面
有且只有一個平面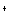 ,使
,使 。
。
推論2: 有且只有一個平面
有且只有一個平面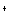 ,使
,使 。
。
推論3: 有且只有一個平面
有且只有一個平面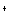 ,使
,使 。:
。:
公理4: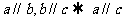 。
。
24,等角定理:
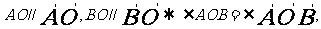 或
或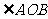 與
與 互補。
互補。
25,直線和平面平行的判定和性質定理:
判定定理:若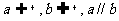 ,則
,則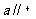 。
。
性質定理:若 ,則
,則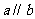 。
。
26,直線和平面垂直的判定和性質定理:
判定定理:若 ,則
,則 。
。
性質定理:若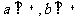 ,則
,則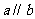 。
。
27,兩個平面平行的判定和性質定理:
判定定理:若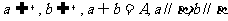 ,則
,則 。
。
性質定理:若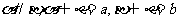 ,則
,則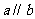 。
。
28,兩個平面垂直的判定和性質定理:
判定定理:直線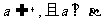 ,則
,則 。
。
性質定理: ,則
,則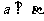 。
。
29,三垂線定理:
 于B,
于B,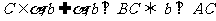 。
。
30,排列數公式:
 。
。
31,組合數的公式和性質:
公式: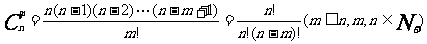
性質1: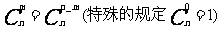
性質2: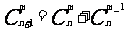 。
。
32,二項式定理:
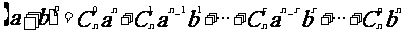
 ;
;
二項式系數的和為: ;
;
二項展開式的通項公式: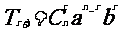
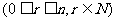 。
。
33,概率與統計:
(1)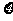 的分布列:
的分布列:
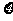 |
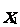 |
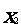 |
。。。 |
 |
。。。 |
|
P |
 |
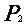 |
。。。 |
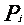 |
。。。 |
(2)二項分布: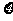 - B(n,p)
- B(n,p)
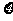 |
0 |
1 |
… |
k |
… |
n |
|
P |
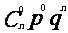 |
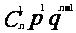 |
… |
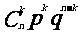 |
… |
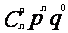 |
(3)期望: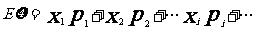
注:①E(a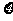 +b)=a.E
+b)=a.E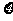 +b ;
+b ;
② 若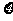 - B(n,p)
, 則E
- B(n,p)
, 則E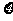 =np .
=np .
(4)標準差: 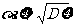
(5)方差: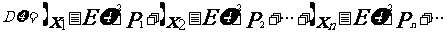
注:①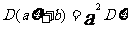 ;
;
② 若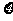 - B(n,p)
, 則D
- B(n,p)
, 則D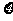 =np(1-p);
=np(1-p);
③
34,無窮等比數列(|q|≤1)的和:
 。
。
35,兩個重要的極限:
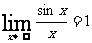 ,
, 。
。
36,函數導數的四則運算法則:
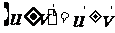 ;
; ;
;
37,導數基本公式:
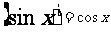 ;
;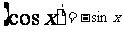 ;
; ;
;
 ;
;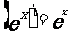 ;
; ;
;
 (C為常數) ;
(C為常數) ; 。
。
38,復數運算法則:
(a+bi)±(c+di)=(a±c)+(b±d)i ; (a+bi)(c+di)=(ac-bd)+(ad+bc)i ;
(a+bi)÷(c+di)= 
 ;
;
39,復數三角形式的運算法則:
 ,
,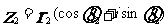 ,
,
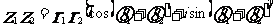 ;
;
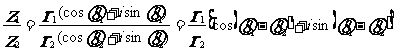 ;
;
乘方: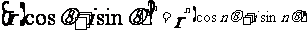
 ;
;
開方: ,其中
,其中

 。
。
4、列方程求解
 ①物體受兩個力: 合成法
①物體受兩個力: 合成法
②物體受多個力: 正交分解法(沿運動方向和垂直于運動方向分解)
 (運動方向)
(運動方向)
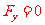 (垂直于運動方向)
(垂直于運動方向)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com