日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

6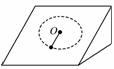．如圖5所示，一輕繩的一端系在固定粗糙斜面上的O點，另一端系一小球，給小球一足夠大的初速度，使小球在斜面上做圓周運動．在此過程中(　)

A．小球的機械能減少

B．重力對小球不做功

C．繩的張力對小球不做功　　　　　　　　　　　　　　　　　　　　 圖5

D．在任何一段時間內，小球克服摩擦力所做的功總是等于小球動能的減少

解析：斜面粗糙，小球受到重力、支持力、摩擦力、繩子拉力，由于除重力做功外，摩擦力做負功，機械能減少，A正確、B錯；繩子張力總是與運動方向垂直，故不做功，C對；小球動能的變化等于合外力做的功，即重力與摩擦力做的功，D錯．

答案：AC

5．(2010·南京模擬)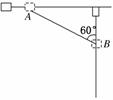有一豎直放置的“T”形架，表面光滑，滑塊A、B分別套在水平桿與豎直桿上，A、B用一不可伸長的輕細繩相連，A、B質量相等，且可看做質點，如圖4所示，開始時細繩水平伸直，A、B靜止．由靜止釋放B后，已知當細繩與豎直方向的夾角為60°時，滑塊B沿著豎直桿下滑的速度為v，則連接A、B的繩長為　　　　　　　　　　　　　 (　)

A.　 　　　　　B.　　　　　 C. 　　　　　　　　D. 　　　　　　圖4

解析：設滑塊A的速度為v_A，因繩不可伸長，兩滑塊沿繩方向的分速度大小相等，得：v_Acos30°＝v_Bcos60°，又v_B＝v，設繩長為l，由A、B組成的系統機械能守恒得：mglcos60°＝mv_A²+mv²，以上兩式聯立可得：l＝，故選D.

答案：D

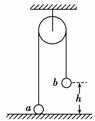
4. (2008·全國卷Ⅱ)如圖3所示，一很長的、不可伸長的柔軟輕繩跨過光滑

定滑輪，繩兩端各系一小球a和b.a球質量為m，靜置于地面；b球質　

量為3m，用手托住，高度為h，此時輕繩剛好拉緊．從靜止開始釋放b　

后，a可能達到的最大高度為　　　　　　　　　　　　　　　 (　)

A．h　　　　　　　　　 　B．1.5h　　　　　　　　　　　　　　　 圖3

C．2h　 　　　　　　　　　　　D．2.5h

解析：在b落地前，a、b組成的系統機械能守恒，且a、b兩物體速度大小相等，根據

機械能守恒定律可知：3mgh－mgh＝(m+3m)v²⇒v＝

b球落地時，a球高度為h，之后a球向上做豎直上拋運動，上升過程中機械能守恒，mv²

＝mgΔh，所以Δh＝＝，即a可能達到的最大高度為1.5h，B項正確．

答案：B

3．(2010·連云港模擬)如圖2所示，在高1.5 m的光滑平臺上有一個質量為2 kg的小球被一細線拴在墻上，球與墻之間有一根被壓縮的輕質彈簧．當燒斷細線時，小球被彈出，小球落地時的速度方向與水平方向成60°角，則彈簧被壓縮時具有的彈性勢能為(g＝10 m/s²)　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　(　)

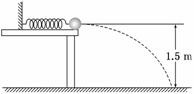
圖2

A．10 J 　　　　　B．15 J　　　　 C．20 J 　　　　　　　　D．25 J

解析：由h＝gt²和v_y＝gt得：v_y＝ m/s，

落地時，tan60°＝可得：

v₀＝＝ m/s，

由機械能守恒得：E_p＝mv₀²，

可求得：E_p＝10 J，故A正確．

答案：A

2.如圖1所示，具有一定初速度的物塊，沿傾角為30°的粗糙斜面向上運動的過程中，受一個恒定的沿斜面向上的拉力F作用，這時物塊的加速度大小為4 m/s²，方向沿斜面向下，那么，在物塊向上運動的過程中，下列說法正確的是　　　　　　　　　　　　　　　　　　　　　　　　　 (　)　　　　 　圖1

A．物塊的機械能一定增加

B．物塊的機械能一定減小

C．物塊的機械能可能不變

D．物塊的機械能可能增加也可能減小

解析：機械能變化的原因是非重力、彈力做功，題中除重力外，有拉力F和摩擦力F_f

做功，則機械能的變化決定于F與F_f做功大小關系．

由mgsinα+F_f－F＝ma知：F－F_f＝mgsin30°－ma＞0，即F＞F_f，故F做正功多于克

服摩擦力做功，故機械能增加．A項正確．

答案：A

1．(2010·常州模擬)質量為m的小球從高H處由靜止開始自由下落，以地面作為參考平面．當小球的動能和重力勢能相等時，重力的瞬時功率為　　　　　　　　　　　　　 (　)

A．2mg　　　　 　B．mg

C.mg　 　　　　　　　　D.mg

解析：動能和重力勢能相等時，下落高度為h＝，速度v＝＝，故P＝mg·v＝mg，B選項正確．

答案：B

12．(14分)(2010·常州模擬)在如圖11所示的裝置中，兩個光滑的定滑輪的半徑很小，表面粗糙的斜面固定在地面上，斜面的傾角為θ＝30°.用一根跨過定滑輪的細繩連接甲、乙兩物體，把甲物體放在斜面上且連線與斜面平行，把乙物體懸在空中，并使懸線拉直且偏離豎直方向α＝60°.現同時釋放甲、乙兩物體，乙物體將在豎直平面內振動，當乙物體運動經過最高點和最低點時，甲物體在斜面上均恰好未滑動．已知乙物體的質量為m＝1 kg，若取重力加速度g＝10 m/s².試求：

圖11

(1)乙物體運動經過最高點和最低點時懸繩的拉力大小；

(2)甲物體的質量及斜面對甲物體的最大靜摩擦力．

解析：(1)設乙物體運動到最高點時，繩子上的彈力為F_T1

對乙物體F_T1＝mgcosα＝5 N

當乙物體運動到最低點時，繩子上的彈力為F_T2

對乙物體由機械能守恒定律：mgl(1－cosα)＝mv²

又由牛頓第二定律：F_T2－mg＝m

得：F_T2＝mg(3－2cosα)＝20 N.

(2)設甲物體的質量為M，所受的最大靜摩擦力為F_f，乙在最高點時甲物體恰好不下滑，有：Mgsinθ＝F_f+F_T1

得：Mgsinθ＝F_f+mgcosα

乙在最低點時甲物體恰好不上滑，有：

Mgsinθ+F_f＝F_T2

得：Mgsinθ+F_f＝mg(3－2cosα)

可解得：M＝＝2.5 kg

F_f＝mg(1－cosα)＝7.5 N.

答案：(1)5 N　20 N　(2)2.5 kg　7.5 N

11．(12分)隨著經濟的持續發展，人民生活水平的不斷提高，近年來我國私家車數量快速增長，高級和一級公路的建設也正加速進行．為了防止在公路彎道部分由于行車速度過大而發生側滑，常將彎道部分設計成外高內低的斜面．如果某品牌汽車的質量為m，汽車行駛時彎道部分的半徑為r，汽車輪胎與路面的動摩擦因數為μ，路面設計的傾角為θ，如圖10所示．(重力加速度g取10 m/s²)

圖10

(1)為使汽車轉彎時不打滑，汽車行駛的最大速度是多少？

(2)若取sinθ＝，r＝60 m，汽車輪胎與雨雪路面的動摩擦因數為μ＝0.3，則彎道部分

汽車行駛的最大速度是多少？

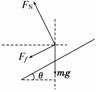解析：(1)受力分析如圖所示，

豎直方向：

F_Ncosθ=mg+F_fsinθ；

水平方向：

F_Nsinθ+F_fcosθ=m ，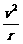

又F_f=μF_N，

可得v= .

(2)代入數據可得：v=14.6 m/s.

答案：(1) 　(2)14.6 m/s

10．(11分)(2008·廣東高考)有一種叫“飛椅”的游樂項目，示意圖如圖9所示，長　

為L的鋼繩一端系著座椅，另一端固定在半徑為r的水平轉盤邊緣，轉盤可繞

穿過其中心的豎直軸轉動．當轉盤以角速度ω勻速轉動時，鋼繩與轉軸在同一

豎直平面內，與　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 圖9

豎直方向的夾角為θ，不計鋼繩的重力，求轉盤轉動的角速度ω與夾角θ的關系．

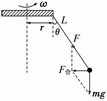解析：設座椅的質量為m，勻速轉動時，座椅的運動半徑為

R=r+Lsinθ　　　　　　　　　　　　　　　　　　　　　　 ①

受力分析如右圖，由牛頓第二定律，有

F_合＝mgtanθ　　　　　　　　　　　　　　　　　　　　　　 ②

F_合＝mω²R　　　　　　　　　　　　　　　　　　　　　　 ③

聯立①②③，得轉盤角速度ω與夾角θ的關系

ω＝ .

答案：ω＝

9．(2010·南通模擬)如圖8所示，小球在豎直放置的光滑圓形管道內做圓周

運動，內側壁半徑為R，小球半徑為r，則下列說法正確的是(　)

A．小球通過最高點時的最小速度v_min＝

B．小球通過最高點時的最小速度v_min＝0　　　　　　　　　　　　　　　　　 圖8

C．小球在水平線ab以下的管道中運動時，內側管壁對小球一定無作用力

D．小球在水平線ab以上的管道中運動時，外側管壁對小球一定有作用力

解析：小球沿管上升到最高點的速度可以為零，故A錯誤，B正確；小球在水平線ab以下的管道中運動時，由外側管壁對小球的作用力F_N與球重力在背離圓心方向的分力F_mg的合力提供向心力，即：F_N－F_mg＝m，因此，外側管壁一定對球有作用力，而內側壁無作用力，C正確；小球在水平線ab以上的管道中運動時，小球受管壁的作用力與小球速度大小有關，D錯誤．

答案：BC