日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

1. 條件探索型--結(jié)論明確，而需探索發(fā)現(xiàn)使結(jié)論成立的條件的題目。

2. 開(kāi)放型問(wèn)題

1. 探索型問(wèn)題

5. 探究存在性型

　　 探究存在性型問(wèn)題是指在一定的條件下，判斷某種數(shù)學(xué)對(duì)象是否存在的問(wèn)題，它有結(jié)論存在和結(jié)論不存在兩種情形，解答這類(lèi)問(wèn)題，一般先對(duì)結(jié)論作肯定存在的假設(shè)，然后由此肯定的假設(shè)出發(fā)，結(jié)合已知條件進(jìn)行推理論證，若導(dǎo)出矛盾，則否定先前假設(shè)；若推出合理的結(jié)論，則說(shuō)明假設(shè)正確，由此得出問(wèn)題的結(jié)論。

　 例16. 已知：點(diǎn)A()在拋物線上

　　 (1)求拋物線的對(duì)稱(chēng)軸；

　　 (2)若點(diǎn)B與點(diǎn)A關(guān)于拋物線的對(duì)稱(chēng)軸對(duì)稱(chēng)，問(wèn)是否存在與拋物線只交于一點(diǎn)B的直線。如果存在，求符合條件的直線；如果不存在，說(shuō)明理由。

　　 分析：要求過(guò)拋物線上點(diǎn)B且僅交拋物線于一點(diǎn)的直線，除了應(yīng)用判別式解出直線外，不要遺漏與對(duì)稱(chēng)軸平行的這一條直線。

　 　解：(1)

　　 <1>假設(shè)存在直線只有一個(gè)交點(diǎn)

　　 <2> 過(guò)B且與拋物線的對(duì)稱(chēng)軸平行的直線是，也與拋物線只有一個(gè)交點(diǎn)

　　 所以符合條件的直線為

　 例17. 已知拋物線，其頂點(diǎn)在x軸的上方，它與y軸交于點(diǎn)C(0，3)與x軸交于點(diǎn)A及點(diǎn)B(6，0)，又知方程兩根的平方和等于40。

　　 (1)求此拋物線的解析式；

　　 (2)試問(wèn)：在此拋物線上是否存在一點(diǎn)P，在x軸上方且使。如果存在，求出點(diǎn)P的坐標(biāo)，如果不存在，說(shuō)明理由。

　　 解：(1)設(shè)是方程的兩根

　　 拋物線頂點(diǎn)在x軸上方，且與y軸交于點(diǎn)C(0，3)，與x軸交于點(diǎn)B(6，0)

　　 (2)假設(shè)拋物線上有一點(diǎn)P(x,y)使

　　 拋物線的頂點(diǎn)坐標(biāo)為(2，4)，y的最大值是4

　　 點(diǎn)P(x，6)不在拋物線上，即不存在點(diǎn)P在x軸上方且使

　 例18. 如圖，已知中，AB=4，點(diǎn)D在AB邊上移動(dòng)(點(diǎn)D不與A、B重合)，DE//BC交AC于E，連結(jié)CD。設(shè)。

　　 (1)當(dāng)D為AB中點(diǎn)時(shí)，求的值；

　　 (2)若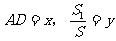，求y關(guān)于x的函數(shù)關(guān)系式及自變量x的取值范圍；

　　 (3)是否存在點(diǎn)D，使得成立？若存在，求出D點(diǎn)位置；若不存在，請(qǐng)說(shuō)明理由。

　　 解：(1)

　　 (3)不存在點(diǎn)D，使得成立。理由：假設(shè)存在點(diǎn)D，使得成立，那么

　　6. 實(shí)驗(yàn)操作型

　　 數(shù)學(xué)不僅是思維科學(xué)，也是實(shí)驗(yàn)科學(xué)，通過(guò)實(shí)驗(yàn)操作，觀察猜想，調(diào)整等合情推理，得到數(shù)學(xué)結(jié)論，近年來(lái)，各地中考試題常以此來(lái)考查學(xué)生的數(shù)學(xué)實(shí)踐能力和創(chuàng)新能力，這種實(shí)驗(yàn)操作形式也是進(jìn)行科學(xué)研究的最基本形式。

　　 例16(北京市西城區(qū)2002年中考題)也是實(shí)驗(yàn)操作性試題，它先通過(guò)學(xué)生動(dòng)手測(cè)量，然后自己再作圖測(cè)量，逐步領(lǐng)悟到一個(gè)猜想，最后對(duì)猜想加以論證。

　 例19. 取一張矩形的紙進(jìn)行折疊，具體操作過(guò)程如下：

　　 第一步：先把矩形ABCD對(duì)折，折痕為MN，如圖1；

　　 第二步：再把B點(diǎn)疊在折痕線MN上，折痕為AE，點(diǎn)B在MN上的對(duì)應(yīng)點(diǎn)為，得，如圖2；

　　 第三步：沿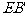線折疊得折痕EF，如圖3。

　　 利用展開(kāi)圖4探究：

　　 (1)是什么三角形？證明你的結(jié)論；

　　 (2)對(duì)于任一矩形，按照上述方法是否都能折出這種三角形？請(qǐng)說(shuō)明理由。

　　 (1)證明：是等邊三角形

　　 證法一：由平行線分線段定理得PE=PA

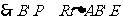　　 斜邊上的中線

　　 證法二：完全重合

　　 (2)不一定

　　 由以上推證可知當(dāng)矩形的長(zhǎng)恰好等于等邊的邊AF時(shí)，即矩形的寬：長(zhǎng)=AB：AF=時(shí)正好能折出。如果設(shè)矩形的長(zhǎng)為a，寬為b，可知

　　 當(dāng)時(shí)，按此法一定能折出等邊三角形；

　　 當(dāng)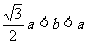時(shí)，按此法無(wú)法折出完整的等邊三角形。

　　 由以上幾例看出，解探索性問(wèn)題實(shí)際是經(jīng)歷一次探索、發(fā)現(xiàn)、猜想、證明的思維過(guò)程，有利于培養(yǎng)和發(fā)展創(chuàng)新意識(shí)和實(shí)踐能力。

4. 探究結(jié)論型

　　 探求結(jié)論型問(wèn)題是指由給定的已知條件探求相應(yīng)的結(jié)論的問(wèn)題。解答這類(lèi)問(wèn)題的思路是：從所給條件(包括圖形特征)出發(fā)，進(jìn)行探索、歸納，大膽猜想出結(jié)論，然后對(duì)猜想的結(jié)論進(jìn)行推理、證明。

　 例13. 如圖，公路上有A、B、C三站，一輛汽車(chē)在上午8時(shí)從離A站10千米的P地出發(fā)向C站勻速前進(jìn)，15分鐘后離A站20千米。

　　 (1)設(shè)出發(fā)x小時(shí)后，汽車(chē)離A站y千米，寫(xiě)出y與x之間的函數(shù)關(guān)系式；

　　 (2)當(dāng)汽車(chē)行駛到離A站150千米的B站時(shí)，接到通知要在中午12點(diǎn)前趕到離B站30千米的C站。汽車(chē)若按原速能否按時(shí)到達(dá)？若能，是在幾點(diǎn)幾分到達(dá)；若不能，車(chē)速最少應(yīng)提高到多少？

　　 分析：這是生活中的一個(gè)實(shí)際問(wèn)題。解第(1)問(wèn)的關(guān)鍵是讀懂題意，求出汽車(chē)從P地出發(fā)向C站勻速前進(jìn)的速度。

　　 第(2)問(wèn)，沒(méi)有給出明確的結(jié)論，需要根據(jù)所給的條件探求，汽車(chē)行駛到B站后，若按原速行駛，到達(dá)C站的時(shí)間。

　　 解：(1)汽車(chē)從P地出發(fā)向C站勻速前進(jìn)，速度為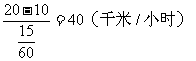

　　 (2)把代入上式，得

　　 汽車(chē)要在中午12點(diǎn)前趕到離B站30千米的C站，車(chē)速最少應(yīng)提高到60千米/時(shí)。

　 例14. 如圖，AB為半圓的直徑，O為圓心，AB=6，延長(zhǎng)BA到F，使FA=AB。若P為線段AF上一個(gè)動(dòng)點(diǎn)(P點(diǎn)與A點(diǎn)不重合)，過(guò)P作半圓的切線，切點(diǎn)為C，作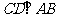，垂足為D。過(guò)B點(diǎn)作，交PC的延長(zhǎng)線于點(diǎn)E，連結(jié)AC、DE。

　　 (1)判斷線段AC、DE所在直線是否平行，并證明你的結(jié)論；

　　 (2)設(shè)AC為x，AC+BE為y，求y與x的函數(shù)關(guān)系式，并寫(xiě)出自變量x的取值范圍。

　　 分析：本題是要根據(jù)圖形的條件探求AC、DE所在直線的位置關(guān)系。本題的難點(diǎn)在于P是一個(gè)動(dòng)點(diǎn)，那么AC與DE也始終在隨P點(diǎn)的運(yùn)動(dòng)而變化。在這種變化中，它們的相對(duì)位置是否有一種特定的聯(lián)系？這就要求我們透過(guò)現(xiàn)象，抓住問(wèn)題的本質(zhì)，考察其中的必然聯(lián)系。可由動(dòng)到靜，把動(dòng)點(diǎn)P設(shè)在AF上的任意一個(gè)位置，根據(jù)題意畫(huà)出草圖，再觀察、猜想、推理、判斷AC與DE是否平行。

　　 解：(1)依題意畫(huà)出圖形，如圖，判斷線段AC、DE所在直線互相平行，即AC//DE。

　　 證明：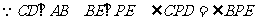

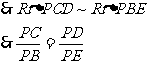
　　 PC與⊙O相切于C點(diǎn)，PAB為⊙O的割線

　　 (2)連結(jié)BC

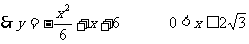
　 例15. 已知：AB為⊙O的直徑，P為AB延長(zhǎng)線上的一個(gè)動(dòng)點(diǎn)，過(guò)點(diǎn)P作⊙O的切線，設(shè)切點(diǎn)為C。

　　 (1)當(dāng)點(diǎn)P在AB延長(zhǎng)線上的位置如圖1所示時(shí)，連結(jié)AC，作APC的平分線，交AC于點(diǎn)D，請(qǐng)你測(cè)量出CDP的度數(shù)；

圖1

(2)當(dāng)點(diǎn)P在AB延長(zhǎng)線上的位置如圖2和圖3所示時(shí)，連結(jié)AC，請(qǐng)你分別在這兩個(gè)圖中用尺規(guī)作APC的平分線(不寫(xiě)作法，保留作圖痕跡)，設(shè)此角平分線交AC于點(diǎn)D，然后在這兩個(gè)圖中分別測(cè)量出CDP的度數(shù)；

　　 猜想：CDP的度數(shù)是否隨點(diǎn)P在AB延長(zhǎng)線上的位置的變化而變化？請(qǐng)對(duì)你的猜想加以證明。

　　 解：(1)測(cè)量結(jié)果：CDP=45^o 　　 (2)(作圖略)

　　 圖2中的測(cè)量結(jié)果：CDP=45^o 　　 圖3中的測(cè)量結(jié)果：CDP=45^o

　　 猜想：CDP=45^o為確定的值，CDP的度數(shù)不隨點(diǎn)P在AB延長(zhǎng)線上的位置的變化而變化。

　　 證法一：連結(jié)BC(如圖)

　　 AB是⊙O的直徑

　　 ⊙O于點(diǎn)C

　　 證法二：連結(jié)OC(如圖)

　　 ⊙O于點(diǎn)C

3. 探究條件型

　　 探究條件型問(wèn)題是指問(wèn)題中結(jié)論明確，而需要完備使結(jié)論成立的條件的題目。解答探求條件型問(wèn)題的思路是，從所給結(jié)論出發(fā)，設(shè)想出合乎要求的一些條件，逐一列出，并進(jìn)行邏輯證明，從而尋找出滿(mǎn)足結(jié)論的條件。

　 例10. 已知：如圖，在中，，垂足為D，E、F分別是AB、AC的中點(diǎn)。

　　 (1)EF和AD之間有什么特殊的位置關(guān)系？請(qǐng)證明你找到的結(jié)論。

　　 (2)要使四邊形AEDF是菱形，需滿(mǎn)足什么條件？

　　 解：(1)EF垂直平分AD

　　 (2)由(1)知

　　 要使四邊形AEDF是菱形，只需要

　　 顯然需要滿(mǎn)足，即滿(mǎn)足是等腰三角形這個(gè)條件。

　 例11. 如圖，已知點(diǎn)A(0，6)、B(3，0)、C(2，0)、M(0，m)，其中m<6，以M為圓心，MC為半徑作圓，則

　　 (1)當(dāng)m為何值時(shí)，⊙M與直線AB相切？

　　 (2)當(dāng)m=0時(shí)，⊙M與直線AB有怎樣的位置關(guān)系？當(dāng)m=3時(shí)，⊙M與直線AB有怎樣的位置關(guān)系？

　　 (3)由(2)驗(yàn)證的結(jié)果，你是否得到啟發(fā)，從而說(shuō)出m在什么范圍內(nèi)取值時(shí)，⊙M與直線AB相離？相交？

　　 ((2)、(3)只寫(xiě)結(jié)果，不必寫(xiě)過(guò)程)

　　 分析：(1)屬探求條件型問(wèn)題，是由給定的結(jié)論--以M為圓心，MC長(zhǎng)為半徑的⊙M與直線AB相切，反溯探究M點(diǎn)的縱坐標(biāo)應(yīng)具備的條件。過(guò)點(diǎn)M作，垂足為H，若MH等于半徑MC，根據(jù)直線與圓相切的判定定理，則⊙M與直線AB相切，再進(jìn)一步追溯使MH=MC時(shí)，M點(diǎn)縱坐標(biāo)m的值。

　　 解：(1)過(guò)點(diǎn)M作，垂足為H，若MH=MC，則以M為圓心、MC長(zhǎng)為半徑的⊙M與AB相切。

　　 ⊙M與直線AB相切

　　 (2)當(dāng)m=0時(shí)，⊙M與直線AB相離；當(dāng)m=3時(shí)，⊙M與直線AB相交

　　 (3)當(dāng)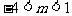時(shí)，⊙M與直線AB相離；當(dāng)或時(shí)，⊙M與直線AB相交。

　 例12. 當(dāng)a取什么數(shù)值時(shí)，關(guān)于未知數(shù)x的方程只有正實(shí)數(shù)根？

　　 分析：本題是探究條件的題目，需要從關(guān)于x的方程只有正實(shí)數(shù)根出發(fā)，考慮a可取的所有值。首先要驗(yàn)證a=0時(shí)，方程為一元一次方程，方程是否有正實(shí)根；然后再考慮，方程為一元二次方程的情況。

　　 解：(1)當(dāng)a=0時(shí)，方程為

　　 (2)當(dāng)

　　 設(shè)方程的兩個(gè)實(shí)數(shù)根為

　　 要使方程只有正實(shí)數(shù)根，由根與系數(shù)的關(guān)系，需

　　 解之，得a<0　　 <2>

　　 由<1>、<2>可得，當(dāng)時(shí)，原方程有兩個(gè)正實(shí)根

綜上討論可知：當(dāng)時(shí)，方程只有正實(shí)數(shù)根

8. 如圖，△ABC中，∠ACB＝90°，AC＝BC，點(diǎn)E在BC上，過(guò)點(diǎn)C作CF⊥AE，垂足為點(diǎn)F，過(guò)點(diǎn)B作BD⊥BC交CF的延長(zhǎng)線于點(diǎn)D，請(qǐng)你仔細(xì)觀察后，在這個(gè)圖形中除了AC＝BC外，再找出一組相等的線段，并說(shuō)明你的理由。

7. 已知：如圖，在中，AB＝AC，∠A＝90°，點(diǎn)D為BC上任一點(diǎn)，DF⊥AB于F，DE⊥AC于E，M為BC的中點(diǎn)。試判斷△MEF是什么形狀三角形，并證明你的猜想。