日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

3. 一個物塊與豎直墻壁接觸，受到水平推力F的作用。力F隨時間變化的規律為(常量k>0)。設物塊從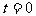時刻起由靜止開始沿墻壁豎直向下滑動，物塊與墻壁間的動摩擦因數為，得到物塊與豎直墻壁間的摩擦力f隨時間t變化的圖象，如圖3所示，從圖線可以得出(　　 )

　　 A. 在時間內，物塊在豎直方向做勻速直線運動

　　 B. 在時間內，物塊在豎直方向做加速度逐漸減小的加速運動

　　 C. 物塊的重力等于a

　　 D. 物塊受到的最大靜摩擦力總等于b

2. 如圖2所示，固定在水平面上的光滑半球，球心O的正上方固定一個小定滑輪，細繩一端拴一小球，小球置于半球面上的A點，另一端繞過定滑輪，如圖所示。今緩慢拉繩使小球從A點滑到半球頂點，則此過程中，小球對半球的壓力大小N及細繩的拉力T大小的變化情況是(　　 )

　　 A. N變大，T變大　　　　　　　　　　 B. N變小，T變大

　　 C. N不變，T變小　　　　　　　　　　 D. N變大，T變小

1. 如圖1所示，在原來靜止的木箱內，放有A物體，A被一伸長的彈簧拉住且恰好靜止，現突然發現A被彈簧拉動，則木箱的運動情況可能是(　　 )

　　 A. 加速下降　　　　　　　　　　　 B. 減速上升

　　 C. 勻速向右運動　　　　　　　　 D. 加速向左運動

5. 處理臨界問題和極值問題的常用方法

　　 涉及臨界狀態的問題叫臨界問題。臨界狀態常指某種物理現象由量變到質變過渡到另一種物理現象的連接狀態，常伴有極值問題出現。如：相互擠壓的物體脫離的臨界條件是壓力減為零；存在摩擦的物體產生相對滑動的臨界條件是靜摩擦力取最大靜摩擦力，彈簧上的彈力由斥力變為拉力的臨界條件為彈力為零等。

　　 臨界問題常伴有特征字眼出現，如“恰好”、“剛剛”等，找準臨界條件與極值條件，是解決臨界問題與極值問題的關鍵。

　 例1. 如圖1所示，一細線的一端固定于傾角為45°的光滑楔形滑塊A的頂端P處，細線另一端拴一質量為m的小球。當滑塊以2g加速度向左運動時，線中拉力T等于多少？

　　 解析：當小球和斜面接觸，但兩者之間無壓力時，設滑塊的加速度為a'

　　 此時小球受力如圖2，由水平和豎直方向狀態可列方程分別為：

　　 解得：

　　 由滑塊A的加速度，所以小球將飄離滑塊A，其受力如圖3所示，設線和豎直方向成角，由小球水平豎直方向狀態可列方程

　　 解得：

　 例2. 如圖4甲、乙所示，圖中細線均不可伸長，物體均處于平衡狀態。如果突然把兩水平細線剪斷，求剪斷瞬間小球A、B的加速度各是多少？(角已知)

　 　解析：水平細線剪斷瞬間拉力突變為零，圖甲中OA繩拉力由T突變為T'，但是圖乙中OB彈簧要發生形變需要一定時間，彈力不能突變。

　　 (1)對A球受力分析，如圖5(a)，剪斷水平細線后，球A將做圓周運動，剪斷瞬間，小球的加速度方向沿圓周的切線方向。

　　 (2)水平細線剪斷瞬間，B球受重力G和彈簧彈力不變，如圖5(b)所示，則

　　 小結：(1)牛頓第二定律是力的瞬時作用規律，加速度和力同時產生、同時變化、同時消失。分析物體在某一時刻的瞬時加速度，關鍵是分析該瞬時前后的受力情況及其變化。

　　 (2)明確兩種基本模型的特點：

　　 A. 輕繩的形變可瞬時產生或恢復，故繩的彈力可以瞬時突變。

　　 B. 輕彈簧(或橡皮繩)在兩端均聯有物體時，形變恢復需較長時間，其彈力的大小與方向均不能突變。

　 例3. 傳送帶與水平面夾角37°，皮帶以10m/s的速率運動，皮帶輪沿順時針方向轉動，如圖6所示。今在傳送帶上端A處無初速地放上一個質量為的小物塊，它與傳送帶間的動摩擦因數為0.5，若傳送帶A到B的長度為16m，g取，則物體從A運動到B的時間為多少？

　 　解析：由于，物體一定沿傳送帶對地下移，且不會與傳送帶相對靜止。

　　 設從物塊剛放上到皮帶速度達10m/s，物體位移為，加速度，時間，因物速小于皮帶速率，根據牛頓第二定律，，方向沿斜面向下。皮帶長度。

　　 設從物塊速率為到B端所用時間為，加速度，位移，物塊速度大于皮帶速度，物塊受滑動摩擦力沿斜面向上，有：

　　 即(舍去)

　　 所用總時間

　 例4. 如圖7，質量的小車停放在光滑水平面上，在小車右端施加一水平恒力F=8N。當小車向右運動速度達到3m/s時，在小車的右端輕放一質量m=2kg的小物塊，物塊與小車間的動摩擦因數，假定小車足夠長，問：

　　 (1)經過多長時間物塊停止與小車間的相對運動？

　　 (2)小物塊從放在車上開始經過所通過的位移是多少？(g取)

　 　解析：(1)依據題意，物塊在小車上停止運動時，物塊與小車保持相對靜止，應具有共同的速度。設物塊在小車上相對運動時間為t，物塊、小車受力分析如圖8：

　　 物塊放上小車后做初速度為零加速度為的勻加速直線運動，小車做加速度為勻加速運動。

　　 由牛頓運動定律：

　　 物塊放上小車后加速度：

　　 小車加速度：

　　 由得：

　　 (2)物塊在前2s內做加速度為的勻加速運動，后1s同小車一起做加速度為的勻加速運動。

　　 以系統為研究對象：

　　 根據牛頓運動定律，由得：

　　 物塊位移

　 例5. 將金屬塊m用壓縮的輕彈簧卡在一個矩形的箱中，如圖9所示，在箱的上頂板和下底板裝有壓力傳感器，箱可以沿豎直軌道運動。當箱以的加速度豎直向上做勻減速運動時，上頂板的傳感器顯示的壓力為6.0 N，下底板的傳感器顯示的壓力為10.0 N。(取)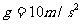

　　 (1)若上頂板傳感器的示數是下底板傳感器的示數的一半，試判斷箱的運動情況。

　　 (2)若上頂板傳感器的示數為零，箱沿豎直方向運動的情況可能是怎樣的？

　　 啟迪：題中上下傳感器的讀數，實際上是告訴我們頂板和彈簧對m的作用力的大小。對m受力分析求出合外力，即可求出m的加速度，并進一步確定物體的運動情況，但必須先由題意求出m的值。

　　 解析：當減速上升時，m受力情況如圖10所示：

　　 (1)

　　 故箱體將作勻速運動或保持靜止狀態。

　　 (2)若，則

　　 即箱體將向上勻加速或向下勻減速運動，且加速度大小大于、等于。

　 例6. 測定病人的血沉有助于對病情的判斷。血液由紅血球和血漿組成，將血液放在豎直的玻璃管內，紅血球會勻速下沉，其下沉的速度稱為血沉，某人血沉為v，若把紅血球看成半徑為R的小球，它在血漿中下沉時所受阻力，為常數，則紅血球半徑R＝___________。(設血漿密度為，紅血球密度為)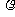

　　 解析：紅血球受到重力、阻力、浮力三個力作用處于平衡狀態，由于這三個力位于同一豎直線上，故可得

　　 即

　　 得：

4. 求解共點力作用下物體的平衡問題常用的方法

　　 (1)有不少三力平衡問題，既可從平衡的觀點(根據平衡條件建立方程求解)--平衡法，也可從力的分解的觀點求解--分解法。兩種方法可視具體問題靈活運用。

　　 (2)相似三角形法：通過力三角形與幾何三角形相似求未知力。對解斜三角形的情況更顯優勢。

　　 (3)力三角形圖解法，當物體所受的力變化時，通過對幾個特殊狀態畫出力圖(在同一圖上)對比分析，使動態問題靜態化，抽象問題形象化，問題將變得易于分析處理。

3. 解決共點力作用下物體的平衡問題思路

　　 (1)確定研究對象：若是相連接的幾個物體處于平衡狀態，要注意“整體法”和“隔離法”的綜合運用；

　　 (2)對研究對象受力分析，畫好受力圖；

　　 (3)恰當建立正交坐標系，把不在坐標軸上的力分解到坐標軸上。建立正交坐標系的原則是讓盡可能多的力落在坐標軸上。

　　 (4)列平衡方程，求解未知量。

2. 應用牛頓第二定律解題的一般步驟

　　 ①確定研究對象；

　　 ②分析研究對象的受力情況畫出受力分析圖并找出加速度方向；

　　 ③建立直角坐標系，使盡可能多的力或加速度落在坐標軸上，并將其余分解到兩坐標軸上；

　　 ④分別沿x軸方向和y軸方向應用牛頓第二定律列出方程；

　　 ⑤統一單位，計算數值。

1. 作用力與反作用力的二力平衡的區別

　　 兩個物體之間的作用力和反作用力總是大小相等，方向相反，作用在一條直線上，公式可寫為。

3. 平衡條件的推論

　　 (1)物體在多個共點力作用下處于平衡狀態，則其中的一個力與余下的力的合力等大反向；

　　 (2)物體在同一平面內的三個不平行的力作用下，處于平衡狀態，這三個力必為共點力；

　　 (3)物體在三個共點力作用下處于平衡狀態時，圖示這三個力的有向線段必構成閉合三角形。