
19.(2009全國卷Ⅱ文)已知等差數(shù)列{ }中,
}中,
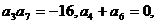 求{
求{ }前n項和
}前n項和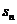 .
. 

解析:本題考查等差數(shù)列的基本性質(zhì)及求和公式運用能力,利用方程的思想可求解。
解:設 的公差為
的公差為 ,則
,則 

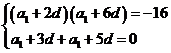
即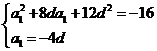
解得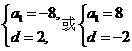
因此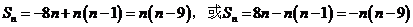
18.(2009山東卷文)等比數(shù)列{ }的前n項和為
}的前n項和為 ,
已知對任意的
,
已知對任意的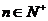 ,點
,點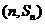 ,均在函數(shù)
,均在函數(shù)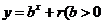 且
且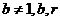 均為常數(shù))的圖像上.
均為常數(shù))的圖像上. 

(1)求r的值;
(11)當b=2時,記 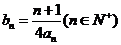 求數(shù)列
求數(shù)列 的前
的前 項和
項和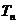
解:因為對任意的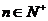 ,點
,點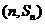 ,均在函數(shù)
,均在函數(shù)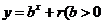 且
且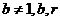 均為常數(shù))的圖像上.所以得
均為常數(shù))的圖像上.所以得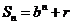 ,
,
當 時,
時,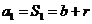 ,
, 

當 時,
時,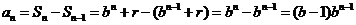 ,
,
又因為{ }為等比數(shù)列, 所以
}為等比數(shù)列, 所以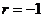 , 公比為
, 公比為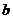 , 所以
, 所以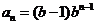
(2)當b=2時,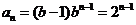 ,
, 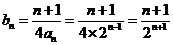
則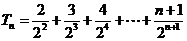
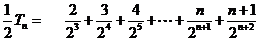


相減,得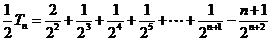
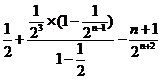
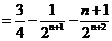
所以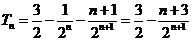
[命題立意]:本題主要考查了等比數(shù)列的定義,通項公式,以及已知 求
求 的基本題型,并運用錯位相減法求出一等比數(shù)列與一等差數(shù)列對應項乘積所得新數(shù)列的前
的基本題型,并運用錯位相減法求出一等比數(shù)列與一等差數(shù)列對應項乘積所得新數(shù)列的前 項和
項和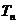 .
.
17.(2009北京文)設數(shù)列 的通項公式為
的通項公式為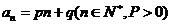 . 數(shù)列
. 數(shù)列 定義如下:對于正整數(shù)m,
定義如下:對于正整數(shù)m,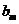 是使得不等式
是使得不等式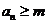 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若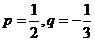 ,求
,求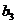 ;
;
(Ⅱ)若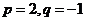 ,求數(shù)列
,求數(shù)列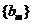 的前2m項和公式;
的前2m項和公式;
(Ⅲ)是否存在p和q,使得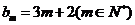 ?如果存在,求p和q的取值范圍;如果不存在,請說明理由.
?如果存在,求p和q的取值范圍;如果不存在,請說明理由.
[解析]本題主要考查數(shù)列的概念、數(shù)列的基本性質(zhì),考查運算能力、推理論證能力、
分類討論等數(shù)學思想方法.本題是數(shù)列與不等式綜合的較難層次題.
解(Ⅰ)由題意,得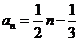 ,解
,解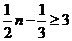 ,得
,得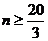 .
. 

∴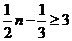 成立的所有n中的最小整數(shù)為7,即
成立的所有n中的最小整數(shù)為7,即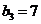 .
.
(Ⅱ)由題意,得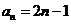 ,
,
對于正整數(shù),由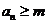 ,得
,得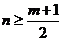 .
.
根據(jù)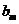 的定義可知
的定義可知
當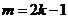 時,
時,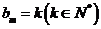 ;當
;當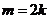 時,
時,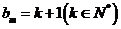 .
.
∴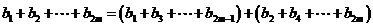
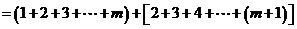
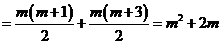 .
.
(Ⅲ)假設存在p和q滿足條件,由不等式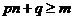 及
及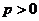 得
得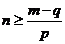 .
.
∵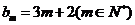 ,根據(jù)
,根據(jù)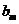 的定義可知,對于任意的正整數(shù)m 都有
的定義可知,對于任意的正整數(shù)m 都有
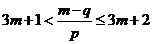 ,即
,即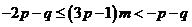 對任意的正整數(shù)m都成立.
對任意的正整數(shù)m都成立.
當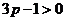 (或
(或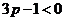 )時,得
)時,得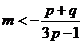 (或
(或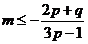 ),
),
這與上述結(jié)論矛盾!
當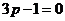 ,即
,即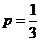 時,得
時,得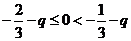 ,解得
,解得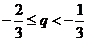 .
.
∴ 存在p和q,使得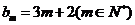 ;
;
p和q的取值范圍分別是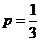 ,
,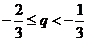 ..
..
16.(2009浙江文)設 為數(shù)列
為數(shù)列 的前
的前 項和,
項和,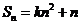 ,
,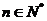 ,其中
,其中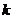 是常數(shù).
是常數(shù).
(I) 求 及
及 ;
;
(II)若對于任意的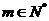 ,
,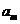 ,
,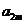 ,
,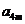 成等比數(shù)列,求
成等比數(shù)列,求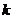 的值.
的值.
解(Ⅰ)當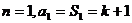 ,
,
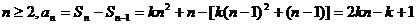 (
(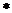 )
)
經(jīng)驗,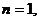 (
(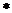 )式成立,
)式成立,
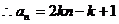
(Ⅱ)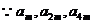 成等比數(shù)列,
成等比數(shù)列,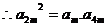 ,
,
即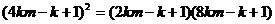 ,整理得:
,整理得: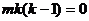 ,
,
對任意的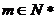 成立,
成立,
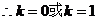
15.(2009遼寧卷理)等差數(shù)列 的前
的前 項和為
項和為 ,且
,且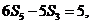 則
則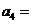
解析 ∵Sn=na1+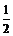 n(n-1)d
n(n-1)d 

∴S5=5a1+10d,S3=3a1+3d
∴6S5-5S3=30a1+60d-(15a1+15d)=15a1+45d=15(a1+3d)=15a4
答案 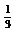
三、解答題
14.(2009全國卷Ⅱ理)設等差數(shù)列 的前
的前 項和為
項和為 ,若
,若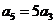 則
則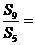
解析 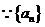 為等差數(shù)列,
為等差數(shù)列,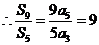
答案 9
13.(2009全國卷Ⅱ文)設等比數(shù)列{ }的前n項和為
}的前n項和為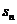 。若
。若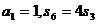 ,則
,則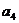 =
×
=
×
答案:3
解析:本題考查等比數(shù)列的性質(zhì)及求和運算,由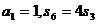 得q3=3故a4=a1q3=3
得q3=3故a4=a1q3=3
12.(2009北京文)若數(shù)列 滿足:
滿足: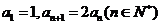 ,則
,則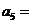 ;前8項的和
;前8項的和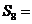 .(用數(shù)字作答)
.(用數(shù)字作答)
答案 225
.解析 本題主要考查簡單的遞推數(shù)列以及數(shù)列的求和問題. 屬于基礎知識、基本運算的考查.
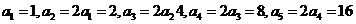 ,
,
易知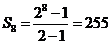 ,∴應填255.
,∴應填255.
11.(2009浙江理)設等比數(shù)列 的公比
的公比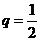 ,前
,前 項和為
項和為 ,則
,則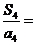 .
.
答案:15
解析 對于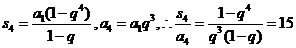
10.(2009全國卷Ⅰ理) 設等差數(shù)列 的前
的前 項和為
項和為 ,若
,若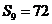 ,則
,則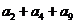 =
=
答案 24
解析 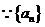 是等差數(shù)列,由
是等差數(shù)列,由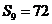 ,得
,得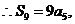
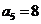

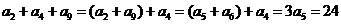 .
. 

湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com