
7.已知函數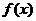 是定義在R上的奇函數,其最小正周期為3,
且
是定義在R上的奇函數,其最小正周期為3,
且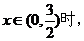


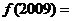
A.4
B.2
C. -2
D.
6.平面 與平面
與平面 外有一條直線
外有一條直線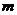 ,如果
,如果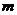 在
在 與
與 內的射影分別是直線
內的射影分別是直線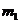 和直線
和直線
 ,給出下列四個命題:
,給出下列四個命題:
①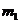 ∥
∥

 ∥
∥ ; ②
; ② ∥
∥

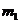 ∥
∥ ;
;
③ ⊥
⊥

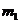 ⊥
⊥ ; ④
; ④ 與
與 相交
相交
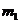 與
與 相交;
相交;
其中正確的命題個數是
A.1 B.2 C.3 D.4
5.設變量 滿足約束條件
滿足約束條件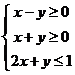 ,則
,則 的最大值為
的最大值為
A. 2 B. 4 C. 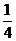 D.
D. 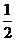
4.記等差數列 的前
的前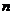 項和為
項和為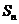 ,若
,若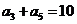 ,
, ,則直線
,則直線
的斜率為
A.-2 B. C.-
C.- D.
D.
3.已知 ,則
,則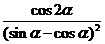 =
=
A. B.
B. C.
C. D.
D.
2.設集合 ,B=
,B=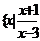 ≤0
≤0 ,那么“
,那么“ ”是“
”是“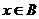 ”的
”的
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既非充分又非必要條件
1.復數 的虛部為
的虛部為
A.1 B.4 C.-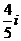 D.-
D.-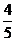
16(本題滿分12分).
在銳角△ 中,內角A、B、C的對邊分別為
中,內角A、B、C的對邊分別為 、
、 、
、 ,且
,且
(Ⅰ)求A的值;
(Ⅱ)求 的取值范圍。
的取值范圍。
17(本題滿分12分).設進入健身中心的每一位健身者選擇甲種健身項目的概率是 ,選擇乙種健身項目的概率是
,選擇乙種健身項目的概率是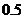 ,且選擇甲種與選擇乙種健身項目相互獨立,各位健身者之間選擇健身項目是相互獨立的。
,且選擇甲種與選擇乙種健身項目相互獨立,各位健身者之間選擇健身項目是相互獨立的。
(Ⅰ)求進入該健身中心的1位健身者選擇甲、乙兩種項目中的一項的概率;
(Ⅱ)求進入該健身中心的4位健身者中,至少有2位既未選擇甲種又未選擇乙種健身項目的概率。
 18(本題滿分12分).
四棱錐
18(本題滿分12分).
四棱錐 中,
中,

 ,
, 平面ABCD,
平面ABCD,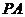 =
=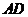 =
= =2,
=2,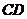 =4。
=4。
(Ⅰ)求證:平面
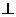 平面
平面 ;
;
(Ⅱ)求點 到平面
到平面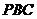 的距離;
的距離;
|
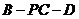 的大小。
的大小。
19(本題滿分13分).
數列 的前
的前 項和為
項和為 ,點
,點 在曲線
在曲線 上。
上。
(Ⅰ)求數列 的通項公式;
的通項公式;
(Ⅱ)設 ,數列
,數列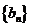 的前
的前 項和為
項和為 ,若
,若 對
對 恒成立,求最大正整數
恒成立,求最大正整數 的值。
的值。
20(本題滿分13分).已知點 (4,0),直線
(4,0),直線 ,和動點
,和動點 。作
。作 ,垂足為
,垂足為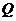 ,且向量
,且向量 ,設點
,設點 的軌跡曲線為
的軌跡曲線為 。
。
(Ⅰ)求曲線 的方程;
的方程;
(Ⅱ)定義:直線被曲線所截得的線段叫做這條曲線的弦。求曲線 的以
的以 (-3,1)為中點的弦的直線方程。
(-3,1)為中點的弦的直線方程。
21(本題滿分13分). 設函數 二次函數
二次函數 。
。
(Ⅰ)若 ,求
,求 的單調區間;
的單調區間;
(Ⅱ)當函數 與
與 的圖象只有一個公共點且
的圖象只有一個公共點且 存在最大值時,記
存在最大值時,記 的最大值為
的最大值為 ,求函數
,求函數 的解析式;
的解析式;
|
 與
與 在區間
在區間 內均為增函數,求實數
內均為增函數,求實數 的取值范圍。
的取值范圍。
株洲市2009年高三年級教學質量統一檢測(一)
15.設 分別是橢圓
分別是橢圓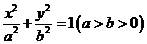 的左、右焦點,若在其左準線上存在點M,使線段MF2的中垂線過點F1,則橢圓的離心率的取值范圍是_______________.
的左、右焦點,若在其左準線上存在點M,使線段MF2的中垂線過點F1,則橢圓的離心率的取值范圍是_______________.
14.直線 按向量
按向量 平移后與圓
平移后與圓 相切,則實數
相切,則實數 的值為_____.
的值為_____.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com