
20.(16分)設函數f(x)=sin(2x+ )(-
)(- <
< <0),y=f(x)圖象的一條對稱軸是直線x=
<0),y=f(x)圖象的一條對稱軸是直線x= .
.
(1)求 ;
;
(2)求函數y=f(x)的單調增區間;
(3)證明:直線5x-2y+c=0與函數y=f(x)的圖象不相切.
(1)解 ∵x= 是函數y=f(x)的圖象的對稱軸,
是函數y=f(x)的圖象的對稱軸,
∴sin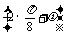 =±1,
=±1,
∴ +
+ =k
=k +
+ ,k∈Z.
,k∈Z.
∵- <
< <0,∴
<0,∴ =-
=- .
.
(2)解 由(1)知 =-
=- ,因此y=sin
,因此y=sin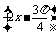 .
.
由題意得2k -
- ≤2x-
≤2x- ≤2k
≤2k +
+ ,k∈Z.
,k∈Z.
則k +
+ ≤x≤k
≤x≤k +
+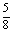
 ,k∈Z
,k∈Z
所以函數y=sin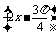 的單調增區間為
的單調增區間為
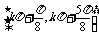 ,k∈Z.
,k∈Z.
(3)證明 ∵|y′|=|(sin(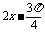 ))′|
))′|
=|2cos(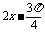 )|≤2,
)|≤2,
∴曲線y=f(x)的切線斜率的取值范圍是[-2,2],而直線5x-2y+c=0的斜率為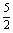 >2,所以直線5x-2y+c=0與函數
>2,所以直線5x-2y+c=0與函數
y=sin(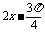 )的圖象不相切.
)的圖象不相切.
19.(16分)把曲線C:y=sin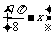 ·cos
·cos 向右平移a (a>0)個單位,得到的曲線C′關于直線x=
向右平移a (a>0)個單位,得到的曲線C′關于直線x= 對稱.
對稱.
(1)求a的最小值;
(2)就a的最小值證明:當x∈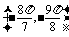 時,曲線C′上的任意兩點的直線斜率恒大于零.
時,曲線C′上的任意兩點的直線斜率恒大于零.
(1)解 ∵y=sin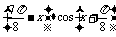
=sin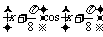
= sin
sin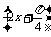 ,
,
∴曲線C′方程為y= sin
sin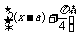 ,
,
它關于直線x= 對稱,
對稱,
∴ sin
sin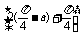 =±
=± ,
,
即2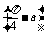 +
+ =k
=k +
+ (k∈Z),
(k∈Z),
解得a= -
-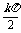 (k∈Z),
(k∈Z),
∵a>0,∴a的最小值是 .
.
(2)證明 當a= 時,曲線C′的方程為y=
時,曲線C′的方程為y= sin2x.
sin2x.
由函數y= sin2x的圖象可知:
sin2x的圖象可知:
當x∈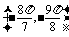 時,函數y=
時,函數y= sin2x是增函數,
sin2x是增函數,
所以當x1<x2時,有y1<y2,
所以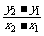 >0,即斜率恒大于零.
>0,即斜率恒大于零.
18.(16分)已知tan 、tan
、tan 是方程x2-4x-2=0的兩個實根,求:cos2(
是方程x2-4x-2=0的兩個實根,求:cos2( +
+ )+2sin(
)+2sin( +
+ )cos(
)cos( +
+ )-3sin2(
)-3sin2( +
+ )的值.
)的值.
解 由已知有tan +tan
+tan =4,tan
=4,tan ·tan
·tan =-2,
=-2,
∴tan( +
+ )=
)=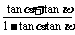 =
=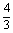 ,
,
cos2( +
+ )+2sin(
)+2sin( +
+ )cos(
)cos( +
+ )-3sin2(
)-3sin2( +
+ )
)
=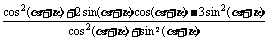
=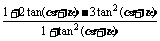
=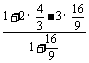 =-
=- .
.
17.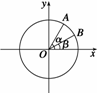 (2008·江蘇,15)(14分)如圖,在平面直角坐標系xOy中,以Ox軸為始邊作兩個銳角
(2008·江蘇,15)(14分)如圖,在平面直角坐標系xOy中,以Ox軸為始邊作兩個銳角 ,
,
 ,它們的終邊分別與單位圓相交于A,B兩點,已知A,B的橫坐標分別為
,它們的終邊分別與單位圓相交于A,B兩點,已知A,B的橫坐標分別為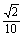 ,
,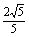 .
.
(1)求tan( +
+ )的值;
)的值;
(2)求 +2
+2 的值.
的值.
解 由條件得cos =
=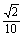 ,cos
,cos =
=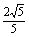 .
.
∵ ,
, 為銳角,
為銳角,
∴sin =
= =
=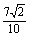 ,
,
sin =
=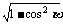 =
=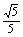 .
.
因此tan =
=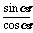 =7,tan
=7,tan =
=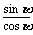 =
= .
.
(1)tan( +
+ )=
)=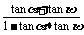 =
=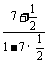 =-3.
=-3.
(2)∵tan2 =
=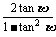 =
=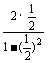 =
=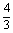 ,
,
∴tan( +2
+2 )=
)=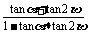 =
=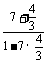 =-1.
=-1.
∵ ,
, 為銳角,∴0<
為銳角,∴0< +2
+2 <
<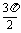 ,∴
,∴ +2
+2 =
= .
.
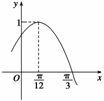
16.(14分)已知函數f(x)=Asin(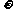 x+
x+ )(A>0,
)(A>0, 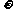 >0,|
>0,| |<
|< ) (x∈R)的部分圖象如圖所示.
) (x∈R)的部分圖象如圖所示.
(1)求f(x)的表達式;
(2)設g(x)=f(x)- f
f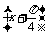 ,求函數g(x)的最小值及相應的x的取值集合.
,求函數g(x)的最小值及相應的x的取值集合.
解 (1)由圖象可知:A=1,
函數f(x)的周期T滿足: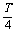 =
=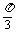 -
-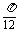 =
= ,T=
,T= ,
,
∴T=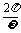 =
= .∴
.∴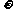 =2.∴f(x)=sin(2x+
=2.∴f(x)=sin(2x+ ).
).
又f(x)圖象過點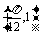 ,
,
∴f =sin
=sin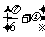 =1,
=1,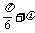 =2kπ+
=2kπ+ (k∈Z).
(k∈Z).
又| |<
|< ,故
,故 =
=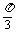 .∴f(x)=sin
.∴f(x)=sin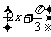 .
.
(2)方法一 g(x)=f(x)- f
f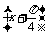
=sin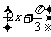 -
- sin
sin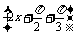
=sin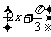 -
- sin
sin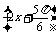
= sin2x+
sin2x+ cos2x+
cos2x+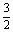 sin2x-
sin2x- cos2x
cos2x
=2sin2x,
由2x=2k -
- (k∈Z),得x=k
(k∈Z),得x=k -
- (k∈Z),
(k∈Z),
|
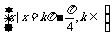 .
.
方法二 g(x)=f(x)- f
f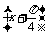
=sin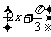 -
- sin
sin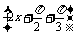
=sin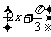 -
- cos
cos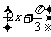
=2sin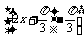 =2sin2x,
=2sin2x,
由2x=2k -
- (k∈Z),得x=k
(k∈Z),得x=k -
- (k∈Z),
(k∈Z),
∴g(x)的最小值為-2,相應的x的取值集合為{x|x=k -
- ,k∈Z}.
,k∈Z}.
15.(14分)已知 ∈
∈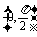 ,
, ∈
∈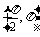 且sin(
且sin( +
+ )=
)=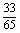 ,cos
,cos =-
=-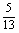 .求sin
.求sin .
.
解 ∵ ∈
∈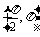 ,cos
,cos =-
=-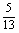 ,∴sin
,∴sin =
=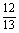 .
.
又∵0< <
< ,
, <
< <
< ,∴
,∴ <
< +
+ <
<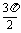 ,
,
又sin( +
+ )=
)=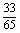 ,
,
∴ <
< +
+ <
< ,cos(
,cos( +
+ )=-
)=-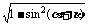
=-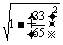 =-
=- ,
,
∴sin =sin[(
=sin[( +
+ )-
)- ]
]
=sin( +
+ )cos
)cos -cos(
-cos( +
+ )sin
)sin
 =
=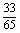 ·
· -
- ·
·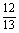 =
= .
.
14.關于函數f(x)=2sin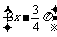 ,有下列命題:
,有下列命題:
①其最小正周期為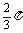 ;
;
②其圖象由y=2sin3x向左平移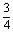 個單位而得到;
個單位而得到;
③在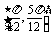 上為單調遞增函數,則其中真命題為
(寫出你認為正確答案的序號).
上為單調遞增函數,則其中真命題為
(寫出你認為正確答案的序號).
答案 ①③
13.若f(x)=asin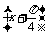 +bsin
+bsin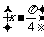 (ab≠0)是偶函數,則有序實數對(a,b)可以是
.(注:只要填滿足a+b=0的一組數字即可)
(ab≠0)是偶函數,則有序實數對(a,b)可以是
.(注:只要填滿足a+b=0的一組數字即可)
答案 (1,-1)
12.函數f(x)=sinx+2|sinx|,x∈[0,2 ]的圖象與直線y=k有且僅有兩個不同的交點,則k的取值范圍是 .
]的圖象與直線y=k有且僅有兩個不同的交點,則k的取值范圍是 .
答案 1<k<3
11.若cos( +
+ )=
)=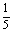 ,cos(
,cos( -
- )=
)= ,則tan
,則tan ·tan
·tan =
.
=
.
答案 
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com