
3. 已知函數(shù)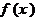 是定義在R上的奇函數(shù),當(dāng)
是定義在R上的奇函數(shù),當(dāng)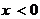 時(shí),
時(shí),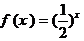 ,則
,則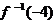 的值是( )
的值是( )
A.2
B.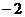 C.3 D.
C.3 D.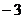
2.若不等式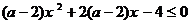 對(duì)一切
對(duì)一切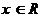 恒成立,則
恒成立,則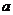 的取值范圍是 ( )
的取值范圍是 ( )
A.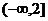 B.
B.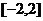 C.
C.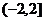 D.
D.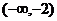
1.已知函數(shù)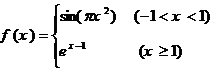 ,若
,若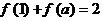 ,則
,則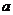 的所有可能值為( )
的所有可能值為( )
A.1
B.1或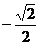 C.
C.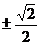 D. 1或
D. 1或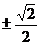
10.(2006北京)已知點(diǎn)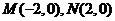 ,動(dòng)點(diǎn)
,動(dòng)點(diǎn)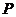 滿足條件
滿足條件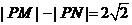 .記動(dòng)點(diǎn)
.記動(dòng)點(diǎn)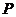 的軌跡為
的軌跡為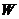 .
.
(Ⅰ)求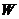 的方程;
的方程;
(Ⅱ)若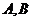 是
是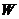 上的不同兩點(diǎn),
上的不同兩點(diǎn),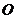 是坐標(biāo)原點(diǎn),求
是坐標(biāo)原點(diǎn),求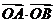 的最小值.
的最小值.
解法一:
(Ⅰ)由|PM|-|PN|=2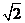 知?jiǎng)狱c(diǎn)P的軌跡是以M,N為焦點(diǎn)的雙曲線的右支,實(shí)半軸長(zhǎng)a=
知?jiǎng)狱c(diǎn)P的軌跡是以M,N為焦點(diǎn)的雙曲線的右支,實(shí)半軸長(zhǎng)a=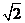 .
.
又半焦距c=2。故虛半軸長(zhǎng)b=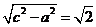 ,
,
所以W的方程為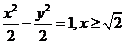
(Ⅱ)設(shè)A、B的坐標(biāo)分別為(x1y1),(x2y2).
當(dāng)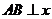 軸時(shí),
軸時(shí),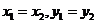 ,從而
,從而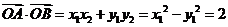 。
。
當(dāng)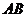 與
與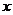 軸不垂直時(shí),設(shè)直線
軸不垂直時(shí),設(shè)直線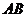 的方程為
的方程為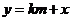 ,與
,與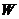 的方程聯(lián)立,消去
的方程聯(lián)立,消去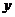 得
得
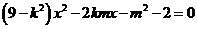 ,
,
故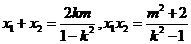
所以
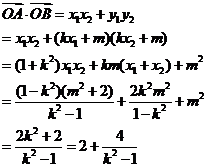
又因?yàn)?sub>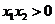 ,所以
,所以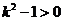 ,從而
,從而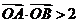 .
.
綜上,當(dāng)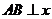 軸時(shí),
軸時(shí),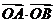 取得最小值2.
取得最小值2.
解法二:
(Ⅰ)同解法一.
(Ⅱ)設(shè)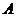 、
、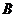 的坐標(biāo)分別為
的坐標(biāo)分別為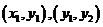 ,則
,則
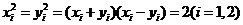
令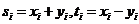 ,
,
則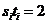 ,且
,且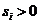 ,
,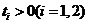 ,所以
,所以
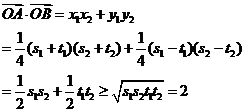
當(dāng)且僅當(dāng)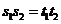 ,即
,即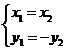 時(shí)“=”成立.
時(shí)“=”成立.
所以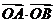 的最小值是2.
的最小值是2.
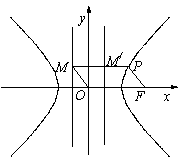
[探索題](2006安徽)如圖,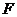 為雙曲線
為雙曲線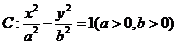 的右焦點(diǎn),
的右焦點(diǎn),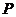 為雙曲線
為雙曲線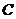 右支上一點(diǎn),且位于
右支上一點(diǎn),且位于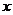 軸上方,
軸上方,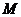 為左準(zhǔn)線上一點(diǎn),
為左準(zhǔn)線上一點(diǎn),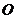 為坐標(biāo)原點(diǎn)。已知四邊形
為坐標(biāo)原點(diǎn)。已知四邊形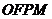 為平行四邊形,
為平行四邊形,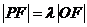 。
。
(Ⅰ)寫出雙曲線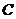 的離心率
的離心率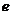 與
與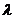 的關(guān)系式;
的關(guān)系式;
(Ⅱ)當(dāng)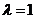 時(shí),經(jīng)過(guò)焦點(diǎn)
時(shí),經(jīng)過(guò)焦點(diǎn)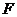 且平行于
且平行于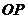 的直線交雙曲線于
的直線交雙曲線于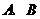 兩點(diǎn),若
兩點(diǎn),若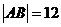 ,求此時(shí)的雙曲線方程。
,求此時(shí)的雙曲線方程。
(Ⅰ)解法1:設(shè)M′為PM與雙曲線右準(zhǔn)線的交點(diǎn),F(c,0),則
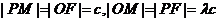

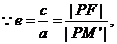
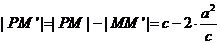
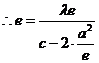
即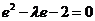
解法2:設(shè)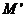 為
為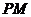 與雙曲線右準(zhǔn)線的交點(diǎn),N為左準(zhǔn)線與x軸的交點(diǎn).
與雙曲線右準(zhǔn)線的交點(diǎn),N為左準(zhǔn)線與x軸的交點(diǎn).
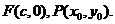 由于
由于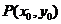 在雙曲線右支上,則
在雙曲線右支上,則
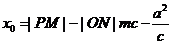 ①
①
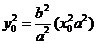 ②
②
由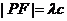 得
得
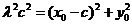 ③
③
將①、②代入③得
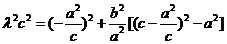
再將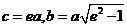 代入上式,得
代入上式,得
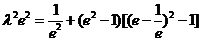
化簡(jiǎn),得
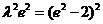 ④
④
由題意,點(diǎn)P位于雙曲線右支上,從而
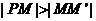
于是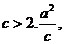 即
即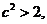 又
又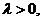 所以由④式得
所以由④式得
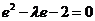
(Ⅱ)解:當(dāng)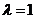 時(shí),由
時(shí),由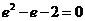 解得
解得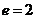
從而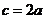 ,
,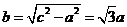
由此得雙曲線得方程是
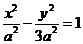
下面確定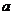 的值
的值
解法1:
設(shè)雙曲線左準(zhǔn)線與x軸的交點(diǎn)為N,P點(diǎn)的坐標(biāo)為(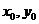 ),則
),則
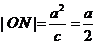 ,
,
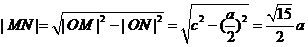
由于P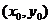 在雙曲線的右支上,且位于x軸上方,因而
在雙曲線的右支上,且位于x軸上方,因而
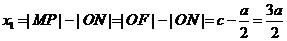 ,
,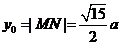
所以直線OP的斜率為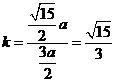
設(shè)過(guò)焦點(diǎn)F且平行于OP的直線與雙曲線的交點(diǎn)為A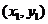 、B
、B ,則
,則
直線AB的斜線為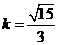 ,直線AB的方程為
,直線AB的方程為
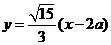
將其代入雙曲線方程整理得
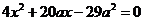
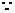
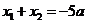 ,
,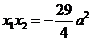
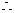
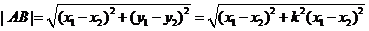
=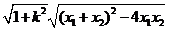
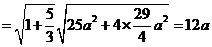
由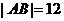 得
得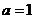 ,于是,所求雙曲線得方程為
,于是,所求雙曲線得方程為
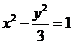
解法2.由條件知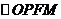 為菱形,其對(duì)角線OP與FM互相垂直平分,
為菱形,其對(duì)角線OP與FM互相垂直平分,
其交點(diǎn)Q為OP得中點(diǎn)
9.已知拋物線C:y2=4(x-1),橢圓C1的左焦點(diǎn)及左準(zhǔn)線與拋物線C的焦點(diǎn)F和準(zhǔn)線l分別重合.
(1)設(shè)B是橢圓C1短軸的一個(gè)端點(diǎn),線段BF的中點(diǎn)為P,求點(diǎn)P的軌跡C2的方程;
(2)如果直線x+y=m與曲線C2相交于不同兩點(diǎn)M、N,求m的取值范圍.
(1)解法一:由y2=4(x-1)知拋物線C的焦點(diǎn)F坐標(biāo)為(2,0).準(zhǔn)線l的方程為x=0.設(shè)動(dòng)橢圓C1的短軸的一個(gè)端點(diǎn)B的坐標(biāo)為(x1,y1)(x1>2,y1≠0),點(diǎn)P(x,y),
|
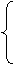
|
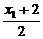 , x1=2x-2,
, x1=2x-2,
y=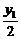 ,
y1=2y.
,
y1=2y.
∴B(2x-2,2y)(x>2,y≠0).
設(shè)點(diǎn)B在準(zhǔn)線x=0上的射影為點(diǎn)B′,橢圓的中心為點(diǎn)O′,則橢圓離心率e=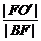 ,由
,由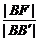 =
=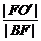 ,得
,得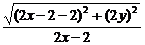 =
=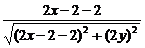 ,
,
整理,化簡(jiǎn)得y2=x-2(y≠0),這就是點(diǎn)P的軌跡方程.
解法二:拋物線y2=4(x-1)焦點(diǎn)為F(2,0),準(zhǔn)線l:x=0.設(shè)P(x,y),
∵P為BF中點(diǎn),
∴B(2x-2,2y)(x>2,y≠0).設(shè)橢圓C1的長(zhǎng)半軸、短半軸、半焦距分別為a、b、c,
則c=(2x-2)-2=2x-4,b2=(2y)2=4y2,
∵(-c)-(-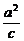 )=2,
)=2,
∴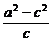 =2,
=2,
即b2=2c.∴4y2=2(2x-4),
即y2=x-2(y≠0),此即C2的軌跡方程.
|
|
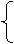 x+y=m,
x+y=m,
y2=x-2
m>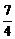 .
.
而當(dāng)m=2時(shí),直線x+y=2過(guò)點(diǎn)(2,0),這時(shí)它與曲線C2只有一個(gè)交點(diǎn),
∴所求m的取值范圍是(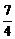 ,2)∪(2,+∞).
,2)∪(2,+∞).
8.(2006上海) 在平面直角坐標(biāo)系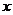 O
O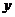 中,直線
中,直線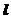 與拋物線
與拋物線 =2
=2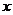 相交于A、B兩點(diǎn)
相交于A、B兩點(diǎn)
(1)求證:“如果直線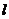 過(guò)點(diǎn)T(3,0),那么
過(guò)點(diǎn)T(3,0),那么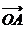
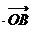 =3”是真命題;
=3”是真命題;
(2)寫出(1)中命題的逆命題,判斷它是真命題還是假命題,并說(shuō)明理由
[解](1)設(shè)過(guò)點(diǎn)T(3,0)的直線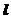 交拋物線y2=2x于點(diǎn)A(x1,y1)、B(x2,y2)
交拋物線y2=2x于點(diǎn)A(x1,y1)、B(x2,y2)
當(dāng)直線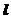 的鈄率不存在時(shí),直線
的鈄率不存在時(shí),直線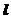 的方程為x=3,此時(shí),直線
的方程為x=3,此時(shí),直線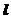 與拋物線相交于點(diǎn)A(3,
與拋物線相交于點(diǎn)A(3,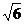 )、B(3,-
)、B(3,-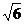 )
) ∴
∴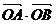 =3;
=3;
當(dāng)直線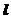 的鈄率存在時(shí),設(shè)直線
的鈄率存在時(shí),設(shè)直線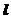 的方程為
的方程為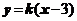 ,其中
,其中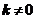 ,
,
由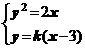 得
得 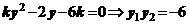
又 ∵
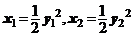 ,
,
∴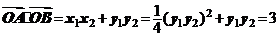 ,
,
綜上所述,命題“如果直線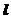 過(guò)點(diǎn)T(3,0),那么
過(guò)點(diǎn)T(3,0),那么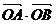 =3”是真命題;
=3”是真命題;
(2)逆命題是:設(shè)直線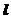 交拋物線y2=2x于A、B兩點(diǎn),如果
交拋物線y2=2x于A、B兩點(diǎn),如果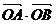 =3,那么該直線過(guò)點(diǎn)T(3,0)
=3,那么該直線過(guò)點(diǎn)T(3,0) 該命題是假命題
該命題是假命題
例如:取拋物線上的點(diǎn)A(2,2),B(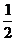 ,1),此時(shí)
,1),此時(shí)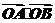 =3,
=3,
直線AB的方程為: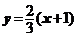 ,而T(3,0)不在直線AB上;
,而T(3,0)不在直線AB上;
說(shuō)明:由拋物線y2=2x上的點(diǎn)A (x1,y1)、B (x2,y2) 滿足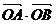 =3,可得y1y2=-6,
=3,可得y1y2=-6,
或y1y2=2,如果y1y2=-6,可證得直線AB過(guò)點(diǎn)(3,0);如果y1y2=2,可證得直線AB過(guò)點(diǎn)(-1,0),而不過(guò)點(diǎn)(3,0)
7. 正方形ABCD中,一條邊AB在直線y=x+4上,另外兩頂點(diǎn)C、D在拋物線y2=x上,求正方形的面積.
解:設(shè)CD所在直線的方程為y=x+t,
|
|
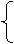 y=x+t,
y=x+t,
y2=x,
x2+(2t-1)x+t2=0,
∴|CD|=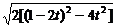
=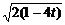 .
.
又直線AB與CD間距離為|AD|=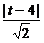 ,
,
∵|AD|=|CD|,
∴t=-2或-6.
從而邊長(zhǎng)為3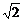 或5
或5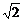 .
.
面積S1=(3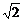 )2=18,S2=(5
)2=18,S2=(5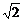 )2=50.
)2=50.
6.設(shè)過(guò)焦點(diǎn)F(1,0)的直線為y=k(x-1)(k≠0),A(x1,y1),B(x2,y2)
代入拋物線方程消去y得k2x2-2(k2+2)x+k2=0.
∵k2≠0,∴x1+x2=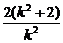 ,
,
|AB|=x1+x2+2=8, x1+x2=6. 可得k2=1.
∴△OAB的重心的橫坐標(biāo)為x=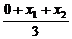 =2.
=2.
.法2:
由|AB|=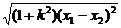 =8, 得k2=1…..
=8, 得k2=1…..
[解答題]
5.設(shè)直線l與橢圓交于P1(x1,y1)、P2(x2,y2),
將P1、P2兩點(diǎn)坐標(biāo)代入橢圓方程相減得直線l斜率
k=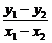 =-
=-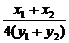 = -
= -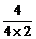 =-
=-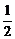 .
.
由點(diǎn)斜式可得l的方程為x+2y-8=0.
答案:x+2y-8=0
4.當(dāng)x>0時(shí),雙曲線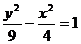 的漸近線為:
的漸近線為: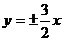 ,而直線y=x+3的斜率為1,1<3/2,因此直線與雙曲線的下支有一交點(diǎn),又y=x+3過(guò)橢圓
,而直線y=x+3的斜率為1,1<3/2,因此直線與雙曲線的下支有一交點(diǎn),又y=x+3過(guò)橢圓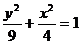 的頂點(diǎn),k=1>0因此直線與橢圓左半部分有一交點(diǎn),共計(jì)3個(gè)交點(diǎn),選D
的頂點(diǎn),k=1>0因此直線與橢圓左半部分有一交點(diǎn),共計(jì)3個(gè)交點(diǎn),選D
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com