日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

5．弦長公式：

圓錐曲線與直線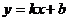交于A(x₁，y₁)，B(x₂，y₂)，則弦長

　 ；

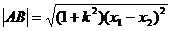與直線 A(x₁，y₁)，B(x₂，y₂)，則弦長

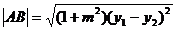
4．涉及直線與圓錐曲線相交弦的問題：

相交弦的長，弦所在直線的方程、弦的中點的軌跡等，這可以利用“點差法”，“設而不求”、 韋達定理、整體代入等方法求解。

3． 涉及到圓錐曲線焦點弦、焦半徑的問題，首先考慮第二定義和焦半徑公式。

2．直線與圓錐曲線有無公共點或有幾個公共點的問題：

可以轉化為它們所對應的方程構成的方程組是否有解或解的個數問題，往往通過消元轉化為討論一元二次方程的解的問題或一元二次函數的最值問題，運用韋達定理,中點公式,設而不求時必須Δ≥0,必須注意解的存在性和轉化的等價性，用好化歸與等價轉化思想．

當直線與拋物線的對稱軸平行或與雙曲線的漸近線平行時，消元后得到的是一元一次方程,只有一個解,即直線與拋物線或雙曲線有且只有一個交點．

1．直線與圓錐曲線的位置關系主要是：公共點、相交弦或焦點弦問題以及它們的綜合運用．

5．會利用“設點代點、設而不求”的方法求弦所在直線的方程(如中點弦、相交弦等)、弦的中點的軌跡等．

4．會用弦長公式|AB|=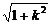|x₂－x₁|求弦的長；

3．會利用圓錐曲線的焦半徑公式解決焦點弦的問題 掌握求焦半徑以及利用焦半徑解題的方法;

2．會運用“設而不求”解決相交弦長問題及中點弦問題;

1．掌握直線與圓錐曲線公共點問題、相交弦問題以及它們的綜合應用解決這些問題經常轉化為它們所對應的方程構成的方程組是否有解或解的個數問題;