日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

4. 某班委會由4名男生與3名女生組成,現從中選出2人擔任正副班長,其中至少有1名女

生當選的概率是　　　　　　　　　　 (用分數作答)

3. 有紅、黃、藍三種顏色的旗幟各3面，在每種顏色的3面旗幟上分別標上號碼1、2和

3，現任取出3面，它們的顏色與號碼不相同的概率是　　　　　　　　 　　.

2. 種植兩株不同的花卉，它們的存活率分別為p和q，則恰有一株存活的概率為 (　　 )

(A)　 p+q－2p q 　　　　(B)　 p+q－pq　　　 (C) 　p+q　　　 (D)　 pq

1.　　　 一臺X型號自動機床在一小時內不需要工人照看的概率為0.8000,有四臺這中型號的自

動機床各自獨立工作,則在一小時內至多2臺機床需要工人照看的概率是 (　　 ) 　　　

(A)0.1536 　 　　(B) 0.1808 　 (C) 0.5632　　　 　　 (D) 0.9728

6.(Ⅰ)P(兩人都投進兩球)＝　 =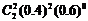　

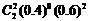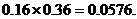
(Ⅱ)P(兩人至少投進三個球)＝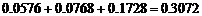

第二課時

例題

例1　 甲、乙二人參加普法知識競答，共有10個不同的題目，其中選擇題6個，判斷題4個，甲、乙二人依次各抽一題.

(Ⅰ)甲抽到選擇題、乙抽到判斷題的概率是多少？

(Ⅱ)甲、乙二人中至少有一人抽到選擇題的概率是多少？(2000年新課程卷)

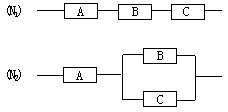
例2　 如圖,用A、B、C三類不同的元件連接成兩個系統N₁、N₂.當元件A、B、C都正常工作時,系統N₁正常工作；當元件A正常工作且元件B、C至少有一個正常工作時,系統N₂正常工作.已知元件A、B、C正常工作的概率依次為0.80,0.90,0.90.分別求系統N₁、N₂正常工作的概率P₁、P₂.　 (2001年新課程卷)

例3　 某單位6個員工借助互聯網開展工作，每個員工上網的概率都是0.5(相互獨立).

(Ⅰ)求至少3人同時上網的概率；

(Ⅱ)至少幾人同時上網的概率小于0.3？(2002年新課程卷)

例4　 有三種產品，合格率分別是0.90，0.95和0.95，各抽取一件進行檢驗.

(Ⅰ)求恰有一件不合格的概率；

(Ⅱ)求至少有兩件不合格的概率.(精確到0.001) (2003年新課程卷)

備用　 從分別寫有0，1，2，3，4，5，6的七張卡片中，任取4張，組成沒有重復數字的四位數，計算：

(1)這個四位數是偶數的概率；

(2)這個四位數能被9整除的概率；

(3)這個四位數比4510大的概率.

解： 　(1)組成的所有四位數共有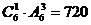個.四位偶數有：個位是0時有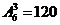,個位不是0時有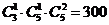,共有120+300=420個.

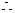組成的四位數為偶數的概率為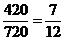

(2)能被9整除的數，應該各位上的數字和能被9整除.數字組合為：1，2，6，0　 1，3，5，0　 2，4，5，0　 3，4，5，6　 2，3，4，0　 此時共有.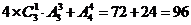

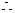能被9整除的四位數的概率為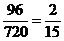

(3)比4510大的數分別有：千位是4，百位是5時，有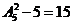;千位是4，百位是6時，有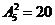;千位大于4時，有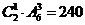;故共有240+20+18=278.

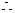四位數且比4510大的概率為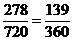

作業

5.(Ⅰ)P(A+B)= P(A)+P(B)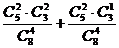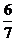＝=;　 (Ⅱ) P=-=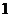

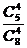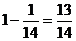
1. B　　　 2. 　D 　　　3.　 0.05　　　 4.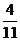 　

6.　　　　　 已知甲、乙兩人投籃的命中率分別為0.4和0.6．現讓每人各投兩次，試分別求下列事件的概率：(Ⅰ)兩人都投進兩球；(Ⅱ)兩人至少投進三個球.

作業答案

5.　 袋中有大小相同的5個白球和3個黑球，從中任意摸出4個，求下列事件發生的概率.

(Ⅰ)摸出2個或3個白球 ; (Ⅱ)至少摸出一個黑球.

4.　 若在二項式(x+1)¹⁰的展開式中任取一項,則該項的系數為奇數的概率是　 　　　.

(結果用分數表示)