
11.(2009浙江文)設等比數列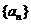 的公比
的公比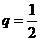 ,前
,前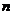 項和為
項和為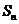 ,則
,則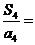 .
.
1.(2009年廣東卷文)已知等比數列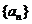 的公比為正數且
的公比為正數且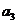 ·
· =2
=2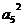
 =1則
=1則 = A
= A B
B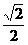 C
C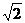 D.2
D.2
5.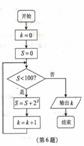 (浙江文6)某程序框圖如圖所示,該程序運行后輸出的k的值是A4
B5C6D7
(浙江文6)某程序框圖如圖所示,該程序運行后輸出的k的值是A4
B5C6D7
數列部分
17.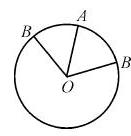 (2009福建卷文)點A為周長等于3的圓周上的一個定點,若在該圓周上隨機取一點B,則劣弧
(2009福建卷文)點A為周長等于3的圓周上的一個定點,若在該圓周上隨機取一點B,則劣弧 AB的長度小于1的概率為 。
AB的長度小于1的概率為 。
算法部分
14.(2009江蘇卷)某校甲、乙兩個班級各有5名編號為1,2,3,4,5的學生進行投籃練習,每人投10次,投中的次數如下表:
|
學生 |
1號 |
2號 |
3號 |
4號 |
5號 |
|
甲班 |
6 |
7 |
7 |
8 |
7 |
|
乙班 |
6 |
7 |
6 |
7 |
9 |
則以上兩組數據的方差中較小的一個為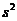 = .
= . 
13.(2009江蘇卷)現有5根竹竿,它們的長度(單位:m)分別為2.5,2.6,2.7,2.8,2.9,若從中一次隨機抽取2根竹竿,則它們的長度恰好相差0.3m的概率為 .
12.(2009安徽卷文)從長度分別為2、3、4、5的四條線段中任意取出三條,則以這三條線段為邊可以構成三角形的概率是________。
3.(2009山東卷文)在區間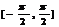 上隨機取一個數x,cosx的值介于0到
上隨機取一個數x,cosx的值介于0到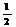 之間的概率為( ).A.
之間的概率為( ).A.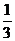 B.
B. C.
C. D.
D.
函數極限的求法及靈活應用是本講的難點,函數的極限大體有以下幾種類型:
(1)求函數值法--對于基本初等函數可采用
(2)“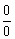 ”型--約去“零因子”(先分解因式),根式先有理化.
”型--約去“零因子”(先分解因式),根式先有理化.
②“ ”型--分子、分母同時除以分母的最高次冪;
”型--分子、分母同時除以分母的最高次冪;
③“∞-∞”型--根式分子有理化,或分解因式.
例4、求下列極限
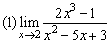
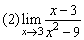
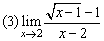

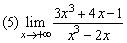
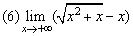
解:
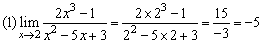 .
.
此法常用于f(x)在x=x0處及其附近有意義,且圖象在x=x0處不間斷.
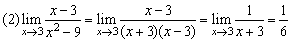 .
.
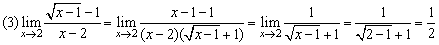 .
.
(2)(3)兩例的解法體現了對“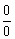 ”型極限計算的一種模式:對分子、分母作適當變形、分解或有理化,約去致使分母為0的公因式,然后再求極限.這里的關鍵是變形、分解或有理化,應注意對相關知識與技能的運用.
”型極限計算的一種模式:對分子、分母作適當變形、分解或有理化,約去致使分母為0的公因式,然后再求極限.這里的關鍵是變形、分解或有理化,應注意對相關知識與技能的運用.
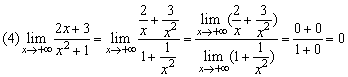 .
.
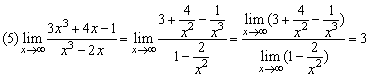 .
.
若a0≠0,b0≠0,m,n為正整數,則
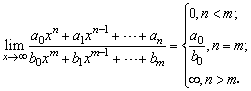
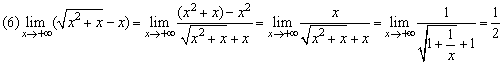 .
.
本題運用分子有理化技能,把“∞-∞型”極限計算轉化為“ 型”極限計算,進而利用(4)(5)的模式加以解決,這體現了轉化、化歸的思想,對這種思想應多領會、多運用.
型”極限計算,進而利用(4)(5)的模式加以解決,這體現了轉化、化歸的思想,對這種思想應多領會、多運用.
3、常用的函數極限
(1) (2)
(2)
(3) (4)
(4)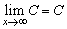
(5)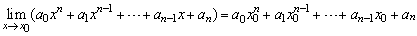
例1、判斷下列函數在指定處的極限是否存在:
(1)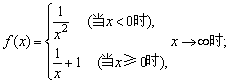
(2)
(3)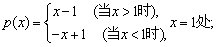
解:
(1)顯然,當x→-∞時,f(x)→0;當x→+∞時,f(x)→1.即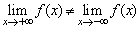 ,故
,故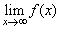 不存在.
不存在.
(2)顯然,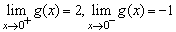 ,故
,故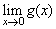 不存在.
不存在.
(3) .
.
例2、求下列各極限:
(1)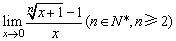 ;
;
(2)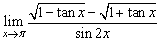
(3)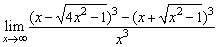 .
.
解:

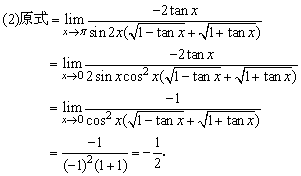

例3、求使下列各式成立的常數a、b的值:
(1) ;
;
(2)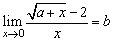 ;
;
(3) .
.
解:
(1)可令x2+ax+b=(x-2)(x+m),則由題意,得 ,于是
,于是 ,∴m=18,再由x2+ax+b=(x-2)(x+18),求得a=16,b=-36.
,∴m=18,再由x2+ax+b=(x-2)(x+18),求得a=16,b=-36.
(2)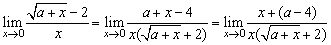 ,
,
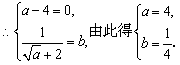
(3)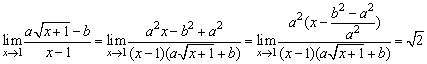
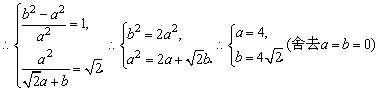
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com