日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

2、函數極限的運算法則

　如果，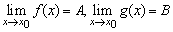

　那么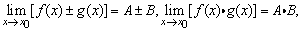

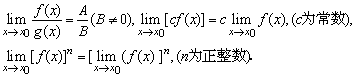
　說明：函數極限四則運算法則是以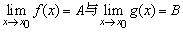為前提的．

　例如，求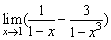時，就不能把它變成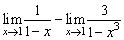，因為x→1時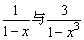，的極限均不存在．

　但．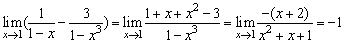

1、函數極限的概念

　(1)一般地，當自變量x取正值且無限增大時，如果函數y=f(x)的值無限趨近于一個常數A，就說當x趨向于正無窮大時，函數y=f(x)的極限是A，記作．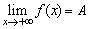

　(2)一般地，當自變量x取負值而|x|無限增大時，如果函數y=f(x)的值無限趨近于一個常數A，就說當x趨向于負無窮大時，函數y=f(x)的極限是A，記作．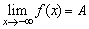

　(3)一般地，當自變量x的絕對值無限增大時，如果函數y=f(x)的值都無限趨近于一個常數A，就說當x趨向于無窮大時，函數y=f(x)的極限是A，記作．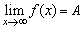

　(4)一般地，當自變量x無限趨近于常數x₀(但x≠x₀)時，如果函數y=f(x)無限趨近于一個常數A，就說當x趨向于x₀時，函數y=f(x)的極限是A，記作．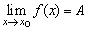

　說明：(1)我們常把(1)(2)稱為函數的單側極限，我們通常通過解析式或函數圖象來判斷函數單側極限，函數的單側極限不一定同時存在，例如，給定函數f(x)=2x，顯然當x→+∞時，2^x→+∞，即不存在，但．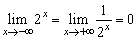

　(2)函數f(x)當x→x₀(或x→∞)時極限存在的必要且充分條件是：

　x→x₀⁺(或x→+∞)及x→x₀^－(或x→－∞)的極限各自存在并且相等，通常簡述為：左、右極限存在并且相等．

　(3)當x→x₀時f(x)在x₀處是否有定義無關，因為x→x₀并不要求x=x₀．

　(4)若函數f(x)在x=x₀處及其附近有意義，且圖象在x=x₀處不間斷，則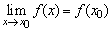．如．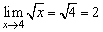

　本講在上講已經學習數列的極限的基礎上來學習函數的極限，主要探討函數極限的概念及函數極限的運算法則，學會求函數的極限．

8.(★★★★★)________,I have never seen anyone who’s as capable as John.

　　 A.As long as I have traveled

　　 B.Now that I have travelled so much

　　 C.Much as I have travelled

　　 D.As I have travelled so much

7.(★★★★★)So badly________ in the accident that he was sent to the nearest hospital immediately.

　　 A.he did injure B.he was injured

　　 C.did he injure D.was he injured

6.(★★★★)After that we never saw her again nor________ here.

　　 A.we heard B.have we heard

　　 C.we had heard D.did we hear

5.(★★★★★)-“It was cold yesterday.”

　　 -________.

　　 A.It was so B.So it was C.It did so D.So it did

4.(★★★★★)________that we can’t catch up with him.

　　 A.So fast did he run B.Fast as he ran

　　 C.Fast he ran so D.He ran fast

3.(★★★★★)Now________ to look after the wounded.

　　es my turn

　　 C.my turn came D.my turn is coming

2.(★★★★★)Autumn coming,down________.

　　 A.the leaves full B.leaves falling

　　 C.fall the leaves D.so the leaves full