
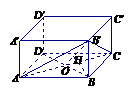
3.已知:正四棱柱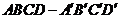 的底面邊長為
的底面邊長為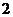 ,側棱長為
,側棱長為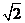 ,
,
(1)求二面角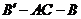 的大小;(2)求點
的大小;(2)求點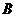 到平面
到平面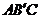 的距離
的距離
17.棱柱的側面積是指所有側面面積之和: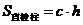 (
(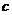 為底面周長,
為底面周長,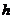 是高,即直棱柱的側棱長)
是高,即直棱柱的側棱長)
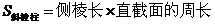
 18.棱柱的體積:
18.棱柱的體積: 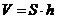

練習:
 1
1 ?判斷下列結論是否正確,為什么?(1)有一個面是多邊形,其余各面是三角形的幾何體是棱錐;
?判斷下列結論是否正確,為什么?(1)有一個面是多邊形,其余各面是三角形的幾何體是棱錐;
(2)正四面體是四棱錐;(3)側棱與底面所成的角相等的棱錐是正棱錐;
(4)側棱長相等,各側面與底面所成的角相等的棱錐是正棱錐.
2  如圖平行六面體
如圖平行六面體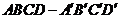 中,
中, ,
,
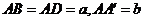 ,求對角面
,求對角面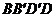 的面積
的面積
16.正多面體共有五種:正四面體、正六面體、正八面體、正十二面體、正二十面體.





以上五種正多面體的表面展開圖如下:

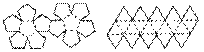

15.正多面體是一種特殊的凸多面體,它有兩個特點:①每個面都是有相同邊數的正多邊形;②每個頂點處都有相同數目的棱.正多面體的各個面是全等的正多邊形,各條棱是相等的線段.
14.正多面體:每個面都是有相同邊數的正多邊形,每個頂點為端點都有相同棱數的凸多面體.
13.正棱錐:底面是正多邊形,頂點在底面上的射影是底面的中心的棱錐叫正棱錐.(1)正棱錐的各側棱相等,各側面是全等的等腰三角形,各等腰三角形底邊上的高相等(叫正棱錐的斜高).(2)正棱錐的高、斜高、斜高在底面上的射影組成一個直角三角形;正棱錐的高、側棱、側棱在底面上的射影也組成一個直角三角形
12. 棱錐的性質:如果棱錐被平行于底面的平面所截,那么所得的截面與底面相似,截面面積與底面面積比等于頂點到截面的距離與棱錐高的平方比.
棱錐的性質:如果棱錐被平行于底面的平面所截,那么所得的截面與底面相似,截面面積與底面面積比等于頂點到截面的距離與棱錐高的平方比.
中截面:經過棱錐高的中點且平行于底面的截面,叫棱錐的中截面
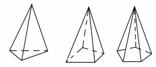
11.棱錐的分類:(按底面多邊形的邊數)
分別稱底面是三角形,四邊形,五邊形……的棱錐為三棱錐,四棱錐,五棱錐……(如圖)
10.棱錐的表示:棱錐用頂點和底面各頂點的字母,或用頂點和底面一條對角線端點的字母來表示
如圖棱錐可表示為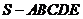 ,或
,或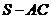 .
.
8.平行六面體、長方體的性質:(1)平行六面體的對角線交于一點,對角線 相交于一點,且在點
相交于一點,且在點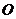 處互相平分.(2)長方體的一條對角線長的平方等于一個頂點上的三條棱長的平方和
處互相平分.(2)長方體的一條對角線長的平方等于一個頂點上的三條棱長的平方和
 9
9  棱錐的概念:有一個面是多邊形,其余各面是有一個公共頂點的三角形,這樣的多面體叫棱錐
棱錐的概念:有一個面是多邊形,其余各面是有一個公共頂點的三角形,這樣的多面體叫棱錐 其中有公共頂點的三角形叫棱錐的側面;多邊形叫棱錐的底面或底;各側面的公共頂點
其中有公共頂點的三角形叫棱錐的側面;多邊形叫棱錐的底面或底;各側面的公共頂點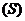 ,叫棱錐的頂點,頂點到底面所在平面的垂線段
,叫棱錐的頂點,頂點到底面所在平面的垂線段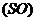 ,叫棱錐的高(垂線段的長也簡稱高).
,叫棱錐的高(垂線段的長也簡稱高).
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com