日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

5.　 已知10件產品中有3件是次品.

　　　 (I)任意取出3件產品作檢驗，求其中至少有1件是次品的概率；

　　　 (II)為了保證使3件次品全部檢驗出的概率超過0.6，最少應抽取幾件產品作檢驗？

4.　 某國際科研合作項目成員由11個美國人、4個法國人和5個中國人組成。現從中隨機

選出兩位作為成果發布人，則此兩人不屬于同一個國家的概率為　　　　　　　　

(結果用分數表示)

3.　 在某次花樣滑冰比賽中，發生裁判受賄事件，競賽委員會決定將裁判曰原來的9名增至14名，但只任取其中7名裁判的評分作為有效分，若14名裁判中有2人受賄，則有效分中沒有受賄裁判的評分的概率是　　　　.(結果用數值表示)

2.　 在5張卡片上分別寫著數字1、2、3、4、5，然后把它們混合，再任意排成一行，則得到的數能被5或2整除的概率是(　　 )

(A) 0.8　　　　　 (B) 0.6　　　　　 (C) 0.4　　　　　 (D) 0.2

1.　　　 將一顆質地均勻的骰子(它是一種各面上分別標有點數1，2，3，4，5，6的正方體玩

具)先后拋擲3次，至少出現一次6點向上的概率是 (　　 )　　

(A)　　　　(B)　　　　　(C)　　　　　(D)

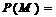
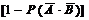
6．解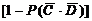： =0.752

第三課時

例題

例1 　從10位同學(其中6女，4男)中隨機選出3位參加測驗.每位女同學能通過測驗的概率均為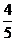，每位男同學能通過測驗的概率均為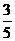.試求：

(Ⅰ)選出的3位同學中，至少有一位男同學的概率；

(Ⅱ)10位同學中的女同學甲和男同學乙同時被選中且通過測驗的概率.

　(2004年全國卷Ⅰ)

例2 　已知8支球隊中有3支弱隊,以抽簽方式將這8支球隊分為A、B兩組,每組4支.求：

(Ⅰ)A、B兩組中有一組恰有兩支弱隊的概率；

(Ⅱ)A組中至少有兩支弱隊的概率.　 　(2004年全國卷Ⅱ)

例3　 某同學參加科普知識競賽，需回答3個問題.競賽規則規定：答對第一、二、三問題分別得100分、100分、200分，答錯得零分.假設這名同學答對第一、二、三個問題的概率分別為0.8、0.7、0.6，且各題答對與否相互之間沒有影響.

(Ⅰ)求這名同學得300分的概率；

(Ⅱ)求這名同學至少得300分的概率.　 (2004年全國卷Ⅲ)

例4　 從4名男生和2名女生中任選3人參加演講比賽.

(Ⅰ)求所選3人都是男生的概率；

(Ⅱ)求所選3人中恰有1名女生的概率；

(Ⅲ)求所選3人中至少有1名女生的概率.　 (2004年天津卷)

備用 　A、B、C、D、E五人分四本不同的書，每人至多分一本，求：

(1)A不分甲書，B不分乙書的概率；

(2)甲書不分給A、B，乙書不分給C的概率.

解： (1)分別記“分不到書的是A，B不分乙書”，“分不到書的是B，A不分甲書”，“分不到書的是除A,B以外的其余的三人中的一人，同時A不分甲書，B不分乙書”為事件A₁,B₁,C₁，它們的概率是

.

因為事件A₁,B₁,C₁彼此互斥，由互斥事件的概率加法公式，A不分甲書，B不分乙書的概率是：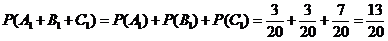

(2) 在乙書不分給C的情況下，分別記“甲書分給C”，“甲書分給D”，“甲書分給E”為事件A₂,B₂,C₂彼此互斥，有互斥事件的概率加法公式，甲書不分給A,B，乙書不分給C的概率為：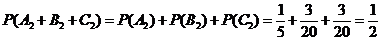

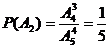
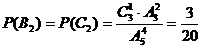
作業

1. D 　　2. A　 3.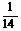　 4. 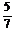　　5．解：有兩種可能：將原1件次品仍鑒定為次品，原3件正品中1件錯誤地鑒定為次品;將原1件次品錯誤地鑒定為正品，原3件正品中的2件錯誤地鑒定為次品.　 概率為

P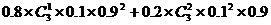＝＝0.1998

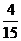1. (Ⅰ) ; (Ⅱ)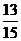.　　 2. 0.648; 0.792. 　　3. (Ⅰ) 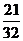; (Ⅱ) 5人.　 　4. (Ⅰ) 0.176 ; (Ⅱ) 0.012 .

作業答案

6.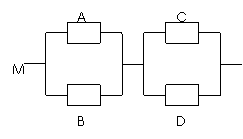 如圖，用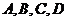表示四類不同的元件連接成系統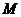.當元件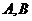至少有一個正常工作且元件至少有一個正常工作時，系統

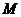
正常工作.已知元件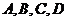正常工作的概率

依次為0.5，0.6，0.7，0.8，求元件連接成的系

統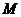正常工作的概率.

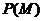例題答案

5. 某產品檢驗員檢查每一件產品時，將正品錯誤地鑒定為次品的概率為0.1，將次口錯誤地鑒定為正品的概率為0.2，如果這位檢驗員要鑒定4件產品，這4件產品中3件是正品，1件是次品，試求檢驗員鑒定成正品，次品各2件的概率.