
1.(Ⅰ)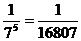 ; (Ⅱ)
; (Ⅱ)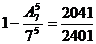 . 2.(Ⅰ)
. 2.(Ⅰ)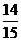 ;(Ⅱ)
;(Ⅱ)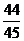 .
.
6. 甲、乙、丙三人分別獨立解一道題,已知甲做對這道題的概率是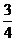 ,甲、丙兩人都做錯的概率是
,甲、丙兩人都做錯的概率是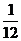 ,乙、丙兩人都做對的概率是
,乙、丙兩人都做對的概率是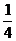 .
.
(Ⅰ)求乙、丙兩人各自做對這道題的概率;
(Ⅱ)求甲、乙、丙三人中至少有兩人做對這道題的概率.
例題答案
5. 張華同學騎自行車上學途中要經過4個交叉路口,在各交叉路口遇到紅燈的概率都是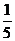 (假設各交叉路口遇到紅燈的事件是相互獨立的).
(假設各交叉路口遇到紅燈的事件是相互獨立的).
(Ⅰ)求張華同學某次上學途中恰好遇到3次紅燈的概率.
(Ⅱ)求張華同學某次上學時,在途中首次遇到紅燈前已經過2 個交叉路口的概率.設
4. 口袋內裝有10個相同的球,其中5個球標有數字0,5個球標有數字1,若從袋中摸出
5個球,那么摸出的5個球所標數字之和小于2或大于3的概率是 .(以數值作答)
3. 一個袋中有帶標號的7個白球,3個黑球.事件A:從袋中摸出兩個球,先摸的是黑球,
后摸的是白球.那么事件A發生的概率為________.
2. 甲、乙兩人獨立地解同一題,甲解決這個問題的概率是0.4,乙解決這個問題的概率是0.5,那么其中至少有一人解決這個問題的概率是 ( )
(A)0.9 (B)0.2 (C)0.8 (D)0.7
1. 從1,2,…,9這九個數中,隨機抽取3個不同的數,則這3個數的和為偶數的概率是
(A)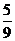 (B)
(B)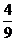 (C)
(C)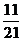 (D)
(D)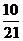 ( )
( )
6. 解:(I)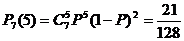 . (II)P6(5)+P5(5)+P4(4)
=C65P5(1-P)+C55P5+C44P4=
. (II)P6(5)+P5(5)+P4(4)
=C65P5(1-P)+C55P5+C44P4=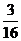
第四課時
例題
例1 某地區有5個工廠,由于用電緊缺,規定每個工廠在一周內必須選擇某一天停電
(選哪一天是等可能的).假定工廠之間的選擇互不影響.
(Ⅰ)求5個工廠均選擇星期日停電的概率;
(Ⅱ)求至少有兩個工廠選擇同一天停電的概率. (2004年浙江卷)
例2 甲、乙兩人參加一次英語口語考試,已知在備選的10道試題中,甲能答對其中的6題,乙能答對其中的8題.規定每次考試都從備選題中隨機抽出3題進行測試,至少答對2題才算合格.
(Ⅰ)分別求甲、乙兩人考試合格的概率;
(Ⅱ)求甲、乙兩人至少有一人考試合格的概率. (2004年福建卷)
例3 甲、乙、丙三臺機床各自獨立地加工同一種零件,已知甲機床加工的零件是一等品而乙機床加工的零件不是一等品的概率為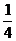 ,乙機床加工的零件是一等品而丙機床加工的零件不是一等品的概率為
,乙機床加工的零件是一等品而丙機床加工的零件不是一等品的概率為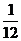 ,甲、丙兩臺機床加工的零件都是一等品的概率為
,甲、丙兩臺機床加工的零件都是一等品的概率為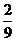 .
.
(Ⅰ)分別求甲、乙、丙三臺機床各自加工零件是一等品的概率;
(Ⅱ)從甲、乙、丙加工的零件中各取一個檢驗,求至少有一個一等品的概率.
(2004年湖南卷)
例4 為防止某突發事件發生,有甲、乙、丙、丁四種相互獨立的預防措施可供采用,單獨采用甲、乙、丙、丁預防措施后此突發事件不發生的概率(記為P)和所需費用如下:
|
預防措施 |
甲 |
乙 |
丙 |
丁 |
|
P |
0.9 |
0.8 |
0.7 |
0.6 |
|
費用(萬元) |
90 |
60 |
30 |
10 |
預防方案可單獨采用一種預防措施或聯合采用幾種預防措施,在總費用不超過120萬元的前提下,請確定一個預防方案,使得此突發事件不發生的概率最大.(2004年湖北卷)
備用 一個醫生已知某種疾病患者的痊愈率為25%,為實驗一種新藥是否有效,把它給10個病人服用,且規定若10個病人中至少有4個被治好,則認為這種藥有效;反之,則認為無效,試求:
(1)雖新藥有效,且把痊愈率提高到35%,但通過試驗被否定的概率;
(2)新藥完全無效,但通過試驗被認為有效的概率.
解: 記一個病人服用該藥痊愈為事件 A,且其概率為P,那么10個病人服用該藥相當于10次重復試驗.
(1)因新藥有效且P=0.35,故由n次獨立重復試驗中事件A發生k次的概率公式知,試驗被否定(即新藥無效)的概率為
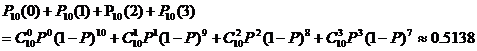
(2)因新藥無效,故P=0.25,試驗被認為有效的概率為
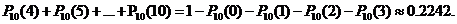
答: 新藥有效,但通過試驗被否定的概率為0.5138;而新藥無效,但通過試驗被認為有效的概率為0.2242
作業
1. D 2. B 3. 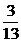 4.
4. 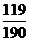 5. 解:(Ⅰ)
5. 解:(Ⅰ)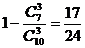 (Ⅱ)最少應抽取9件產品作檢驗.
(Ⅱ)最少應抽取9件產品作檢驗.
6. 冰箱中放有甲、乙兩種飲料各5瓶,每次飲用時從中任意取1瓶甲種或乙種飲料,取用甲種或乙種飲料的概率相等.
(Ⅰ)求甲種飲料飲用完畢而乙種飲料還剩下3瓶的概率;
(Ⅱ)求甲種飲料被飲用瓶數比乙種飲料被飲用瓶數至少多4瓶的概率.
例題答案
1(Ⅰ)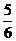 ;(Ⅱ)
;(Ⅱ)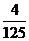 2(Ⅰ)
2(Ⅰ)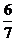 ;(Ⅱ)
;(Ⅱ)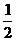 . 3(Ⅰ)0.228;(Ⅱ)0.564. 4(Ⅰ)
. 3(Ⅰ)0.228;(Ⅱ)0.564. 4(Ⅰ)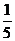 ;(Ⅱ)
;(Ⅱ)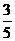 ;(Ⅲ)
;(Ⅲ)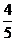 .
.
作業答案
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com