
4.若 是奇函數,且當
是奇函數,且當 >0時,
>0時,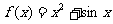 ,則當
,則當
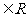 時,
時, 為( C )
為( C )
(A) (B)
(B) (C)|
(C)| |
|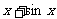 (D)|
(D)| |
|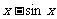
3.已知函數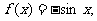 ,則下面三個命題中:(1)
,則下面三個命題中:(1)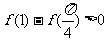 ;(2)
;(2)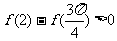 ;(3)
;(3)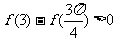 ;其中正確的命題共有( B )
;其中正確的命題共有( B )
(A) 0個 (B) 1個 (C)2個 (D)3個
2.為了得到函數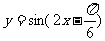 的圖象,可以將函數
的圖象,可以將函數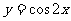 的圖象(B )
的圖象(B )
(A)向右平移 個單位長度 (B)向右平移
個單位長度 (B)向右平移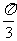 個單位長度
個單位長度
(C)向左平移 個單位長度 (D)向左平移
個單位長度 (D)向左平移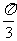 個單位長度
個單位長度
1.若 ,則滿足
,則滿足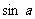 =0.5的角
=0.5的角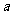 的個數是(C)
的個數是(C)
(A)2 (B)3 (C) 4 (D)5
例5. 求函數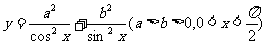 的最小值。
的最小值。
錯解 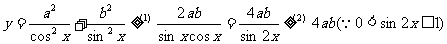
∴當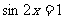 時,
時,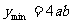
分析:在已知條件下,(1)、(2)兩處不能同時取等號。
正解: 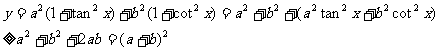
當且僅當 ,即
,即 ,時,
,時,
專題四:三角函數
[經典題例]
例1:點P從(1,0)出發,沿單位圓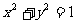 逆時針方向運動
逆時針方向運動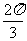 弧長到達Q點,則Q點的坐標為( )
弧長到達Q點,則Q點的坐標為( )
(A)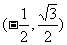 (B)
(B)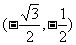 (C)
(C)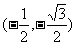 (D)
(D)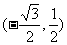
[思路分析] 記 ,由三角函數定義可知Q點的坐標
,由三角函數定義可知Q點的坐標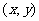 滿足
滿足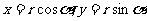 ,故選(A)
,故選(A)
[簡要評述]三角函數定義是三角函數理論的基礎,理解掌握能起到事半功倍的效果。
例2:求函數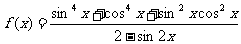 的最小正周期、最大值和最小值.
的最小正周期、最大值和最小值.
[思路分析]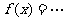
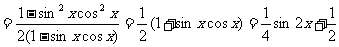
所以函數f(x)的最小正周期是π,最大值是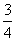 ,最小值是
,最小值是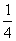 .
.
[簡要評述]三角恒等變形是歷年高考考察的主要內容,變形能力的提高取決于一定量的訓練以及方法的積累,在此例中“降次、化同角”是基本的思路。此外,求函數的周期、最值是考察的熱點,變形化簡是必經之路。
例3:已知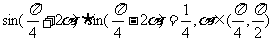 ,
,
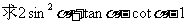 的值.
的值.
[思路分析] ∵ 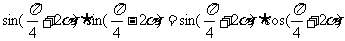
 ∴得
∴得 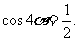 又
又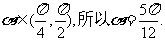
于是 
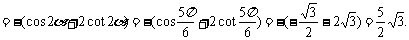
[簡要評述] 此類求值問題的類型是:已知三角方程,求某三角代數式的值。一般來說先解三角方程,得角的值或角的某個三角函數值。如何使解題過程化繁為簡,變形仍然顯得重要,此題中巧用誘導公式、二倍角公式,還用到了常用的變形方法,即“化正余切為正余弦”。
例4:已知b、c是實數,函數f(x)= 對任意α、β
對任意α、β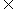 R有:
R有: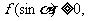
且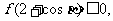
(1)求f(1)的值;(2)證明:c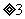 ;(3)設
;(3)設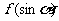 的最大值為10,求f(x)。
的最大值為10,求f(x)。
[思路分析](1)令α=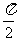 ,得
,得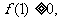 令β=
令β=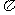 ,得
,得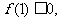 因此
因此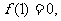 ;
;
(2)證明:由已知,當 時,
時,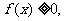 當
當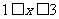 時,
時,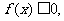 通過數形結合的方法可得:
通過數形結合的方法可得: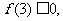 化簡得c
化簡得c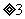 ;
;
(3)由上述可知,[-1,1]是 的減區間,那么
的減區間,那么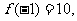 又
又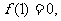 聯立方程組可得
聯立方程組可得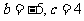 ,所以
,所以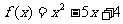
[簡要評述]三角復合問題是綜合運用知識的一個方面,復合函數問題的認識是高中數學學習的重點和難點,這一方面的學習有利于提高綜合運用的能力。
例5:關于正弦曲線回答下述問題:
(1)函數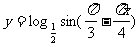 的單調遞增區間是
的單調遞增區間是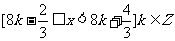 ;
;
(2)若函數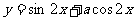 的圖象關于直線
的圖象關于直線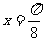 對稱,則
對稱,則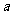 的值是 1 ;
的值是 1 ;
(3)把函數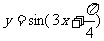 的圖象向右平移
的圖象向右平移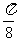 個單位,再將圖象上各點的橫坐標擴大到原來的3倍(縱坐標不變),則所得的函數解析式子是
個單位,再將圖象上各點的橫坐標擴大到原來的3倍(縱坐標不變),則所得的函數解析式子是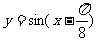 ;
;
(4)若函數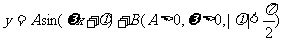 的最大值是
的最大值是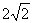 ,最小值是
,最小值是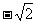 ,最小正周期是
,最小正周期是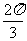 ,圖象經過點(0,-
,圖象經過點(0,-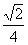 ),則函數的解析式子是
),則函數的解析式子是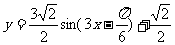 ;
;
[思路分析] 略
[簡要評述]正弦曲線問題是三角函數性質、圖象問題中的重點內容,必須熟練掌握。上述問題的解答可以根據正弦曲線的“五點畫法”在草稿紙上作出函數的草圖來驗證答案或得到答案。
例6:函數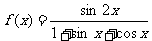
(1)求f(x)的定義域;(2)求f(x)的最大值及對應的x值。
[思路分析] (1){x|x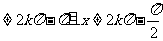
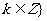
(2)設t=sinx+cosx, 則y=t-1 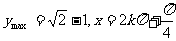
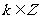
[簡要評述]若 關于
關于 與
與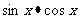 的表達式,求函數的最值常通過換元法,如令
的表達式,求函數的最值常通過換元法,如令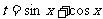 ,使問題得到簡化。
,使問題得到簡化。
例7:在ΔABC中,已知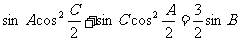 (1)求證:a、b、c成等差數列;(2)求角B的取值范圍。
(1)求證:a、b、c成等差數列;(2)求角B的取值范圍。
[思路分析](1)條件等式降次化簡得
(2)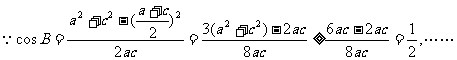
∴……,得B的取值范圍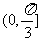
[簡要評述]三角形中的變換問題,除了需要運用三角式變換的所有方法、技巧外,還經常需要考慮對條件或結論中的“邊”與“角”運用“正弦定理、余弦定理或面積公式”進行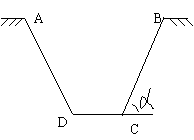 互換。
互換。
例8:水渠橫斷面為等腰梯形,如圖所示,渠道深為h,梯形面積為S,為了使渠道的滲水量達到最小,應使梯形兩腰及下底之和達到最小,此時下底角α應該是多少?
[思路分析] CD=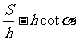 , C=
, C= ,轉化為考慮y=
,轉化為考慮y=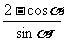 的最小值,可得當
的最小值,可得當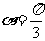 時,y最小,即C最小。
時,y最小,即C最小。
[簡要評述]“學以致用”是學習的目的之一,三角知識的應用很廣泛,在復習過程中應受到重視。
[熱身沖刺]
例4. 設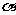 、
、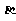 為銳角,且
為銳角,且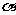 +
+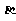
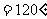 ,討論函數
,討論函數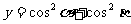 的最值。
的最值。
錯解 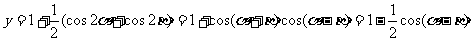
可見,當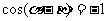 時,
時,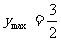 ;當
;當 時,
時,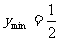 。
。
分析:由已知得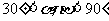 ,∴
,∴ ,則
,則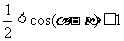
∴當 ,即
,即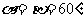 時,
時,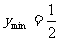 ,最大值不存在。
,最大值不存在。
例3. 若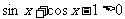 ,求
,求 的取值范圍。
的取值范圍。
錯解 移項得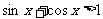 ,兩邊平方得
,兩邊平方得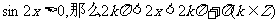
即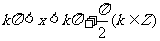
分析:忽略了滿足不等式的 在第一象限,上述解法引進了
在第一象限,上述解法引進了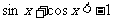 。
。
正解: 即
即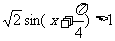 ,由
,由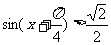 得
得
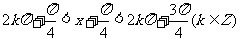 ∴
∴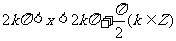
例2. 已知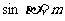 ,求
,求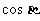 的值及相應
的值及相應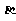 的取值范圍。
的取值范圍。
錯解 當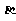 是第一、四象限時,
是第一、四象限時,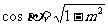 ,當
,當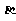 是第二、三象限時,
是第二、三象限時,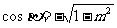 。
。
分析:把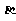 限制為象限角時,只考慮
限制為象限角時,只考慮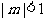 且
且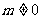 的情形,遺漏了界限角。應補充:當
的情形,遺漏了界限角。應補充:當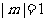 時,
時,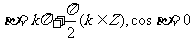 ;當
;當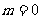 時,
時,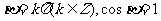 ,或
,或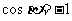 。
。
例1. 若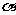 、
、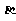 為第三象限角,且
為第三象限角,且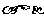 ,則( )
,則( )
(A)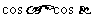 (B)
(B)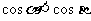 (C)
(C)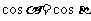 (D)以上都不對
(D)以上都不對
錯解 選(A)
分析:角的概念不清,誤將象限角看成類似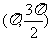 區間角。如取
區間角。如取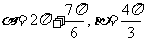 ,可知(A)不對。用排除法,可知應選(D)。
,可知(A)不對。用排除法,可知應選(D)。
20.設平面上有直線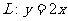 ,曲線
,曲線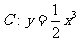 。又有下列方式定義數列
。又有下列方式定義數列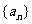 :
:
(1)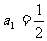 ;(2)當給定
;(2)當給定 后,作過點
后,作過點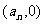 且與
且與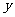 軸平行的直線,它與
軸平行的直線,它與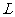 的交點記為
的交點記為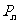 ;再過點
;再過點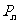 且與
且與 軸平行的直線,它與
軸平行的直線,它與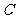 的交點記為
的交點記為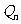 ,定義
,定義 為
為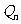 的橫坐標。試求數列
的橫坐標。試求數列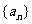 的通項,并計算
的通項,并計算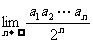 。
。
解:顯然,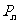 的坐標可寫為
的坐標可寫為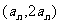 ,
,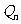 的坐標寫為
的坐標寫為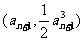 ,故有
,故有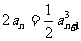 ,
,
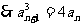 ,兩邊取對數并整理得:
,兩邊取對數并整理得: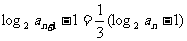 , 從而得
, 從而得
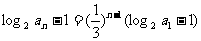 ,即
,即 ,
,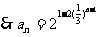 ,
,
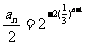 ,
,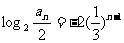 ,
,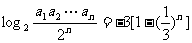 ,
,
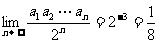 。
。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com