
19.設函數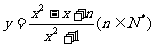 的最小值為
的最小值為 ,最大值為
,最大值為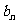 ,且
,且 。
。
(1)求數列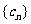 的通項公式;
的通項公式;
(2)設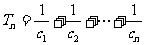 ,求證:
,求證: 。
。
解:(1)由已知函數式可得,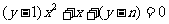 ,由已知可知
,由已知可知 ,令
,令 ,得
,得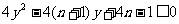 ,
, 已知函數最小值為
已知函數最小值為 ,最大值為
,最大值為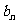 ,
,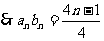 ,
,
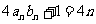 ,
,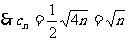 。
。
(2) ,
,
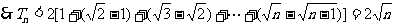 。
。
又 ,
,
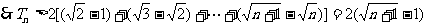 。
。
因此, 。
。
18.假設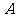 型汽車關稅在
型汽車關稅在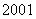 年是
年是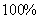 ,在
,在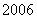 年是
年是 ,
,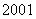 年
年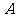 型進口車每輛價格為
型進口車每輛價格為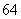 萬元(其中含
萬元(其中含 萬元關稅稅款)。
萬元關稅稅款)。
(1)已知與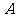 型車性能相近的
型車性能相近的 型國產車,
型國產車,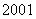 年的價格為
年的價格為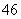 萬元,若
萬元,若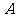 型車的價格只受關稅降低的影響,為了保證在
型車的價格只受關稅降低的影響,為了保證在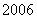 年
年 型車的價格不高于
型車的價格不高于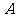 型車價格的
型車價格的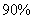 ,
, 型車的價格要逐年降低,問平均每年至少下降多少萬元?
型車的價格要逐年降低,問平均每年至少下降多少萬元?
(2)某人在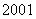 年將
年將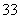 萬元存入銀行,假設該銀行扣利息稅后的年利率為
萬元存入銀行,假設該銀行扣利息稅后的年利率為 (五年內不變),且每年按復利計算(例如,第一年的利息記入第
(五年內不變),且每年按復利計算(例如,第一年的利息記入第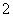 年的本金),那么五年到期時這筆錢連本帶息是否一定夠買一輛(1)中所述降價后的
年的本金),那么五年到期時這筆錢連本帶息是否一定夠買一輛(1)中所述降價后的 型汽車?
型汽車?
解:(1)因為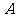 型車
型車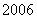 年關稅稅款為
年關稅稅款為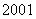 年關稅稅款的
年關稅稅款的 ,故所減少了的關稅稅款為
,故所減少了的關稅稅款為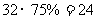 (萬元)。所以,
(萬元)。所以,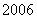 年
年 型車的價格為
型車的價格為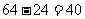 (萬元)。
(萬元)。
因為在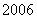 年
年 型車的價格不高于
型車的價格不高于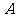 型車價格的
型車價格的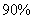 ,所以有:
,所以有: 型車價格
型車價格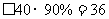 (萬元)。因為
(萬元)。因為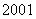 年
年 型車的價格為
型車的價格為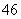 萬元,故五年中至少要降價
萬元,故五年中至少要降價 萬元。所以平均每年至少降價
萬元。所以平均每年至少降價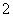 萬元。
萬元。
(2)根據題意,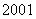 年存入的
年存入的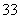 萬元
萬元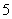 年后到期時連本帶息可得
年后到期時連本帶息可得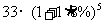 (萬元)。
(萬元)。
因為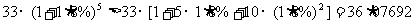 (萬元),所以夠買一輛(1)中所述降價后的
(萬元),所以夠買一輛(1)中所述降價后的 型汽車。
型汽車。
17. 已知等比數列
已知等比數列 的前
的前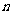 項和為
項和為 ,且
,且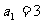 。
。
(1)
求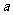 、
、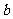 的值及數列
的值及數列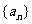 的通項公式;
的通項公式;
(2) 設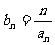 ,求數列
,求數列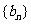 的前
的前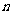 項和
項和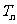 。
。
解:(1) 時,
時,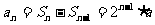 。而
。而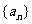 為等比數列,得
為等比數列,得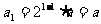 ,
,
又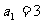 ,得
,得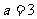 ,從而
,從而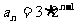 。又
。又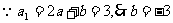 。
。
(2)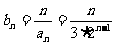 ,
,

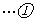


 得
得 ,
,
 。
。
16.已知函數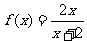 ,當
,當 時,
時,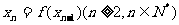 ,求數列
,求數列 的通項公式與
的通項公式與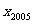 。
。
解:由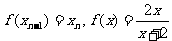 ,得
,得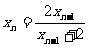 ,即
,即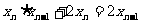 ,
,
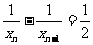 ,所以,數列
,所以,數列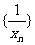 是以首項
是以首項 ,公差為
,公差為 的等差數列。
的等差數列。
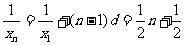 ,
,  ,
,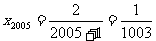 。
。
15.已知數列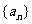 滿足
滿足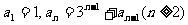 。
。
(1) 求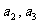 ;
;
(2) 證明: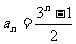 。
。
(1) 解: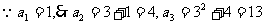 。
。
(2) 證明:由已知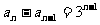 ,故
,故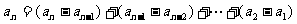
 , 所以證得
, 所以證得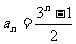 。
。
14.已知函數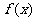 定義在正整數集上,且對于任意的正整數
定義在正整數集上,且對于任意的正整數 ,都有
,都有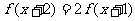
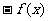 ,且
,且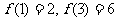 ,則
,則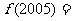 ______________。
______________。
解析:由 知函數
知函數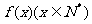 當
當 從小到大依次取值時對應的一系列函數值組成一個等差數列,
從小到大依次取值時對應的一系列函數值組成一個等差數列,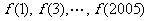 形成一個首項為
形成一個首項為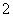 ,公差為
,公差為 的等差數列,
的等差數列,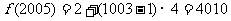 。 答案:
。 答案: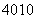
13.對于每一個正整數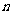 ,拋物線
,拋物線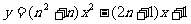 與
與 軸交于
軸交于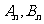 兩點,則
兩點,則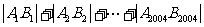 的值為______________。
的值為______________。
解析:令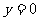 得
得 ,
,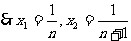 ,
,
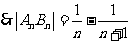

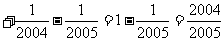 。
答案:
。
答案: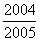
12.若數列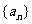 滿足
滿足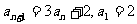 ,則通項公式
,則通項公式 _____________.
_____________.
解析:由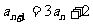 ,得
,得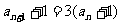 ,這表明數列
,這表明數列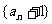 是首項為
是首項為 ,公比
,公比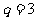 的等比數列,于是有
的等比數列,于是有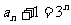 ,即
,即 。
答案:
。
答案:
11.等差數列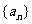 共有
共有 項,其中奇數項之和為
項,其中奇數項之和為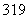 ,偶數項之和為
,偶數項之和為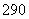 ,則其中間項為______________.
,則其中間項為______________.
解析:依題意,中間項為 ,于是有
,于是有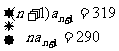 解得
解得 . 答案:
. 答案: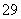
10.三個數 成等比數列,且
成等比數列,且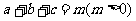 ,則
,則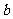 的取值范圍是 ( )
的取值范圍是 ( )
(A) (B)
(B)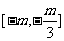 (C)
(C)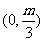 (D)
(D)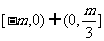
解析:設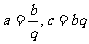 ,則有
,則有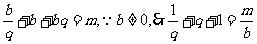 。當
。當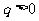 時,
時,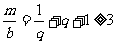 ,而
,而 ,
,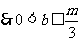 ;當
;當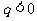 時,
時, ,即
,即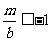 ,而
,而
 ,則
,則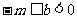 ,故
,故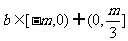 。 答案:D
。 答案:D
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com