
9.若函數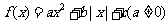 的定義域R分成了四個單調區間,則實數
的定義域R分成了四個單調區間,則實數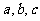 滿足 (
C )
滿足 (
C )
(A)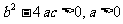 (B)
(B)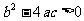 (C)
(C)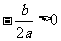 (D)
(D)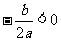
8.
設函數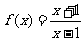 的反函數為
的反函數為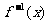 ,若
,若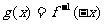 ,則
,則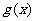 是 ( B
)
是 ( B
)
(A) 上增函數
(B)
上增函數
(B) 上增函數
上增函數
(C)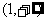 上減函數
(D)
上減函數
(D) 上減函數
上減函數
7.函數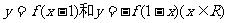 的圖象
( C
)
的圖象
( C
)
(A)關于原點對稱 (B)關于直線x=0對稱
(C)關于點(1,0)對稱 (D)關于直線x=1對稱
6.已知(2,1)在函數f(x)=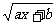 的圖象上,又知f-1
的圖象上,又知f-1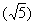 =1,則f(x)等于 ( A )
=1,則f(x)等于 ( A )
(A)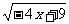 (B)
(B)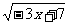 (C)
(C)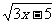 (D)
(D)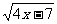
5.在x克a%的鹽水中,加入y克b%的鹽水,濃度變成c%(a,b>0,a≠b),則x與y的函數關系式是 ( B )
(A)y=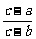 x (B)y=
x (B)y=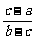 x (C)y=
x (C)y=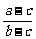 x (D)y=
x (D)y=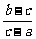 x
x
4.已知函數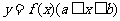 ,集合A={
,集合A={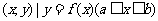 },B={
},B={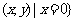 ,
,
則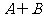 的元素個數為
( C )
的元素個數為
( C )
(A)0 (B)1 (C)0或1 (D)1或2
3.已知函數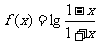 ,若
,若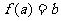 ,則
,則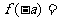 ( B
)
( B
)
(A)
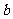 (B)
(B)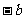 (C)
(C) 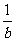 (D)
(D)
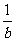
2.“p或q是假命題”是“非p為真命題”的 ( A )
(A)充分而不必要條件 (B)必要而不充分條件
(C)充要條件 (D)既不充分也不必要條件
1.已知集合 則( D )
則( D )
(A)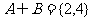 (B)
(B)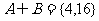 (C)A=B (D)
(C)A=B (D)
6.強化“分類思想”應用。指數函數與對數函數的性質均與其底數是否大于1有關;對于根式的意義及其性質的討論要分清n是奇數還是偶數等。
專題一:集合、映射、簡易邏輯與函數
[經典題例]
例1:給出下列四個命題:
(1)函數y=ax(a>0且a≠1)與函數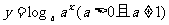 的定義域相同:
的定義域相同:
(2)函數y=x3與y=3x的值域相同;
(3)函數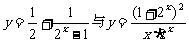 都是奇函數;
都是奇函數;
(4)函數y=(x-1)2與y=2x-1在區間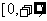 上都是增函數.
上都是增函數.
其中正確命題的序號是 ①③ .(把你認為正確的命題序號都填上)
[簡要評述]
通過這幾種命題的真假判斷,進一步增強學生對比學習意識和數形結合思想
例2:已知f(x)是偶函數,且f(1)=993,g(x)=f(x-1)是奇函數
求f(2005)的值。(993)
[簡要評述]
利用抽象形式推理出函數的重要性質(以4為周期)
例3:關于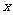 的方程
的方程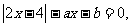
(1) 對于任意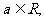 當且僅當
當且僅當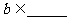 恒有實數解;key:
恒有實數解;key: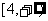
(2) 當且僅當 時恰有兩個實數解;key:
時恰有兩個實數解;key: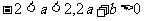
(3) 當且僅當 時由無窮多個實數解;key:
時由無窮多個實數解;key: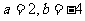 或
或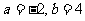
(4) 當且僅當 時無實數解。Key:
時無實數解。Key: 且
且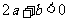
[簡要評述]
通過此題分析增強學生的屬性結合思想意識,培養靈活機動的思維品質。
例4:已知集合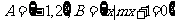 ,若A∪B=A,則符合條件的m的實數值組成的集合
,若A∪B=A,則符合條件的m的實數值組成的集合
是 __________key: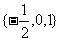
[簡要評述]
在高考應試能力中,,審題是關鍵,通過此題訓練學生思維的嚴謹性。
例5:已知函數 .
.
(1)證明:函數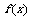 在
在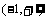 上為增函數;
上為增函數;
(2)用反證法證明方程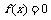 沒有負數根.
沒有負數根.
[思路分析]
證明:設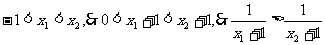
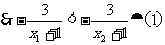
又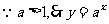 在
在 上是增函數。
上是增函數。 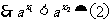 ,
,
由(1)(2)得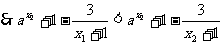 即
即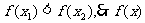
 上是增函數。
上是增函數。
(反證法)設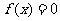 存在負數根,:
存在負數根,: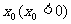 ,則
,則

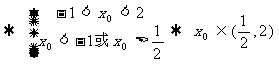 ,又
,又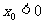 矛盾,所以假設不成立。
矛盾,所以假設不成立。
則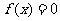 沒有負數根。
沒有負數根。
[簡要評述]通過(1)的證明讓學生在處理函數單調性的證明時,能充分利用幾種基本函數的性質直接處理,同時增強應變能力訓練,通過(2)的證明使學生增強對反證法這種重要數學思想方法的認識。
例6:設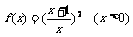 .
.
(1)求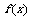 的反函數
的反函數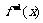 ;
;
(2)若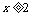 時,不等式
時,不等式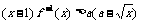 恒成立,試求實數
恒成立,試求實數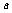 的取值范圍.
的取值范圍.
[思路分析]
(1)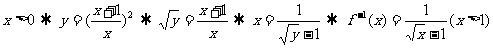
(2)
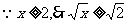 ,顯然
,顯然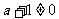
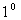 當
當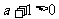 時,
時,
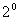 當
當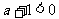 時,
時,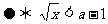
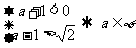 ,綜上所述:
,綜上所述: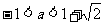
[簡要評述]
該題考查學生對函數與不等式的結合點的認識與處理能力,培養學生的轉化能力及分類討論思想。
例7:高三某班52名學生全部參加綠化美化環境的志愿者行動,這次行動要求完成栽400株花和種200棵樹的任務,據經驗如果栽花每個學生每小時可以栽3株,如果植樹每個學生每小時可以值1棵,現在把這52名學生分成甲乙兩組,甲組只栽花,乙組只植樹,并且同時開始工作,為了在最短時間內完成這項任務,兩組各應安排多少名同學?并論述這種分組的合理性。
解:設甲組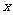 人,乙組
人,乙組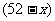 人,
人,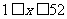 且
且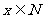 ,
,
據已知,栽花總用時為 小時,植樹總用時為
小時,植樹總用時為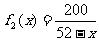 小時,
小時,
這樣完成整個任務的時間,應該是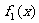 和
和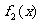 的較大者,
的較大者,
在區間[1,52]上,函數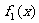 為減函數,
為減函數,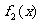 為增函數,為使整體最少,應有|
為增函數,為使整體最少,應有|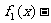
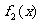 |最小,不妨先解
|最小,不妨先解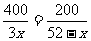 ,得
,得
因為 不是整數,所以要比較兩函數在
不是整數,所以要比較兩函數在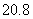 臨近整數的函數值,
臨近整數的函數值,
當 時,|
時,|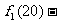
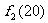 |
|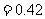 ;
;
當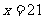 時,|
時,|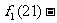
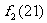 |
|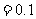 。
。
因此,甲組為21人,乙組為31人,完成任務時間最短。
[簡要評述]
增強應用意識,提高學生學習數學的興趣
例8:已知集合M是滿足下列性質的函數f(x)的全體:存在非零常數T,對任意x∈R,
有f (x+T)=T f (x)成立.
(1)函數f (x)= x 是否屬于集合M?說明理由;
(2)設函數 f (x)= a x (a>0,且a≠1)的圖象與y=x的圖象有公共點,證明:f (x) = a x∈M.
[思路分析] (1)對于非零常數T,f (x+T)=x+T, Tf (x)=Tx.
因為對任意x∈R,x+T= Tx不能恒成立,所以f(x)=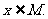
(2)因為函數f (x) = a x(a>0且a≠1)的圖象與函數y=x的圖象有公共點,
所以方程組: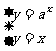 有解,消去y得ax=x,
有解,消去y得ax=x,
顯然x=0不是方程ax=x的解,所以存在非零常數T,使aT=T.
于是對于f (x)=ax有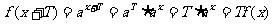 故f (x) = a x∈M.
故f (x) = a x∈M.
[簡要評述]
開放性、探索性問題是當今高考熱點問題,通過此題培養學生科學探索精神。
[熱身沖刺]
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com