日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

122．導數公式你記清了嗎？(理)對復合函數的該如何求導？(①和與差的導數等于導數的和與差；②乘法的求導：前導后不導，后導前不導，中間是正號；③除法的求導：分母平方要記牢，上導下不導，下導上不導，中間是負號)(理) 復合函數的求導問題是個難點，要分清中間變量與復合關系，復合函數求導法則，像鏈條一樣，必須一環一環套下去，而不能丟掉其中的一環. 防止漏掉一部分或漏掉符號造成錯誤.必須正確分析復合函數是由哪些基本函數經過怎樣的順序復合而成的，分清其間的復合關系.

121．導數的概念你理解了嗎？導數有些什么應用。(理)定積分的概念與應用應注意.

① 了解函數單調性和導數的關系；能利用導數研究函數的單調性，會求函數的單調區間，對多項式函數一般不超過三次. ② 了解函數在某點取得極值的必要條件和充分條件；會用導數求函數的極大值、極小值，對多項式函數一般不超過三次；會求閉區間上函數的最大值、最小值，對多項式函數一般不超過三次.

120．(理) 怎樣選擇應用基底(不設直角坐標系)？如何建立直角坐標系及坐標系？

運用空間向量解題，應注意選取適當的基底對相關的向量進行合理的分解。基底的選取應注意以下兩點：一是三個向量不共面；二是這三個向量中兩兩的夾角都可求，一般在四面體、正方體和長方體中，都是以從同一個頂出發的三條棱所在向量作為基底的。

119．(理)利用空間向量解決立體幾何的步驟是什么？運用空間向量的坐標運算解決幾何問題時，一般步驟為：(1)建立適當建立空間直角坐標系；(2)計算出相關點的坐標；(3)寫出向量的坐標，(4)結合公式進行論證、計算；(5)轉化為幾何結論。在建立空間直角坐標系時，必須要牢牢抓住相交于同一點的兩兩垂直的三條直線，要在題目中所給出的垂直關系(如線線垂直、線面垂直與面面垂直等)，同時要注意所建立的直角坐標系必須是右手直角坐標系，在此坐標系下，點的坐標的寫出，可根據圖中有關線段的長度，也可以根據向量的運算。

118．利用空間向量的坐標運算可將立體幾何中有關平行、垂直、夾角、距離等問題轉化為向量的坐標運算，如(1)判斷線線平行或諸點共線，可以轉化為證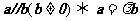；(2)證明線線垂直，轉化為證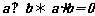，若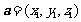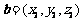，，則轉化為計算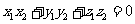；(3)在計算異面直線所成的角(或線面角、二面角)時，轉化為求向量的夾角，利用公式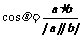；(4)在立體幾何中求線段的長度問題時，轉化為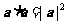，或利用空間兩點間的距離公式。

117．若A(x₁,y₁), B(x₂,y₂)是二次曲線C：F(x,y)=0的弦的兩個端點，則F(x₁,y₁)=0 且F(x₂,y₂)=0。涉及弦的中點和斜率時，常用點差法作F(x₁,y₁)-F(x₂,y₂)=0求得弦AB的中點坐標與弦AB的斜率的關系。

116．過拋物線y²=2px(p>0)焦點的弦交拋物線于A(x₁,y₁),B(x₂,y₂)，則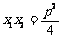，，焦半徑公式|AB|=x₁+x₂+p。

115．通徑是拋物線的所有焦點弦中最短的弦。

114．在用圓錐曲線與直線聯立求解時，消元后得到的方程中要注意：二次項的系數是否為零？判別式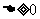的限制．(求交點，弦長，中點，斜率，對稱，存在性問題都在下進行)。

113．在利用圓錐曲線統一定義解題時，你是否注意到定義中的定比的分子分母的順序？