日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

函數單調性是指函數在給定的定義域區間上函數自變量增加時，函數值隨著增減的情況，所以討論函數單調性必須在給定的定義域區間上進行。如：

例4：指出函數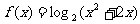的單調區間．

　 解：先求定義域：

　　　 ∵ 　　　∴

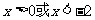
　　　 ∴ 函數定義域為．

　　 令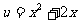，知在上時，u為減函數，

　　　　　　　　　　 在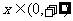上時， u為增函數。

　　 又∵．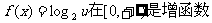

　　　 ∴函數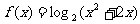在上是減函數，在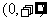上是增函數。

即函數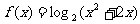的單調遞增區間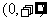，單調遞減區間是。

如果在做題時，沒有在定義域的兩個區間上分別考慮函數的單調性，就說明學生對函數單調性的概念一知半解，沒有理解，在做練習或作業時，只是對題型，套公式，而不去領會解題方法的實質，也說明學生的思維缺乏深刻性。

函數的值域是該函數全體函數值的集合，當定義域和對應法則確定，函數值也隨之而定。因此在求函數值域時，應注意函數定義域。如：

例3：求函數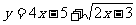的值域．

　 錯解：令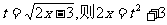

　　　　 ∴

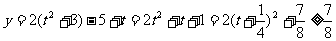
　　　　 故所求的函數值域是．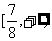

　 剖析：經換元后，應有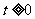，而函數在[0,+∞)上是增函數，

　　　　 所以當t=0時，y_min=1．

　　　　 故所求的函數值域是[1, +∞)．

以上例子說明，變量的允許值范圍是何等的重要，若能發現變量隱含的取值范圍，精細地檢查解題思維的過程，就可以避免以上錯誤結果的產生。也就是說，學生若能在解好題目后，檢驗已經得到的結果，善于找出和改正自己的錯誤，善于精細地檢查思維過程，便體現出良好的思維批判性。

函數的最值是指函數在給定的定義域區間上能否取到最大(小)值的問題。如果不注意定義域，將會導致最值的錯誤。如：

例2：求函數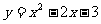在[－2，5]上的最值．

　 解：∵

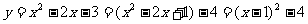
　　　 ∴ 當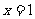時，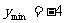

初看結論，本題似乎沒有最大值，只有最小值。產生這種錯誤的根源在于學生是按照求二次函數最值的思路，而沒有注意到已知條件發生變化。這是思維呆板性的一種表現，也說明學生思維缺乏靈活性。

其實以上結論只是對二次函數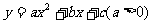在R上適用，而在指定的定義域區間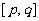上，它的最值應分如下情況：

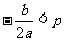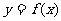　⑴ 當時，在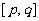上單調遞增函數；

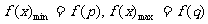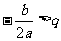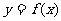　⑵ 當時，在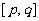上單調遞減函數；

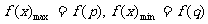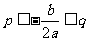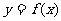　⑶ 當時，在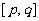上最值情況是：

　 ，

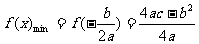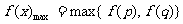　 ．即最大值是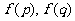中最大的一個值。

故本題還要繼續做下去：

　 ∵

　 ∴

　　　 ∴

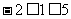
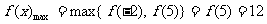
　 ∴ 函數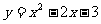在[－2，5]上的最小值是－ 4，最大值是12．　

這個例子說明，在函數定義域受到限制時，若能注意定義域的取值范圍對函數最值的影響，并在解題過程中加以注意，便體現出學生思維的靈活性。

函數關系式包括定義域和對應法則，所以在求函數的關系式時必須要考慮所求函數關系式的定義域，否則所求函數關系式可能是錯誤。如：

例1：某單位計劃建筑一矩形圍墻，現有材料可筑墻的總長度為100m，求矩形的面積S與矩形長x的函數關系式？

　解：設矩形的長為x米，則寬為(50－x)米，由題意得：

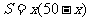
　　 故函數關系式為：．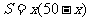

如果解題到此為止，則本題的函數關系式還欠完整，缺少自變量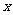的范圍。也就說學生的解題思路不夠嚴密。因為當自變量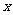取負數或不小于50的數時，S的值是負數，即矩形的面積為負數，這與實際問題相矛盾，所以還應補上自變量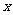的范圍：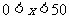

　　 即：函數關系式為： ()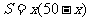

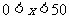這個例子說明，在用函數方法解決實際問題時，必須要注意到函數定義域的取值范圍對實際問題的影響。若考慮不到這一點，就體現出學生思維缺乏嚴密性。若注意到定義域的變化，就說明學生的解題思維過程體現出較好思維的嚴密性。

158．保持良好的心態，是正常發揮、高考取勝的關鍵！

157．涂答題卡時一定要注意，涂完后別忘了仔細檢查(如姓名、準考證號、各題的答案是否對號)

156．上考場前應先檢查是否將工具、準考證全部帶齊。

155．由于高考采取電腦閱卷，所以一定要努力使字跡工整，卷面整潔.并使用0.5mm黑色簽字筆作答.切記在規定區域答題。

154．求軌跡方程的常用方法有：直接法、待定系數法、定義法、轉移法(相關點法)、參數法等。

153.(理)證明不等式常見的方法有幾種?

分析法,綜合法,反證法,放縮法,數學歸納法等.