日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

18、解：(I)(綜合法)連接AC、BD交于菱形的中心O，過O作OGAF，

G為垂足。連接BG、DG。由BDAC，BDCF得BD平面ACF，故BDAF。

于是AF平面BGD，所以BGAF，DGAF，BGD為二面角B－AF－D 的平面角。

由， ，得，

由，得

(向量法)以A為坐標原點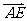，、、方向分別為x軸、y軸、z軸的正方向建立空間直角坐標系(如圖)

設平面ABF的法向量，則由得

令，得，

同理，可求得平面ADF的法向量。 　　　　

由知，平面ABF與平面ADF垂直，

二面角B-AF-D的大小等于。

(II)連EB、EC、ED，設直線AF與直線CE相交于點H，則四棱錐E-ABCD與四棱錐F-ABCD的公共部分為四棱錐H-ABCD。

過H作HP⊥平面ABCD，P為垂足。

因為EA⊥平面ABCD，FC⊥平面ABCD，，所以平面ACFE⊥平面ABCD，從而

由得。

又因為

故四棱錐H-ABCD的體積 　 　　　

17、解：隨機變量X的分布列是

X	1	2	3
P

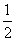X的均值為 　 　　　

附：X的分布列的一種求法

共有如下6種不同的可能情形，每種情形發生的概率都是：

①	②	③	④	⑤	⑥
A-B-C-D	A-B-C └D	A-B-C └D	A-B-D └C	A-C-D └B

在情形①和②之下，A直接感染了一個人；在情形③、④、⑤之下，A直接感染了兩個人；在情形⑥之下，A直接感染了三個人。

16、解：(Ⅰ)由，且，∴，∴，

∴，又，∴

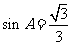
(Ⅱ)如圖，由正弦定理得

∴，又

∴

15、[解析]①④⑤

14、[解析]設

，即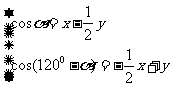

∴

63、127，故輸出的結果是127。

13、[解析] 由程序框圖知，循環體被執行后的值依次為3、7、15、31、

12、[解析] 直線的普通方程為，曲線的普通方程

∴

11、[解析]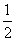　

10、[解析] 如圖，甲從這6個點中任意選兩個點連成直線，乙也從這

6個點中任意選兩個點連成直線，共有

種不同取法，其中所得的兩條直線相互平行但不重合有

共12對，所以所求概率為，選D