
3、[解析]對于
2、[解析]對于“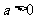 且
且 ”可以推出“
”可以推出“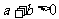 且
且 ”,反之也是成立的
”,反之也是成立的
1-10 BCDBC ACDCC
1、[解析] 對于 ,因此
,因此
 .
.
(18)(本題滿分14分)在 ABC中,角A、B、C所對應的邊分別為a、b、c,且滿足
ABC中,角A、B、C所對應的邊分別為a、b、c,且滿足 =
= ,
,


 =3.
=3.
(Ⅰ)求 的面積;
的面積; 

(Ⅱ)若b+c=6,求a的值。
(19)(本題滿分14分)在1,2,3…,9,這9個自然數中,任取3個數.
(Ⅰ)求這3個數中,恰有一個是偶數的概率; 

(Ⅱ)記ξ為這三個數中兩數相鄰的組數,(例如:若取出的數1、2、3,則有兩組相鄰的數1、2和2、3,此時ξ的值是2)。求隨機變量ξ的分布列及其數學期望Eξ.
(20)(本題滿分15分)如圖,平面 ⊥平面
⊥平面 ,
, 是以
是以 為斜邊的等腰直角三角形。
為斜邊的等腰直角三角形。 分別為
分別為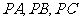 的中點,
的中點, 。
。
(I) 設 是
是 的中點,證明:
的中點,證明: 平面
平面 ;
; 

(II)證明:在 內存在一點
內存在一點 ,使
,使 ⊥平面
⊥平面 ,并求點
,并求點 到
到 ,
, 的距離。
的距離。
(21)(本題滿分15分)已知橢圓 :
: (
( )的右頂點
)的右頂點 (1,0),過
(1,0),過 的焦點且垂直長軸的弦長為1。
的焦點且垂直長軸的弦長為1。 

(I) 求橢圓 的方程;
的方程;
(II) 設點 在拋物線
在拋物線 :
: 上,
上, 在點P處的切線與
在點P處的切線與 交于點
交于點 ,
, 。當線段AP的中點與MN的中點的橫坐標相等時,求
。當線段AP的中點與MN的中點的橫坐標相等時,求 的最小值。
的最小值。
(22)(本題滿分14分)已知函數 ,
, ,其中
,其中 。
。
(I) 設函數 。若
。若


(II)設函數 是否存在
是否存在 ,對任意給定的非零實數
,對任意給定的非零實數 ,存在惟一的非零實數
,存在惟一的非零實數 (
( ),使得
),使得 ?若存在,求
?若存在,求 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
2009年普通高等學校招生全國統一考試(浙江卷)
數 學(理科)
(11)設等比數列 的公比
的公比 ,前n項和為
,前n項和為 ,
,
則 _____________.
_____________.


(12)若某幾何體的三視圖(單元:cm)如圖所示,則
此幾何體的體積是________ .
.
(13)若實數x,y滿足不等式組
的最小值是__________.
(14)某地區居民生活用電分為高峰和低谷兩個時間段進行分時計價,該地區的電網銷售電價表如下:
|
高峰時間段用電價格表 |
|
低谷時間段用電價格表 |
||
|
高峰月用電量 (單位:千瓦時) |
高峰電價 (單位:元/千瓦時) |
|
低谷月用電量 (單位:千瓦時) |
低谷電價 (單位:元/千瓦時) |
|
50及以下的部分 |
0.568 |
|
50及以下的部分 |
0.288 |
|
超過50至200的部分 |
0.598 |
|
超過50至200的部分 |
0.318 |
|
超過200的部分 |
0.668 |
|
超過200的部分 |
0.388 |
若某家庭5月份的高峰時間用電量為200千瓦時,低谷時間段用電量為100千瓦時,則按這種計費方式該家庭本月應付的電費為________元(用數字作答)。
觀察下列等式:
 ,
,
 ,
,
 ,
,
 ,
,
……
由以上等式推測到一個一般的結論:
對于n∈ ,
, _________.
_________. 

(16)甲、乙、丙三人站到共有7級的臺階上,若每級臺階最多站2人,同一級臺階上的人不區分站的位置,則不同的站法種數是________(用數字作答)
(17)如圖,在長方形ABCD中,AB=2,BC=1,E為DC的中點,F為線段EC(端點除外)上一動點,現將 AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD內過點D作DK⊥AB,K為垂足,設AK=t,則t的取值范圍是_______.
AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD內過點D作DK⊥AB,K為垂足,設AK=t,則t的取值范圍是_______.

(1)
設U=R,
(A)

(B) (C)
(C) (D)
(D)
(2)已知a、b是實數,則“a>0,b>0”是a+b>0且ab>0的
(A)充分而不必要條件 (B)必要而不充分條件
(C)充分必要條件 (D)既不充分也不必要條件
(3)設z=1+i(i是虛數單位),則

 (A)-1-i (B)-1+ i (C)1- i (D)1+i
(A)-1-i (B)-1+ i (C)1- i (D)1+i
(4)在二項式 的展開式中,含x4的項的系數是
的展開式中,含x4的項的系數是
(A)-10 (B)10
(C)-5 (D)5
(5)在三棱柱ABC-A1B1C1中,各棱長相等,側棱垂直于底面,點D式側面BB1C1C的中心,則AD與平面BB1C1C所成角的大小是
(A)300 (B)450
(C)600 (D)900
(6)某程序框圖如圖所示,該程序運行后輸出的k的值是
(A)4 (B)5 (C)6 (D)7


(7)設向量a,b滿足︱a︱=3,︱b︱=4, =0.以a,b,a-b的模為邊長構成三角形,則它的邊與半徑為1的圓的公共點個數最多為
=0.以a,b,a-b的模為邊長構成三角形,則它的邊與半徑為1的圓的公共點個數最多為
(A)3 (B)4 (C)5 (D)6
(8)已知a是實數,則函數f(x)=1+asinax的圖像不可能是

(9)過雙曲線 (a>0,b>0)的右頂點A作斜率為-1的直線,該直線與雙曲線的兩條漸近線的交點分別為B,C.若
(a>0,b>0)的右頂點A作斜率為-1的直線,該直線與雙曲線的兩條漸近線的交點分別為B,C.若 =
=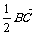 ,則雙曲線的離心率是
,則雙曲線的離心率是 

(A) (B)
(B) (C)
(C)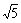 (D)
(D)
(10)對于正實數 ,記M
,記M 為滿足下述條件的函數f(x)構成的集合:
為滿足下述條件的函數f(x)構成的集合: 且
且 >
> ,有-
,有- (
( -
- )<f(
)<f( )-f(
)-f( )<
)< (
( -
- ).下列結論正確的是
).下列結論正確的是
(A)若
(B)
(C)


(D) >
>
2009年普通高等學校招生全國統一考試
數學(理科)
非選擇題部分(共100分)
22.(本題滿分15分)已知拋物線C:x =2py(p>0)上一點A(m,4)到其焦點的距離為
=2py(p>0)上一點A(m,4)到其焦點的距離為 .
.
 (I)求p于m的值;
(I)求p于m的值;
(Ⅱ)設拋物線C上一點p的橫坐標為t(t>0),過p的直線交C于另一點Q,交x軸于M點,過點Q作PQ的垂線交C于另一點N.若MN是C的切線,求t的最小值;
21.(本題滿分15分)已知函數f(x)=x +(1-a) x
+(1-a) x -a(a+2)x+b(a,b
-a(a+2)x+b(a,b R).
R).
(I)若函數f(x)的圖像過原點,且在原點處的切線斜率是-3,求a,b的值;
(Ⅱ)若函數f(x)在區間(-1,1)上不單調,求a的取值范圍. 

20.(本題滿分14分)設 為數列
為數列 的前n項和,
的前n項和,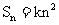 +n,n
+n,n N
N ,其中k是常數.
,其中k是常數.
(I)求 及
及 ;
;
(Ⅱ)若對于任意的m N
N ,a
,a ,a
,a ,a
,a 成等比數列,求k的值.
成等比數列,求k的值.
19.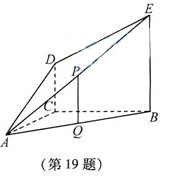 (本題滿分14分)如圖,DC
(本題滿分14分)如圖,DC 平面ABC,EB∥DC,AC=BC=EB=2DC=2,
平面ABC,EB∥DC,AC=BC=EB=2DC=2, ACB=120°,P,Q分別為AE,AB的中點.
ACB=120°,P,Q分別為AE,AB的中點.
(Ⅰ)證明:PQ∥平面ACD;
(Ⅱ)求AD與平面ABE所成角的正弦值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com