
7. 定義在R上的函數f(x)滿足f(x)= 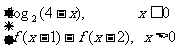 ,則f(3)的值為( B )
,則f(3)的值為( B )
A.-1
B. -2
C.1
D. 2. 

6. 函數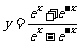 的圖像大致為( A ).
的圖像大致為( A ).


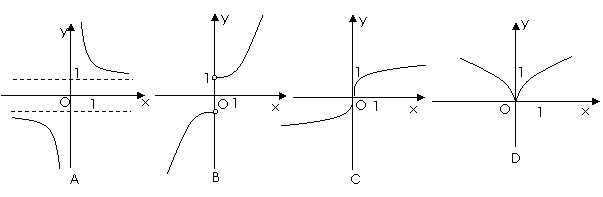
5.在R上定義運算⊙:  ⊙
⊙ ,則滿足
,則滿足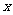 ⊙
⊙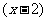 <0的實數
<0的實數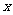 的取值范圍為( B ).
的取值范圍為( B ).
 A.(0,2)
B.(-2,1) C.
A.(0,2)
B.(-2,1) C.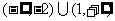 D.(-1,2)
D.(-1,2) 

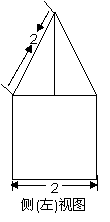
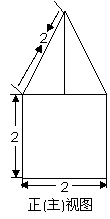
4. 一空間幾何體的三視圖如圖所示,則該幾何體的體積為( C ).
A.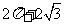 B.
B. 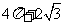 C.
C.
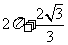 D.
D.
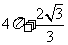
3.將函數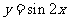 的圖象向左平移
的圖象向左平移 個單位, 再向上平移1個單位,所得圖象的函數解析式是( A).
個單位, 再向上平移1個單位,所得圖象的函數解析式是( A).


A. 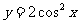 B.
B. 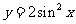 C.
C.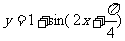 D.
D. 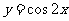
[命題立意]:本題考查三角函數的圖象的平移和利用誘導公式及二倍角公式進行化簡解析式的基本知識和基本技能,學會公式的變形.
2.復數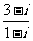 等于(C ).
等于(C ).
A. B.
B.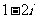 C.
C.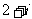 D.
D.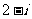
1.集合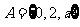 ,
,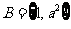 ,若
,若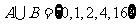 ,則
,則 的值為( D )
的值為( D )
A.0 B.1 C.2 D.4
21、解:(I)已知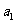 是奇數,假設
是奇數,假設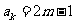 是奇數,其中
是奇數,其中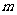 為正整數,
為正整數,
則由遞推關系得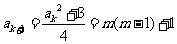 是奇數。
是奇數。 

根據數學歸納法,對任何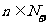 ,
,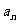 都是奇數。
都是奇數。
(II)(方法一)由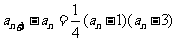 知,
知,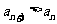 當且僅當
當且僅當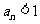 或
或 。
。
另一方面,若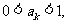 則
則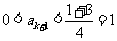 ;若
;若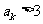 ,則
,則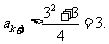
根據數學歸納法,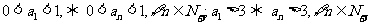
綜合所述,對一切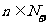 都有
都有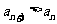 的充要條件是
的充要條件是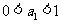 或
或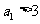 。
。
(方法二)由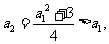 得
得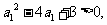 于是
于是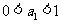 或
或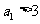 。
。
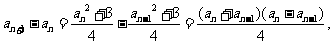


因為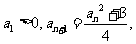 所以所有的
所以所有的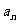 均大于0,因此
均大于0,因此 與
與 同號。
同號。
根據數學歸納法, ,
, 與
與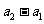 同號。
同號。
因此,對一切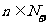 都有
都有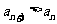 的充要條件是
的充要條件是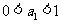 或
或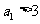 。
。


20、解:本小題主要考查直線和橢圓的標準方程和參數方程,直線和曲線的幾何性質,等比數列等基礎知識。考查綜合運用知識分析問題、解決問題的能力。本小題滿分13分。
解:(I)(方法一)由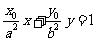 得
得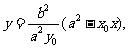 代入橢圓
代入橢圓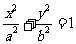 ,
,
得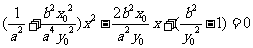 .
.
將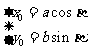 代入上式,得
代入上式,得 從而
從而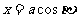
因此,方程組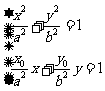 有唯一解
有唯一解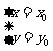 ,即直線
,即直線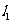 與橢圓有唯一交點P.
與橢圓有唯一交點P. 

(方法二)顯然P是橢圓與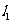 的交點,若Q
的交點,若Q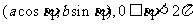 是橢圓與
是橢圓與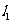 的交點,代入
的交點,代入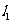 的方程
的方程 ,得
,得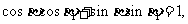
即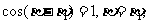 故P與Q重合。
故P與Q重合。
(方法三)在第一象限內,由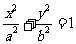 可得
可得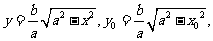
橢圓在點P處的切線斜率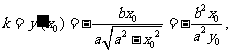
切線方程為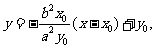 即
即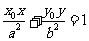 。
。
因此,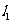 就是橢圓在點P處的切線。
就是橢圓在點P處的切線。
根據橢圓切線的性質,P是橢圓與直線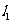 的唯一交點。
的唯一交點。
(II)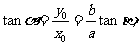
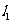 的斜率為
的斜率為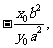
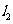 的斜率為
的斜率為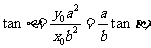
由此得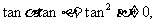
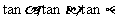 構成等比數列。
構成等比數列。
19、解: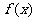 的定義域是(0,+
的定義域是(0,+ ),
),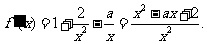
設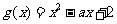 ,二次方程
,二次方程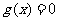 的判別式
的判別式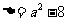 .
.
①
當 ,即
,即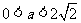 時,對一切
時,對一切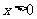 都有
都有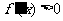 ,此時
,此時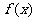 在
在 上是增函數。
上是增函數。
②
當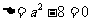 ,即
,即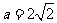 時,僅對
時,僅對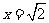 有
有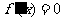 ,對其余的
,對其余的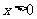 都有
都有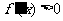 ,此時
,此時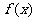 在
在 上也是增函數。
上也是增函數。
③
當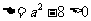 ,即
,即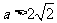 時,
時, 

方程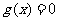 有兩個不同的實根
有兩個不同的實根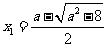 ,
, ,
, .
.
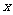 |
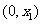 |
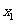 |
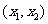 |
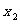 |
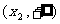 |
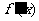 |
+ |
0 |
_ |
0 |
+ |
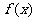 |
單調遞增 |
極大 |
單調遞減 |
極小 |
單調遞增 |
此時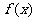 在
在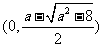 上單調遞增, 在
上單調遞增, 在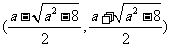 是上單調遞減, 在
是上單調遞減, 在 上單調遞增.
上單調遞增.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com