
5.已知等比數列 的公比為正數,且
的公比為正數,且 ,
,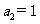 ,則
,則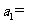
A.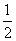 B.
B. C.
C.  D.
D.
4.若函數 是函數
是函數 的反函數,且
的反函數,且 ,則
,則
A. B.
B. C.
C.
 D.
D.
3.已知平面向量a =(x,1),b =(-x,x2 ),則向量a+b
A.平行于x軸 B.平行于第一、三象限的角平分線
C.平行于y軸 D.平行于第二、四象限的角平分線
2.下列n的取值中,使in =1(i是虛數單位)的是
A.n=2 B.n=3 C.n=4 D.n=5
1.已知全集U=R,則正確表示集合M={-1,0,1}和N={ }關系的韋恩(Venn)圖是
}關系的韋恩(Venn)圖是

22. (本小題滿分14分)
設 ,在平面直角坐標系中,已知向量
,在平面直角坐標系中,已知向量 ,向量
,向量 ,
,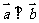 ,動點
,動點 的軌跡為E.
的軌跡為E.
(1)求軌跡E的方程,并說明該方程所表示曲線的形狀;
(2)已知 ,證明:存在圓心在原點的圓,使得該圓的任意一條切線與軌跡E恒有兩個交點A,B,且
,證明:存在圓心在原點的圓,使得該圓的任意一條切線與軌跡E恒有兩個交點A,B,且 (O為坐標原點),并求出該圓的方程;
(O為坐標原點),并求出該圓的方程;
(3)已知 ,設直線
,設直線 與圓C:
與圓C: (1<R<2)相切于A1,且
(1<R<2)相切于A1,且 與軌跡E只有一個公共點B1,當R為何值時,|A1B1|取得最大值?并求最大值.
與軌跡E只有一個公共點B1,當R為何值時,|A1B1|取得最大值?并求最大值.
解:(1)因為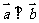 ,
, ,
, ,
,
所以 , 即
, 即 .
.
當m=0時,方程表示兩直線,方程為 ;
;
當 時, 方程表示的是圓
時, 方程表示的是圓
當 且
且 時,方程表示的是橢圓;
時,方程表示的是橢圓;
當 時,方程表示的是雙曲線.
時,方程表示的是雙曲線.
(2).當 時, 軌跡E的方程為
時, 軌跡E的方程為 ,設圓心在原點的圓的一條切線為
,設圓心在原點的圓的一條切線為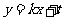 ,解方程組
,解方程組 得
得 ,即
,即 ,
,
要使切線與軌跡E恒有兩個交點A,B,
則使△= ,
,
即 ,即
,即 , 且
, 且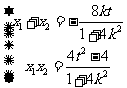
 ,
,
要使 , 需使
, 需使 ,即
,即 ,
,
所以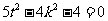 , 即
, 即 且
且 , 即
, 即 恒成立.
恒成立.
所以又因為直線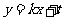 為圓心在原點的圓的一條切線,
為圓心在原點的圓的一條切線,
所以圓的半徑為 ,
, , 所求的圓為
, 所求的圓為 .
.
當切線的斜率不存在時,切線為 ,與
,與 交于點
交于點 或
或 也滿足
也滿足 .
.
綜上, 存在圓心在原點的圓 ,使得該圓的任意一條切線與橢圓E恒有兩個交點A,B,且
,使得該圓的任意一條切線與橢圓E恒有兩個交點A,B,且 .
.
(3)當 時,軌跡E的方程為
時,軌跡E的方程為 ,設直線
,設直線 的方程為
的方程為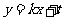 ,因為直線
,因為直線 與圓C:
與圓C: (1<R<2)相切于A1, 由(2)知
(1<R<2)相切于A1, 由(2)知 , 即
, 即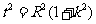 ①,
①,
因為 與軌跡E只有一個公共點B1,
與軌跡E只有一個公共點B1,
由(2)知 得
得 ,
,
即 有唯一解
有唯一解
則△= , 即
, 即 ,
②
,
②
由①②得 , 此時A,B重合為B1(x1,y1)點,
, 此時A,B重合為B1(x1,y1)點,
由 中
中 ,所以,
,所以, ,
,
B1(x1,y1)點在橢圓上,所以 ,所以
,所以 ,
,
在直角三角形OA1B1中, 因為
因為 當且僅當
當且僅當 時取等號,所以
時取等號,所以 ,即
,即
當 時|A1B1|取得最大值,最大值為1.
時|A1B1|取得最大值,最大值為1.
徐洪艷制作
21.(本小題滿分12分)
已知函數 ,其中
,其中


(1) 當 滿足什么條件時,
滿足什么條件時, 取得極值?
取得極值?
(2) 已知 ,且
,且 在區間
在區間 上單調遞增,試用
上單調遞增,試用 表示出
表示出 的取值范圍.
的取值范圍.
解: (1)由已知得 ,令
,令 ,得
,得 ,
,
 要取得極值,方程
要取得極值,方程 必須有解,
必須有解,
所以△ ,即
,即 , 此時方程
, 此時方程 的根為
的根為
 ,
, ,
,
所以


當 時,
時,
|
x |
(-∞,x1) |
x 1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
增函數 |
極大值 |
減函數 |
極小值 |
增函數 |
所以 在x 1,
x2處分別取得極大值和極小值.
在x 1,
x2處分別取得極大值和極小值.
當 時,
時, 

|
x |
(-∞,x2) |
x 2 |
(x2,x1) |
x1 |
(x1,+∞) |
|
f’(x) |
- |
0 |
+ |
0 |
- |
|
f (x) |
減函數 |
極小值 |
增函數 |
極大值 |
減函數 |
所以 在x 1,
x2處分別取得極大值和極小值.
在x 1,
x2處分別取得極大值和極小值.
綜上,當 滿足
滿足 時,
時,  取得極值.
取得極值. 

(2)要使 在區間
在區間 上單調遞增,需使
上單調遞增,需使 在
在 上恒成立.
上恒成立.
即 恒成立, 所以
恒成立, 所以
設 ,
, ,
,
令 得
得 或
或 (舍去),
(舍去), 

當 時,
時, ,當
,當 時
時 ,
, 單調增函數;
單調增函數;
當 時
時 ,
, 單調減函數,
單調減函數,
所以當 時,
時, 取得最大,最大值為
取得最大,最大值為 .
.
所以
當 時,
時, ,此時
,此時 在區間
在區間 恒成立,所以
恒成立,所以 在區間
在區間 上單調遞增,當
上單調遞增,當 時
時 最大,最大值為
最大,最大值為 ,所以
,所以
綜上,當 時,
時,  ; 當
; 當 時,
時, 


20.(本小題滿分12分)
等比數列{ }的前n項和為
}的前n項和為 , 已知對任意的
, 已知對任意的 ,點
,點 ,均在函數
,均在函數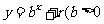 且
且 均為常數)的圖像上.
均為常數)的圖像上. 

(1)求r的值;
(11)當b=2時,記  求數列
求數列 的前
的前 項和
項和
解:因為對任意的 ,點
,點 ,均在函數
,均在函數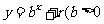 且
且 均為常數)的圖像上.所以得
均為常數)的圖像上.所以得 ,
,
當 時,
時, ,
, 

當 時,
時, ,
,
又因為{ }為等比數列, 所以
}為等比數列, 所以 , 公比為
, 公比為 , 所以
, 所以
(2)當b=2時, ,
, 
則



相減,得


所以
19. (本小題滿分12分)
一汽車廠生產A,B,C三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛):
|
|
轎車A |
轎車B |
轎車C |
|
舒適型 |
100 |
150 |
z |
|
標準型 |
300 |
450 |
600 |
按類型分層抽樣的方法在這個月生產的轎車中抽取50輛,其中有A類轎車10輛.
(1) 求z的值. 

(2) 用分層抽樣的方法在C類轎車中抽取一個容量為5的樣本.將該樣本看成一個總體,從中任取2輛,求至少有1輛舒適型轎車的概率;
(3) 用隨機抽樣的方法從B類舒適型轎車中抽取8輛,經檢測它們的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把這8輛轎車的得分看作一個總體,從中任取一個數,求該數與樣本平均數之差的絕對值不超過0.5的概率.
解: (1).設該廠本月生產轎車為n輛,由題意得,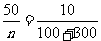 ,所以n=2000. z=2000-100-300-150-450-600=400
,所以n=2000. z=2000-100-300-150-450-600=400
(2) 設所抽樣本中有m輛舒適型轎車,因為用分層抽樣的方法在C類轎車中抽取一個容量為5的樣本,所以 ,解得m=2也就是抽取了2輛舒適型轎車,3輛標準型轎車,分別記作S1,S2;B1,B2,B3,則從中任取2輛的所有基本事件為(S1,
B1), (S1, B2) , (S1, B3)
(S2 ,B1), (S2 ,B2), (S2 ,B3),(
(S1, S2),(B1 ,B2), (B2 ,B3)
,(B1 ,B3)共10個,其中至少有1輛舒適型轎車的基本事件有7個基本事件: (S1, B1),
(S1, B2) , (S1, B3) (S2 ,B1),
(S2 ,B2), (S2 ,B3),( (S1,
S2),所以從中任取2輛,至少有1輛舒適型轎車的概率為
,解得m=2也就是抽取了2輛舒適型轎車,3輛標準型轎車,分別記作S1,S2;B1,B2,B3,則從中任取2輛的所有基本事件為(S1,
B1), (S1, B2) , (S1, B3)
(S2 ,B1), (S2 ,B2), (S2 ,B3),(
(S1, S2),(B1 ,B2), (B2 ,B3)
,(B1 ,B3)共10個,其中至少有1輛舒適型轎車的基本事件有7個基本事件: (S1, B1),
(S1, B2) , (S1, B3) (S2 ,B1),
(S2 ,B2), (S2 ,B3),( (S1,
S2),所以從中任取2輛,至少有1輛舒適型轎車的概率為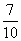 .
.
(3)樣本的平均數為 ,
,
那么與樣本平均數之差的絕對值不超過0.5的數為9.4, 8.6, 9.2, 8.7, 9.3, 9.0這6個數,總的個數為8,所以該數與樣本平均數之差的絕對值不超過0.5的概率為 .
.
18.(本小題滿分12分)
 如圖,在直四棱柱ABCD-A
如圖,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD為等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD為等腰梯形,AB//CD,AB=4, BC=CD=2, AA =2, E、E
=2, E、E 分別是棱AD、AA
分別是棱AD、AA 的中點.
的中點. 

(1) 設F是棱AB的中點,證明:直線EE //平面FCC
//平面FCC ;
;
(2) 證明:平面D1AC⊥平面BB1C1C.
證明:(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中點F1,
中,取A1B1的中點F1,
 連接A1D,C1F1,CF1,因為AB=4, CD=2,且AB//CD,
連接A1D,C1F1,CF1,因為AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD為平行四邊形,所以CF1//A1D,
又因為E、E 分別是棱AD、AA
分別是棱AD、AA 的中點,所以EE1//A1D,
的中點,所以EE1//A1D,
所以CF1//EE1,又因為 平面FCC
平面FCC ,
, 平面FCC
平面FCC ,
,
所以直線EE //平面FCC
//平面FCC .
.
 (2)連接AC,在直棱柱中,CC1⊥平面ABCD,AC
(2)連接AC,在直棱柱中,CC1⊥平面ABCD,AC 平面ABCD,
平面ABCD,
所以CC1⊥AC,因為底面ABCD為等腰梯形,AB=4, BC=2,
F是棱AB的中點,所以CF=CB=BF,△BCF為正三角形,
 ,△ACF為等腰三角形,且
,△ACF為等腰三角形,且
所以AC⊥BC, 又因為BC與CC1都在平面BB1C1C內且交于點C,
所以AC⊥平面BB1C1C,而 平面D1AC,
平面D1AC,
所以平面D1AC⊥平面BB1C1C.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com