
中央集權制度是中國古代基本的政治制度。據此回答1-3題。
1.秦朝中央集權制度的主要特點有( )
①皇權至上 ②三公九卿之間互相配合,互相牽制 ③刺史代表中央監察地方 ④郡守、縣令均由朝廷任命
A.①②④ B.②③④ C.①②③ D.①③④
2.(07年高考全國文綜卷Ⅱ)隋唐實行三省六部制。唐初三省的職能是( )
A.尚書省和中書省決策,門下省執行 B.中書省決策,門下省和尚書省執行
C.門下省決策,中書省和尚書省執行 D.中書省和門下省決策,尚書省執行
3.中央集權與地方分權的斗爭是中國古代政治史上的重要內容。下列屬于加強中央集權的措施有( )
①秦朝皇帝直接任命郡縣長官②隋唐確立和完善三省六部制③北宋任用文臣做地方長官④明朝廢除丞相
A.①⑧ B.②③④ C.①③④ D.①②③④
數學充滿著辯證法,一般性往往寓于特殊性之中。解題時,將一般問題特殊化和將特殊問題一般化是常用的兩種策略。對一些較為抽象或一般規律又無顯露的數學問題,尤其是答案相對唯一的選擇題,可以采用抽象問題具體化,一般問題特殊化的方法來驗證,而無需作費時費力的嚴格推證,從而避免“小題大做”,以降低難度,盡快確定正確答案。
 例6、(2001年全國高考)一間民房的屋頂有如下圖三種不同的蓋法:
例6、(2001年全國高考)一間民房的屋頂有如下圖三種不同的蓋法:
①單向傾斜;②雙向傾斜;③四向傾斜。記三種蓋法屋頂面積分別為P1、P2、P3。若屋頂斜面與水平面所成的角都是α,則( ) (A)P3=P2>P1 (B)P3>P2=P1 (C)P3>P2>P1 (D)P3=P2=P1
分析:由射影面積公式(  )可知:
)可知: 與斜面和水平面所成角
與斜面和水平面所成角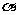 有關,而與斜面內圖形形狀及圖形放置無關。所以可以抓住“所成角都是
有關,而與斜面內圖形形狀及圖形放置無關。所以可以抓住“所成角都是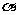 ”及“射影面積(民房面積)不變”,取特值
”及“射影面積(民房面積)不變”,取特值 ,就將三種不同的房蓋均變成平房蓋,而同一間民房的面積全部相同,從而得解。
,就將三種不同的房蓋均變成平房蓋,而同一間民房的面積全部相同,從而得解。
解:令 ,即可知選D。
,即可知選D。
當然,除了上述常用方法外,數學解題中還存在其它的轉化方法,如:在求空間距離問題時,可利用等積法(點線距離常用等面積法,點面距離常用等體積法)將它轉化為解三角形的問題;在求空間角(異面直線所成的角或二面角的平面角)時,可通過平移變換、作輔助線等方法轉化為同一個平面或三角形中;而求函數的值域(或最值),有時也可以根據反函數的性質,通過求該函數的反函數的定義域來得到。……由于本文篇幅有限,這里就不一一舉例。
總而言之,化歸與轉化的思想具有靈活性和多樣性的特點,沒有統一的模式可遵循,需要依據問題本身提供的信息,利用動態思維,去尋找有利于問題解決的變換途徑和方法,所以學習和熟悉化歸與轉化的思想,有意識地運用數學變換的方法,去靈活地解決有關的數學問題,將有利于提高解決數學問題的應變能力和技能、技巧。
對結構較為復雜,量與量之間的關系不甚明了的命題,通過適當的引入新變量(換元),往往可以簡化原有結構,使其轉化為便于研究的形式。常用的換元法有代數代換、三角代換、整體代換等。在應用換元法時要特別注意新變量的取值范圍,即代換的等價性。
例5、(2004年高考廣西理科)解方程:
分析:若令 ,(
,( ),則原方程可轉化為求含絕對值的二次方程的解。
),則原方程可轉化為求含絕對值的二次方程的解。
解:令 ,(
,( ),原方程可化為:
),原方程可化為:
①當 (即
(即 )時,方程可化為:
)時,方程可化為: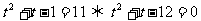
解之得: ,或
,或 (不舍題意,舍去)
(不舍題意,舍去)

②當 (即
(即 )時,方程可化為:
)時,方程可化為:
解之得: 或
或 (均不舍題意,舍去)
(均不舍題意,舍去)
所以,原方程的解為 
函數與方程的思想是求數量關系的主要思想方法。一個數學問題,如能建立描述其數量特征的函數表達式,或列出表示其數量關系的方程式(組)(包括不等式(組)),則一般可使問題得到解答。
例4、已知平行四邊形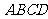 中,點
中,點 的坐標分別為(
的坐標分別為( ,點
,點 在橢圓
在橢圓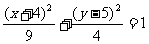 上移動,求點
上移動,求點 的軌跡方程。
的軌跡方程。
分析:因為平行四邊形的對邊平行且相等,所以可以將本題轉化為相等向量的性質來求解。
解:設 的坐標分別為
的坐標分別為
則
 在平行四邊形
在平行四邊形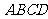 中,
中,


 點
點 在橢圓上,
在橢圓上,
 把
把 點坐標
點坐標 代入橢圓方程中,
代入橢圓方程中,
即得點 的軌跡方程:
的軌跡方程: 
數形結合的思想就是把問題的數量關系和空間形式結合起來加以考察的思想,其實質就是把抽象的數量關系和直觀的圖形結合起來,從而降低原命題的難度,使問題容易得到解決。
例3、如果實數 滿足
滿足 ,那么
,那么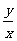 的最大值是( )
的最大值是( )
A. B.
B. C.
C. D.
D.
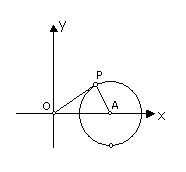 分析:由于方程
分析:由于方程 表示的曲線以
表示的曲線以 為圓心,以
為圓心,以 為半徑的圓(如右圖所示),滿足方程的
為半徑的圓(如右圖所示),滿足方程的 是圓上的點
是圓上的點 ;而
;而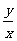 是坐標原點
是坐標原點 與圓上各點連線的斜率,所以題目可轉化為求原點
與圓上各點連線的斜率,所以題目可轉化為求原點 與圓上各點連線的斜率的最大值。結合圖像,易知直線
與圓上各點連線的斜率的最大值。結合圖像,易知直線 與圓
與圓 相切的時候,直線
相切的時候,直線 的斜率
的斜率 就是所求斜率的最大值。
就是所求斜率的最大值。
解:


即所求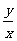 的最大值是
的最大值是 ,故選D。
,故選D。
如果一個命題從正面解決不好入手或比較麻煩,可以從命題的反面入手來解決。如:證明命題的唯一性、無理性,或所給的命題以否定形式出現(如:不存在、不相交等),并伴有“至少”“不都”“都不”“沒有”等指示性詞語時,均可考慮用反證法的思想來實現轉化。反證法是數學解題中逆向思維的直接體現。
例2、已知下列三個方程: ,
, ,
, 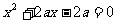 中,至少有一個方程有實根,求實數
中,至少有一個方程有實根,求實數 的取值范圍。
的取值范圍。
分析:此題若采用正面討論,則必須分成“有且只有一個方程有實根”,“有兩個方程有實根”和“三個方程全部有實根”三種不同情況來討論,求解過程將會非常復雜。所以,應采用補集和反證法的思想來求。
解:若方程沒有一個有實根,則有
解之得:
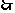 滿足三個方程至少有一個方程有實根的
滿足三個方程至少有一個方程有實根的 的解集是
的解集是 。
。
在數學中,存在許許多多具有等價性的問題,“恒等變形”是解題的最基本的方法,如解方程和不等式的過程本身就是一個等價轉化的過程。
例1、(2003年全國高考)已知 。設
。設 函數
函數 在
在 上單調遞減。
上單調遞減。 不等式
不等式 的解集為
的解集為 。如果
。如果 和
和 有且僅有一個正確,求
有且僅有一個正確,求 的取值范圍。
的取值范圍。
分析:“ 和
和 有且僅有一個正確”等價于“
有且僅有一個正確”等價于“ 正確且
正確且 不正確”或“
不正確”或“ 不正確且
不正確且 正確”,所以應先求出
正確”,所以應先求出 和
和 分別正確時的解集,再用集合間的關系來運算。
分別正確時的解集,再用集合間的關系來運算。
解: 函數
函數 在
在 上單調遞減
上單調遞減
 不等式
不等式 的解集為
的解集為
 函數
函數 在
在 上恒大于1。
上恒大于1。


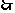 函數
函數 在
在 上的最小值為
上的最小值為 。
。
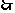 不等式
不等式 的解集為
的解集為
 。
。
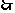 如果
如果 正確且
正確且 不正確,則
不正確,則
如果 不正確且
不正確且 正確,則
正確,則
所以 的取值范圍為
的取值范圍為 。
。
8.(★★★★★)It’s a fine day. Let’s go fishing,________?
A.won’t we B.will we
C.don’t we D.shall we (NMET1990)
7.(★★★★★)She hardly ever speaks to you in English, ________?
A.does she B.doesn’t she
’t she
6.(★★★★★)Don’t smoke in the meeting room,________?
A.do you B.will you
you D.could you (NMET1991)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com