日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

6. 已知8支球隊中有3支弱隊,以抽簽方式將這8支球隊分為A、B兩組,每組4支.求：

(Ⅰ)A、B兩組中有一組恰有兩支弱隊的概率；

(Ⅱ)A組中至少有兩支弱隊的概率.　 (2004年全國卷Ⅱ)

解：(Ⅰ)解法一：三支弱隊在同一組的概率為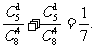

故有一組恰有兩支弱隊的概率為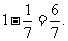

解法二：有一組恰有兩支弱隊的概率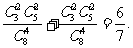

(Ⅱ)解法一：A組中至少有兩支弱隊的概率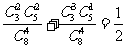

　　　 解法二：A、B兩組有一組至少有兩支弱隊的概率為1，由于對A組和B組來說，至少有兩支弱隊的概率是相同的，所以A組中至少有兩支弱隊的概率為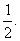

1　 甲、乙二人參加普法知識競賽，共有10個不同的題目，其中選擇題6個，判斷題4個，甲、乙二人依次各抽一題.

(Ⅰ)甲抽到選擇題、乙抽到判斷題的概率是多少？

(Ⅱ)甲、乙二人中至少有一人抽到選擇題的概率是多少？(2000年新課程卷)

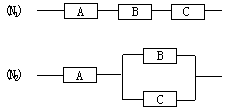
2 如圖,用A、B、C三類不同的元件連接成兩個系統N₁、N₂.當元件A、B、C都正常工作時,系統N₁正常工作；當元件A正常工作且元件B、C至少有一個正常工作時,系統N₂正常工作.已知元件A、B、C正常工作的概率依次為0.80,0.90,0.90.分別求系統N₁、N₂正常工作的概率P₁、P₂.　 (2001年新課程卷)

3　 某單位6個員工借助互聯網開展工作，每個員工上網的概率都是0.5(相互獨立).

(Ⅰ)求至少3人同時上網的概率；

(Ⅱ)至少幾人同時上網的概率小于0.3？(2002年新課程卷)

4　 有三種產品，合格率分別是0.90，0.95和0.95，各抽取一件進行檢驗.

(Ⅰ)求恰有一件不合格的概率；

(Ⅱ)求至少有兩件不合格的概率.(精確到0.001) (2003年新課程卷)

5. 從10位同學(其中6女，4男)中隨機選出3位參加測驗.每位女同學能通過測驗的概率均為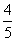，每位男同學能通過測驗的概率均為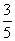.試求：

(Ⅰ)選出的3位同學中，至少有一位男同學的概率；

(Ⅱ)10位同學中的女同學甲和男同學乙同時被選中且通過測驗的概率.

　(2004年全國卷Ⅰ)

解：本小題主要考查組合，概率等基本概念，獨立事件和互斥事件的概率以及運用概率知識

　　 解決實際問題的能力，滿分12分.

　　 解：(Ⅰ)隨機選出的3位同學中，至少有一位男同學的概率為

　　　　　　 1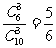－；………………6分

(Ⅱ)甲、乙被選中且能通過測驗的概率為

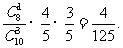　　　　　　 ；………………12分

8．會計算事件在n次獨立重復試驗中恰好發生k次的概率.

Ⅰ、隨機事件的概率　

例1 　某商業銀行為儲戶提供的密碼有0，1，2，…，9中的6個數字組成.

(1)某人隨意按下6個數字，按對自己的儲蓄卡的密碼的概率是多少？

(2)某人忘記了自己儲蓄卡的第6位數字，隨意按下一個數字進行試驗，按對自己的密碼的概率是多少？

解 (1)儲蓄卡上的數字是可以重復的，每一個6位密碼上的每一個數字都有0，1，2，…，9這10種，正確的結果有1種，其概率為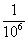，隨意按下6個數字相當于隨意按下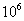個，隨意按下6個數字相當于隨意按下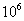個密碼之一，其概率是.

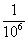(2)以該人記憶自己的儲蓄卡上的密碼在前5個正確的前提下，隨意按下一個數字，等可能性的結果為0，1，2，…，9這10種，正確的結果有1種，其概率為.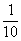

例2 　一個口袋內有m個白球和n個黑球，從中任取3個球，這3個球恰好是2白1黑的概率是多少？(用組合數表示)

解　 設事件I是“從m個白球和n個黑球中任選3個球”，要對應集合I₁，事件A是“從m個白球中任選2個球，從n個黑球中任選一個球”，本題是等可能性事件問題，且Card(I₁)= 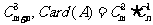，于是P(A)=.

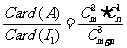Ⅱ、互斥事件有一個發生的概率

例3在20件產品中有15件正品，5件次品，從中任取3件，求：

(1)恰有1件次品的概率；(2)至少有1件次品的概率.

解 (1)從20件產品中任取3件的取法有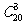，其中恰有1件次品的取法為.

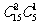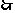恰有一件次品的概率P=.

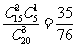(2)法一 從20件產品中任取3件，其中恰有1件次品為事件A₁,恰有2件次品為事件A₂，3件全是次品為事件A₃,則它們的概率

P(A₁)= =,,,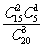

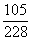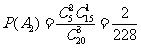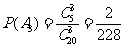而事件A₁、A₂、A₃彼此互斥，因此3件中至少有1件次品的概率

P(A₁+A₂+A₃)=P(A₁)+P(A₂)+P(A₃)= .

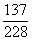法二 記從20件產品中任取3件，3件全是正品為事件A，那么任取3件，至少有1件次品為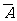，根據對立事件的概率加法公式P()=

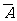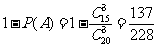
例4 1副撲克牌有紅桃、黑桃、梅花、方塊4種花色，每種13張，共52張，從1副洗好的牌中任取4張，求4張中至少有3張黑桃的概率.

解　 從52張牌中任取4張，有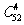種取法.“4張中至少有3張黑桃”，可分為“恰有3張黑桃”和“4張全是黑桃”，共有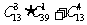種取法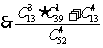

注　 研究至少情況時，分類要清楚.

Ⅲ、相互獨立事件同時發生的概率

例5 獵人在距離100米處射擊一野兔，其命中率為0.5，如果第一次射擊未中，則獵人進行第二次射擊，但距離150米. 如果第二次射擊又未中，則獵人進行第三次射擊，并且在發射瞬間距離為200米. 已知獵人的命中概率與距離的平方成反比，求獵人命中野兔的概率.

解　 記三次射擊依次為事件A，B，C，其中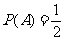,由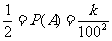，求得k=5000.

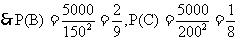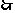,命中野兔的概率為

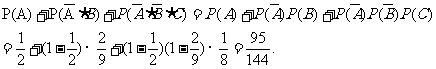
例6　 要制造一種機器零件，甲機床廢品率為0.05，而乙機床廢品率為0.1，而它們的生產是獨立的，從它們制造的產品中，分別任意抽取一件，求：

(1)其中至少有一件廢品的概率； (2)其中至多有一件廢品的概率.

解： 設事件A為“從甲機床抽得的一件是廢品”；B為“從乙機床抽得的一件是廢品”.

則P(A)=0.05,　 P(B)=0.1,

(1)至少有一件廢品的概率

(2)至多有一件廢品的概率

Ⅳ、概率內容的新概念較多，本課時就學生易犯錯誤作如下歸納總結：

類型一　 “非等可能”與“等可能”混同

例1　 擲兩枚骰子，求所得的點數之和為6的概率．

錯解　 擲兩枚骰子出現的點數之和2，3，4，…，12共11種基本事件，所以概率為P=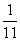

剖析　 以上11種基本事件不是等可能的，如點數和2只有(1，1)，而點數之和為6有(1，5)、(2，4)、(3，3)、(4，2)、(5，1)共5種．事實上，擲兩枚骰子共有36種基本事件，且是等可能的，所以“所得點數之和為6”的概率為P=．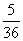

類型二　 “互斥”與“對立”混同

例2　 把紅、黑、白、藍4張紙牌隨機地分給甲、乙、丙、丁4個人，每個人分得1張，事件“甲分得紅牌”與“乙分得紅牌”是(　　　 )

　 　　A．對立事件　 　B．不可能事件 　C．互斥但不對立事件 　　D．以上均不對

錯解　 A

剖析　 本題錯誤的原因在于把“互斥”與“對立”混同，二者的聯系與區別主要體現在　 ：

　　 　(1)兩事件對立，必定互斥，但互斥未必對立；(2)互斥概念適用于多個事件，但對立概念只適用于兩個事件；(3)兩個事件互斥只表明這兩個事件不能同時發生，即至多只能發生其中一個，但可以都不發生；而兩事件對立則表示它們有且僅有一個發生．

　　 　事件“甲分得紅牌”與“乙分得紅牌”是不能同時發生的兩個事件，這兩個事件可能恰有一個發生，一個不發生，可能兩個都不發生，所以應選C．

類型三　 “互斥”與“獨立”混同

例3　 甲投籃命中率為O．8，乙投籃命中率為0.7，每人投3次，兩人恰好都命中2次的概率是多少?

錯解　 設“甲恰好投中兩次”為事件A，“乙恰好投中兩次”為事件B，則兩人都恰好投中兩次為事件A+B，P(A+B)=P(A)+P(B)：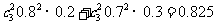

剖析　 本題錯誤的原因是把相互獨立同時發生的事件當成互斥事件來考慮，將兩人都恰好投中2次理解為“甲恰好投中兩次”與“乙恰好投中兩次”的和．互斥事件是指兩個事件不可能同時發生；兩事件相互獨立是指一個事件的發生與否對另一個事件發生與否沒有影響，它們雖然都描繪了兩個事件間的關系，但所描繪的關系是根本不同．

解：　 設“甲恰好投中兩次”為事件A，“乙恰好投中兩次”為事件B，且A，B相互獨立，

則兩人都恰好投中兩次為事件A·B，于是P(A·B)=P(A)×P(B)= 0.169

7．了解互斥事件、相互獨立事件的意義，會用互斥事件的概率加法公式與相互獨立事件的概率乘法公式計算一些事件的概率.

6．了解等可能性事件的概率的意義，會用排列組合的基本公式計算一些等可能性事件的概率.

5．了解隨機事件的發生存在著規律性和隨機事件概率的意義.

4．掌握二項式定理和二項展開式的性質，并能用它們計算和證明一些簡單的問題.

3．理解組合的意義，掌握組合數計算公式和組合數的性質，并能用它們解決一些簡單的應用問題.

2．理解排列的意義，掌握排列數計算公式，并能用它解決一些簡單的應用問題.

1．掌握分類計數原理與分步計數原理，并能用它們分析和解決一些簡單的應用問題.