日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

1求證：

證明：左邊＝＝右邊

或：右邊＝tan(x－)

＝＝左邊

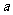2若0＜α＜β＜，sinα+cosα＝，sinβ+cosβ＝b，則

Aab＜1　　　　　　　　 Ba＞b

Ca＜b　　　　　　　　 　Dab＞2

解：sinα+cosα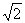＝sin(α+)＝a

sinβ+cosβ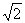＝sin(β+)＝b

又∵0＜α＜β＜

∴0＜α+＜β+＜

∴sin(α+)＜sin(β+)

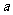∴＜b

答案：C

1 在△ABC中，ÐC>90°，則tanAtanB與1的關系適合………………(B)

(A) tanAtanB>1　　 (B) tanAtanB>1　　 (C) tanAtanB =1　　 (D)不確定

解：在△ABC中　 ∵ÐC>90°　 ∴A, B為銳角　 即tanA>0, tanB>0

又tanC<0　 于是：tanC = -tan(A+B) = <0

∴1 - tanAtanB>0　 即：tanAtanB<1

　 又解：在△ABC中　 ∵ÐC>90°　 ∴C必在以AB為直徑的⊙O內(如圖)

　　 設CD = h，C’D = h’，AD = p，BD = q，

2．設a，bÎ(,)，tana、tanb是一元二次方程的兩個根，求 a + b

解：由韋達定理：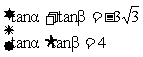

∴

又由a，bÎ(,)且tana，tanb < 0　 (∵tana+tanb<0, tanatanb >0)

得a + bÎ (-p, 0)　　 ∴a + b =

例1 　　若tana=3^x，tanb=3^-x,　 且a-b=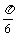，求x的值

解：tan(a-b)=tan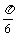=　　　 ∵tana=3^x，tanb=3^-x

∴

∴3•3^x-3•3^-x=2 　　即：

∴(舍去)　　　　 ∴

例2 已知銳角a, b, g 滿足sina+sing=sinb,　 cosa-cosg=cosb,　 求a-b的值

解： ∵sina+sing=sinb　　　 ∴sina -sinb = -sing <0　　　　　　 ①

　∴sina <sinb　　　　　　　 ∴a<b

同理：∵cosa-cosg=cosb　　　 ∴ cosa- cosb = cosg 　②

①²+②²: 1+1-2cos(a-b)=1　　　　 ∴cos(a-b)=

∵　　 　　　∴　 ∴a-b=

　 　例3 已知tana，tanb是關于x的方程的兩個實根，求tan(a+b)的取值范圍

　 解：∵tana，tanb是方程的兩個實根

　∴△=4(7m-3)-8m²≥0　　 ∴2m²-7m+3≤0　　 解之：≤m≤3

　又　　　 ∴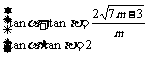

　為求范圍：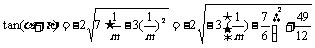

　　 　∵≤m≤3　　　 ∴≤m≤2

　　 　∴當時，有最大值

　　 　當或時，有最小值2

　　 　　∴　　

即　

　　　　　 ∴p-q+1=0

例4　 若，求f (x)=sinx+cosx的最大值和最小值，并求出此時的x值

　解： f (x)=sinx+cosx=2

∵　　　　　 ∴

∴　　　

　即　 　　

當且僅當 ，時 f (x)_min=

當且僅當 ，時 f (x)_max=2　　

例5　 已知f (x)=-acos2x-asin2x+2a+b，其中a>0，xÎ[0,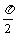]時，

-5≤f (x)≤1，設g(t)=at²+bt-3，tÎ[-1,0]，求g(t)的最小值

　　 　解： f (x)=-acos2x-asin2x+2a+b=-2a[sin2x+cos2x]+2a+b

　　　　　　 =-2asin(2x+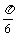)+2a+b

　　　 　∵xÎ[0,]　　　　 ∴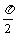　　　

∴

　　 又 a>0　　 ∴-2a<0　　　 ∴

　　　　　　　 ∴　　　

∴

　　　　　　　 ∵-5≤f (x)≤1　　　　 ∴

　　　　　　　 ∴g(t)=at²+bt-3=2t²-5t-3=2(t-)²-　　

∵tÎ[-1,0]

　　　　　　　　 ∴當t=0時，g(t)_min=g(0)=-3

1．兩角和與差的正、余弦公式

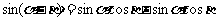
20、(本題滿分16分)

已知數列，設 ，數列。

　 (1)求證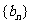：是等差數列；

　 (2)求數列的前n項和S_n；

　 (3)若一切正整數n恒成立，求實數m的取值范圍.

19．(本題滿分16分)已知函數f(x)=alnx―ax―3(a∈R)．

(1)求函數f(x)的單調區間；

(2)若函數y＝f(x)的圖象在點(2，f(2))處的切線的傾斜角為45°，對于任意t∈[1，2]，

函數g(x)=x³+x²[f′(x)+]在區間(t，3)上總不是單調函數，求m的取值范圍.

18. (本題滿分14分)

某地產開發公司擬在如圖所示夾角為60°的角形區域BAC內進行地產開發。根據市政府要求，此地產開發必須在角形區域的兩邊建一條定長為500m的綠化帶PQ，并且規定由此綠化帶和角形區域圍成的△APQ的面積作為此開發商的開發面積。問開發商如何給P,Q進行選址，才能使自己的開發面積最大？并求最大開發面積。

17．(本題滿分15分)△中，所對的邊分別為，,.

(1)求；　 (2)若,求。

16．(本小題滿分14分)　 已知：命題集合，，且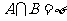

(I)若命題q為真命題，求實數的取值范圍；

(II)若命題，且，試求實數的取值范圍，使得命題有且只有一個為真命題．

15．(本題滿分14分)

已知函數的一系列對應值如下表：

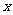
(Ⅰ)根據表格提供的數據求函數的一個解析式；

(Ⅱ)根據(1)的結果，若函數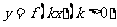周期為，當時，方程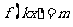恰有兩個不同的解，求實數的取值范圍；