日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

19.(本小題滿分12分)

如圖，在正三棱柱ABC―A₁B₁C₁中，點D是棱AB的中點，BC＝1，AA₁＝.

(1)求證：BC₁∥平面A₁DC；

(2)若記按路線A→C→F→B行駛過程中遇到堵車事件的次數(shù)為ξ，求ξ的分布列及數(shù)學期望Eξ.

18.(本小題滿分12分)

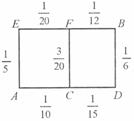
李先生居住在北京的A處，準備開車到鳥巢所在的B處看比賽，若該地各路段發(fā)生堵車事件都是相互獨立的，且在同一路段發(fā)生堵車事件最多只有一次，發(fā)生堵車事件的概率如下圖(例如A→C→D算兩個路段，路段AC發(fā)生堵車事件的概率為，路段CD發(fā)生堵車事件的概率為).

(1)為了能在最短的時間內(nèi)到達鳥巢，請你為李先生選擇一條由A到B的路線，使途中發(fā)生堵車事件的概率最小；

17.(本小題滿分12分)

已知向量a＝(1＋sin 2x，sin x－cos x)，b＝(1，sin x＋cos x)，函數(shù)f(x)＝a?b.

(1)求f(x)的最大值及相應的x的值；

(2)若f(θ)＝，求cos 2(－2θ)的值.

16.已知正態(tài)分布的概率密度函數(shù)f(x)＝e－，x∈(－∞，＋∞)，Φ(1.2)＝0.8848，Φ(0.2)＝0.5793，某正態(tài)總體的概率密度函數(shù)是偶函數(shù)，而且該函數(shù)的最大值為，則σ＝　　　　，總體落入?yún)^(qū)間(－1.2,0.2)的概率為　　　　.

15.已知(1＋x)＋(1＋x)²＋(1＋x)³＋…＋(1＋x)ⁿ＝a₀＋a₁x＋a₂x²＋…＋a_nxⁿ，且a₀＋a₁＋a₂＋…＋a_n＝126，則二項式(3－)ⁿ的展開式中常數(shù)項為　　　　.

14.已知實數(shù)x，y滿足條件則z＝()^x＋y的最小值為　　　　.

13.設雙曲線－＝1(a＞0，b＞0)的離心率為，且它的一條準線與拋物線y²＝4x的準線重合，則此雙曲線的方程為　　　　.

12.已知函數(shù)f(x)＝(a是常數(shù)且a＞0).對于下列命題：

①函數(shù)f(x)的最小值是－1；      ②函數(shù)f(x)在R上是連續(xù)的；

③函數(shù)f(x)在R上存在反函數(shù)； 　④對任意x₁＜0，x₂＜0且x₁≠x₂，恒有f()＜.

其中正確命題的個數(shù)是

A.1       B.2       C.3       D.4

第Ⅱ卷

11.在平行四邊形ABCD中，?＝0，且2²＋²＝1，沿BD折成直二面角A―BD―C，則三棱錐A―BCD的外接球的體積是

A.            B.            C.              D.