
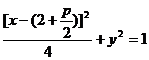 (2)
(2)
是,又從已知條件可得橢圓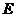 的方程為
的方程為
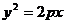 (1)
(1)
例12
直線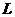 的方程為
的方程為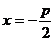 ,其中
,其中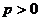 ;橢圓
;橢圓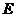 的中心為
的中心為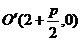 ,焦點在
,焦點在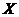 軸上,長半軸為2,短半軸為1,它的一個頂點為
軸上,長半軸為2,短半軸為1,它的一個頂點為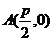 ,問
,問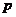 在什么范圍內(nèi)取值時,橢圓上有四個不同的點,它們中的每一點到點
在什么范圍內(nèi)取值時,橢圓上有四個不同的點,它們中的每一點到點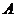 的距離等于該點到直線
的距離等于該點到直線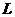 的距離。
的距離。
思路分析 從題目的要求及解析幾何的知識可知,四個不同的點應(yīng)在拋物線
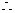
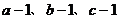 中至少有一個為零,即
中至少有一個為零,即 、
、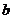 、
、 中至少有一個為1。
中至少有一個為1。
思維障礙 很多學(xué)生只在已知條件上下功夫,左變右變,還是不知如何證明三者中至少有一個為1,其原因是不能把要證的結(jié)論“翻譯”成數(shù)學(xué)式子,把陌生問題變?yōu)槭煜栴}。因此,多練習(xí)這種“翻譯”,是提高轉(zhuǎn)化能力的一種有效手段。
于是 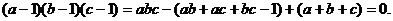
證明 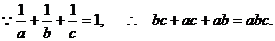
思路分析 結(jié)論沒有用數(shù)學(xué)式子表示,很難直接證明。首先將結(jié)論用數(shù)學(xué)式子表示,轉(zhuǎn)化成我們熟悉的形式。 、
、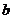 、
、 中至少有一個為1,也就是說
中至少有一個為1,也就是說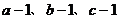 中至少有一個為零,這樣,問題就容易解決了。
中至少有一個為零,這樣,問題就容易解決了。
例11 已知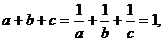 求證
求證 、
、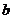 、
、 中至少有一個等于1。
中至少有一個等于1。
思維阻礙 由于這是一個關(guān)于自然數(shù)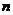 的命題,一些學(xué)生都會想到用數(shù)學(xué)歸納法來證明,難以進(jìn)行數(shù)與形的聯(lián)想,原因是平時不注意代數(shù)與幾何之間的聯(lián)系,單純學(xué)代數(shù),學(xué)幾何,因而不能將題目條件的數(shù)字或式子特征與直觀圖形聯(lián)想起來。
的命題,一些學(xué)生都會想到用數(shù)學(xué)歸納法來證明,難以進(jìn)行數(shù)與形的聯(lián)想,原因是平時不注意代數(shù)與幾何之間的聯(lián)系,單純學(xué)代數(shù),學(xué)幾何,因而不能將題目條件的數(shù)字或式子特征與直觀圖形聯(lián)想起來。
(3) 問題轉(zhuǎn)化的訓(xùn)練
我們所遇見的數(shù)學(xué)題大都是生疏的、復(fù)雜的。在解題時,不僅要先觀察具體特征,聯(lián)想有關(guān)知識,而且要將其轉(zhuǎn)化成我們比較熟悉的,簡單的問題來解。恰當(dāng)?shù)霓D(zhuǎn)化,往往使問題很快得到解決,所以,進(jìn)行問題轉(zhuǎn)化的訓(xùn)練是很必要的。
1 轉(zhuǎn)化成容易解決的明顯題目
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com