日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

2．掌握用圖象求解不等式的方法．

學習難點

　　 圖象法求解不等式中自變量取值范圍的確定．

預習問題

　　 我們來看下面兩個問題有什么關系？

1．理解一元一次不等式與一次函數的轉化關系及本質聯系．

2．解關于x的不等式kx+b>mx+n可以轉化為：

　　 (1)當自變量x取何值時，直線y=(k-m)x+b-n上的點在x軸的上方．

　　 或(2)求當x取何值時，直線y=kx+b上的點在直線y=mx+n上相應的點的上方．(不等號為“<”時是同樣的道理)

學習重點

1．解一元一次不等式可以看作是:當一次函數值大于(或小于)0時，求自變量相應的取值范圍．

11.3.2 一次函數與一元一次不等式

學習目標

5．5.10cm

2．略　 3．5.015cm　 4．41.12mm

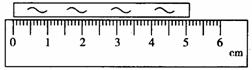
5．如圖所示為測量一金屬筒時刻度尺示數的示意圖，該金屬筒長度為　 　　　cm.

答案：1．△x=(12.6-12. 4) mm= 0. 2 mm；

η=△x / x₀ =1. 6%

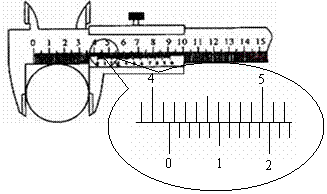
4．用游標為50分度的卡尺測量某圓柱的直徑時，卡尺上的示數如圖9所示,可讀出圓柱的直徑為

　　　　 　mm

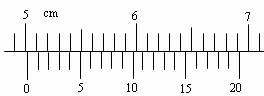
3．讀出如圖所示游標尺的讀數．