
14. 設復數z=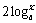 +
+ ,
,
問當x為何實數時,z是⑴實數, ⑵ 虛數, ⑶ 純虛數, ⑷ z在復平面上對應的點在實軸上方,⑸|z|=1
解:⑴當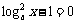 ,即x=a或
,即x=a或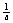 時z為實數;
時z為實數;
⑵當 ,即
,即 且
且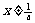 時z為虛數;
時z為虛數;
⑶當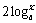 =0且
=0且 ,即x=1時z為純虛數
,即x=1時z為純虛數
⑷.若0<a<1,則0<x<a或x>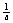 ;若a>1,則x>a或0<x<
;若a>1,則x>a或0<x<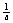 時z對應的點在實軸上方;
時z對應的點在實軸上方;
⑸當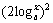 +
+ =1即x=1時,|z|=1
=1即x=1時,|z|=1
[探索題]設z是虛數,ω=z+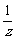 是實數,且-1<ω<2
是實數,且-1<ω<2
(1)求|z|的值及z的實部的取值范圍;
(2)設u=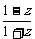 ,求證:u為純虛數;
,求證:u為純虛數;
(3)求ω-u2的最小值
解(1):設z=a+bi(a、b∈R,b≠0),
則ω=a+bi+ =(a+
=(a+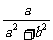 )+(b-
)+(b-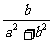 )i
)i
∵ω是實數,b≠0,
∴a2+b2=1,即|z|=1
∵ω=2a,-1<ω<2,
∴z的實部的取值范圍是(- ,1)
,1)
(2)證明:u=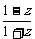 =
=
= =-
=-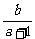 i
i
∵a∈(- ,1),b≠0,
,1),b≠0,
∴u為純虛數
(3)解:ω-u2=2a+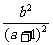
=2a-1+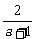
=2[(a+1)+ ]-3
]-3
∵a∈(- ,1),∴a+1>0
,1),∴a+1>0
∴ω-u2≥2×2-3=1
當a+1= ,即a=0時,上式取等號
,即a=0時,上式取等號
∴ω-u2的最小值為1
13. 已知 ,且復數
,且復數 的虛部減去它的實部所得的差等于
的虛部減去它的實部所得的差等于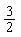 ,求復數
,求復數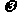 的模;
的模;
解. 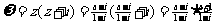

即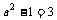

12. 已知復數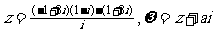 當
當 求a的取值范圍,
求a的取值范圍,
解:
因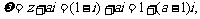


故a的取值范圍是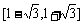
11.已知z是復數,z+2i、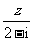 均為實數(i為虛數單位),且復數(z+ai)2在復平面上對應的點在第一象限,求實數a的取值范圍
均為實數(i為虛數單位),且復數(z+ai)2在復平面上對應的點在第一象限,求實數a的取值范圍
解:設z=x+yi(x、y∈R),
∴z+2i=x+(y+2)i,由題意得y=-2
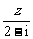 =
=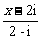 =
=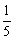 (x-2i)(2+i)=
(x-2i)(2+i)=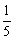 (2x+2)+
(2x+2)+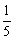 (x-4)i
(x-4)i
由題意得x=4,∴z=4-2i
∵(z+ai)2=(12+4a-a2)+8(a-2)i,
根據條件,已知 解得2<a<6,
解得2<a<6,
∴實數a的取值范圍是(2,6)
10.若復數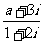 (a∈R,i為虛數單位位)是純虛數,則實數a的值為_____
(a∈R,i為虛數單位位)是純虛數,則實數a的值為_____
◆練習簡答:1-4.DDDB; 5.-i
; 6.0; 7.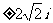 ; 8.
; 8. ; 9.
; 9.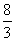 ; 10.-6.
; 10.-6.
[解答題]
9.若 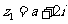 ,
, 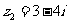 ,且
,且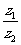 為純虛數,則實數a的值為___ .
為純虛數,則實數a的值為___ .
8.(2005全國Ⅲ).已知復數z0=3+2i,
復數z滿足z z0=3z+z0,則z=
z0=3z+z0,則z=
7.(2006廣東) 若復數 滿足方程
滿足方程 ,則
,則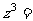 _______
_______
6. (2005湖南)復數z=i+i2+i3+i4+……+i2008=__________
5.(2005全國Ⅰ)復數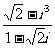 的共軛復數是 ________
的共軛復數是 ________
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com