日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

例1．求函數(shù)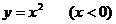的反函數(shù),并利用對稱關(guān)系作出其反函數(shù)的圖象.

解：∵原函數(shù)的定義域是x<0，值域是y>0,

∴由y=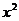解出,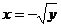

∴函數(shù)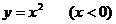的反函數(shù)是,

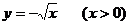作 y=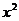(x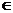(-∞,0))的圖象，再作該函數(shù)關(guān)于直線y=x的對稱曲線，即為函數(shù)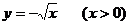的圖象(如圖).

例2．求函數(shù)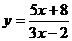的值域．

分析：靈活運(yùn)用互為反函數(shù)的兩個(gè)函數(shù)定義域和值域之間的關(guān)系.

解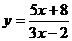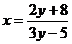：∵　　 ∴　　 ∴　 y≠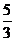

∴函數(shù)的值域?yàn)閧y|y≠}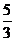

例3 已知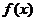=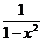(x<-1)，求；

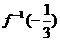解法1：⑴令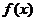=y=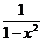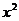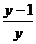，∴=--①，∵x<-1，∴x=-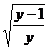;⑵∵x<-1，由①式知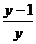≥1,∴y<0;

⑶∴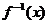= -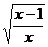(x<0)；⑷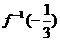=-2.

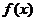分析：由y=與y=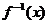互為反函數(shù)的關(guān)系可知：當(dāng)y=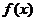中的x=a時(shí)y=b，則在y=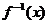中,當(dāng)x=b時(shí)y=a，本題要求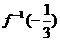，設(shè)其為u，說明在函數(shù)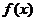=y=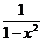(x<-1)中，當(dāng)y=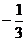時(shí)，x=u，問題轉(zhuǎn)化為知原來函數(shù)中的y=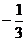而求x.

解法2：令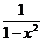=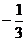，變形得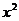=1+3=4，又∵x<-1，∴x=-2.

說明：解法2顯然比解法1簡捷得多，正確靈活地運(yùn)用所學(xué)的有關(guān)概念，往往可以收到事半功倍的效果.

3．應(yīng)用：⑴利用對稱性作反函數(shù)的圖像

若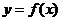的圖象已作出或比較好作，那么它的反函數(shù)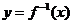的圖象可以由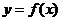的圖象關(guān)于直線y=x對稱而得到；

⑵求反函數(shù)的定義域求原函數(shù)的值域；

⑶反函數(shù)的單調(diào)性與原函數(shù)的單調(diào)性相同

2．證明結(jié)論(不要求掌握，根據(jù)實(shí)際情況處理)

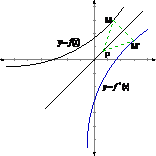證明：設(shè)M(a,b)是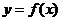的圖象上的任意一點(diǎn)，

則當(dāng)x=a時(shí)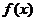，有唯一的值.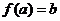

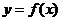∵有反函數(shù)，

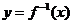∴當(dāng)x=b時(shí)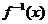，有唯一的值，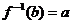

即點(diǎn)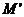(b,a)在反函數(shù)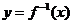的圖象上.

若a=b，則M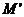，是直線y=x上的同一個(gè)點(diǎn)，它們關(guān)于直線y=x對稱.

若a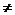b，在直線y=x上任意取一點(diǎn)P(c,c)，連結(jié)PM，P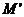，M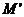

由兩點(diǎn)間的距離公式得：

PM=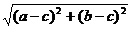,P=，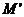

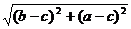∴PM=P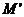.　 ∴直線y=x是線段M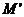的垂直平分線，

∴點(diǎn)M, 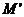關(guān)于直線y=x對稱.

∵點(diǎn)M是y=f(x)的圖象上的任意一點(diǎn)，

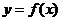∴圖象上任意一點(diǎn)關(guān)于直線y=x的對稱點(diǎn)都在它的反函數(shù)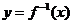的圖象上，由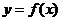與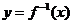互為反函數(shù)可知，函數(shù)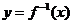圖象上任意一點(diǎn)關(guān)于直線y=x的對稱點(diǎn)也都在它的反函數(shù)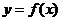的圖象上，

∴函數(shù)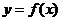與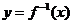的圖象關(guān)于直線y=x對稱.

逆命題成立：若兩個(gè)函數(shù)的圖象關(guān)于直線y=x對稱，則這兩個(gè)函數(shù)一定是互為反函數(shù).

1．探究互為反函數(shù)的函數(shù)的圖像關(guān)系

觀察討論函數(shù)、反函數(shù)的圖像，歸納結(jié)論：函數(shù)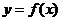的圖象和它的反函數(shù)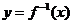的圖象關(guān)于直線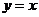對稱.

5.我們已經(jīng)知道兩個(gè)互為反函數(shù)的函數(shù)間有著必然的聯(lián)系(在定義域、值域和對應(yīng)法則方面). 函數(shù)圖象是從“形”的方面反映這個(gè)函數(shù)的自變量x與因變量y之間的關(guān)系.因此，互為反函數(shù)的函數(shù)圖象間也必然有一定的關(guān)系，今天通過觀察如下圖像研究-互為反函數(shù)的函數(shù)圖象間的關(guān)系.

①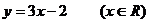的反函數(shù)是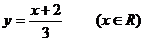

②的反函數(shù)是

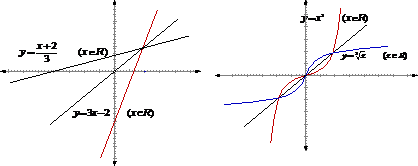
4. 在平面直角坐標(biāo)系中，①點(diǎn)A(x,y)關(guān)于x軸的對稱點(diǎn)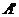(x,-y);

②點(diǎn)A(x,y)關(guān)于y軸的對稱點(diǎn)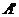(-x,y);③點(diǎn)A(x,y)關(guān)于原點(diǎn)的對稱點(diǎn)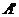(-x,-y);④點(diǎn)A(x,y)關(guān)于y=x軸的對稱點(diǎn)(?,？);

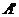3．反函數(shù)的求法：一解、二換、三注明

2．互為反函數(shù)的兩個(gè)函數(shù)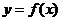與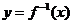間的關(guān)系：

----定義域、值域相反，對應(yīng)法則互逆；

1．反函數(shù)的定義；

2.附加隱含條件的應(yīng)用規(guī)律

⑴溶液無色透明時(shí)，則溶液肯定無有色離子。如Cu²⁺(藍(lán)色)、Fe³⁺(棕黃色)、Fe²⁺(淺綠色)、(紫紅色)等都有顏色，若無色溶液則說明這些離子不存在。

⑵強(qiáng)堿性溶液中肯定不存在與起反應(yīng)的離子。

⑶強(qiáng)酸性溶液中肯定不存在與H⁺起反應(yīng)的離子

⑷與水反應(yīng)的離子，如O^2-、N^3-、P^3-等在水溶液中不存在。

試題枚舉

[例1]下列離子方程式正確的是

A．NaHSO₃溶液與NaOH溶液反應(yīng)：HSO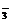+OH^－＝S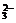O+H₂O

B．少量二氧化碳通入足量的NaOH溶液：CO₂+OH^－＝

C．Fe與鹽酸反應(yīng)產(chǎn)生H₂：2Fe+6H⁺＝2Fe³⁺+3H₂↑

D．氨水和醋酸溶液混合NH₃·H₂O+CH₃COOH＝NH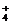+CH₃COO^－+H₂O

解析: 判斷離子方程式的正誤應(yīng)注意①是否符合客觀實(shí)際；②應(yīng)該用化學(xué)式表示的(氣體、沉淀、水、弱酸、弱堿、氧化物、單質(zhì)等)是否寫對，應(yīng)該刪掉的離子是否刪去；③是否配平，電子轉(zhuǎn)移是否合理．

據(jù)此檢查各選項(xiàng)，A、D正確．B錯(cuò)，因少量的CO₂通入足量的NaOH溶液中，應(yīng)生成CO．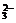

正確的寫法為：CO₂+2OH^－＝C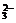O+H₂O

C錯(cuò)．因不符合客觀實(shí)際，應(yīng)生成Fe²⁺．

正確的寫法為：Fe+2H⁺＝Fe²⁺+H₂↑

答案: AD

[例2.]下列各組離子中，能在強(qiáng)酸溶液里大量共存，并且溶液呈無色透明的是

A．MnO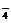，K⁺，Na⁺，SO　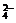　　　　 B．Na⁺，K⁺，HCO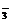，Cl^－

C．Mg²⁺，NH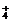，Cl^－，NO　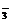　　　　 D．Ba²⁺，K⁺，S^2－，SO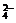

解析：對于離子能否共存問題：必須考慮兩個(gè)問題，一看同組離子是否發(fā)生反應(yīng)(復(fù)分解或氧化還原)，二看是否滿足題干要求．

有顏色離子：Fe³⁺，F(xiàn)e²⁺，Cu²⁺，MnO……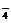

強(qiáng)酸性(或強(qiáng)堿性)，說明溶液中除離子組內(nèi)各離子外，還應(yīng)有H⁺或(OH^－)，典型的氧化性離子(如Fe³⁺,Mn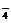O,Cr₂O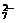等)和典型的還原性離子(如Fe²⁺，S^2－，I^－，SO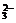等)在溶液中會發(fā)生氧化還原反應(yīng)．據(jù)以上分析得此題正確選項(xiàng)為C．

答案：C

[例3](1)向NaHSO₄溶液中，逐滴加入Ba(OH)₂溶液中至中性，請寫出發(fā)生反應(yīng)的離子方程式：　　　　　　　　　　　　　　　　　　　　　 。

(2)在以上中性溶液中，繼續(xù)滴加Ba(OH)_2­溶液，請寫出此步反應(yīng)的離子方程式　　　　　　　　　　　　　　　　　　 。

解析：題目要求NaHSO₄溶液與Ba(OH)₂溶液反應(yīng)呈中性，也即要求寫出的離子方程式屬于下列反應(yīng) 2NaHSO₄　 +　 Ba(OH)₂ = 2H₂O + Na₂SO₄ + BaSO₄↓。則離子方程式為：2H⁺ + SO₄^2- + Ba²⁺ + 2OH^- =　 BaSO₄ ↓ + 2H₂O 。若向上述溶液中繼續(xù)滴加B(OH)₂，則有 Ba²⁺ + SO₄^2-　 =　 BaSO₄ ↓

答案：2H⁺ + SO₄^2- + Ba²⁺ + 2OH^- =　 BaSO₄ ↓ + 2H₂O

　　　　 Ba²⁺ + SO₄^2-　 =　 BaSO₄ ↓