
2.集合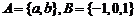 ,從A到B的映射f滿足
,從A到B的映射f滿足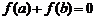 ,那么這樣的映射
,那么這樣的映射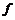
的個數有( )
A.2個 B.3個 C.5個 D.8個
1.設a,b為實數,若復數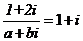 ,則
,則
A.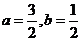 B.
B. 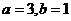 C.
C. 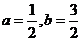
 D.
D. 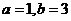
反函數的定義及其注意點、求法步驟
(1)
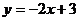 (x∈R) (2)
(x∈R) (2)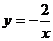 (x∈R,且x≠0)
(x∈R,且x≠0)
(3)
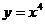 (x≥0) (4)
(x≥0) (4)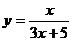 (x∈R,且x≠
(x∈R,且x≠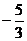 )
)
例1.求下列函數的反函數:
①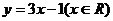 ;
②
;
②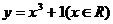 ;
;
③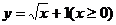 ; ④
; ④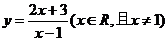 .
.
解:①由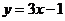 解得
解得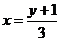
∴函數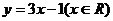 的反函數是
的反函數是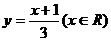 ,
,
②由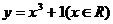 解得x=
解得x=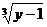 ,
,
∴函數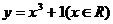 的反函數是
的反函數是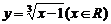
③由y=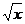 +1解得x=
+1解得x=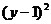 ,
,
∵x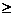 0,∴y
0,∴y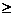 1.
1.
∴函數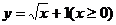 的反函數是x=
的反函數是x=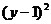 (x
(x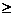 1);
1);
④由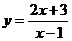 解得
解得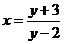
∵xc{x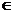 R|x
R|x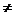 1},∴y
1},∴y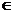 {y
{y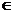 R|y
R|y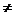 2}
2}
∴函數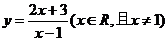 的反函數是
的反函數是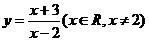
小結:⑴求反函數的一般步驟分三步,一解、二換、三注明
⑵反函數的定義域由原來函數的值域得到,而不能由反函數的解析式得到
⑶求反函數前先判斷一下決定這個函數是否有反函數,即判斷映射是否是一一映射
例2.求函數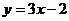 (
(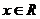 )的反函數,并畫出原來的函數和它的反函數的圖像
)的反函數,并畫出原來的函數和它的反函數的圖像
解:由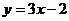 解得
解得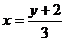
 ∴函數
∴函數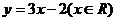 的反函數是
的反函數是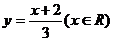 ,
,
它們的圖像為:
例3求函數 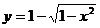
(-1<x<0)的反函數
解:∵ -1<x<0 ∴0<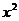 <1 ∴0<1 -
<1 ∴0<1 -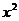 < 1
< 1
∴
0 < < 1 ∴0 < y <1
< 1 ∴0 < y <1
由: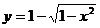 解得:
解得: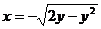 (∵ -1< x < 0 )
(∵ -1< x < 0 )
∴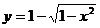 (-1<x < 0)的反函數是:
(-1<x < 0)的反函數是: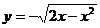 (0<x<1 )
(0<x<1 )
例4 已知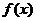 =
= 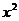 -2x(x≥2),求
-2x(x≥2),求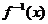 .
.
解法1:⑴令y=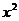 -2x,解此關于x的方程得
-2x,解此關于x的方程得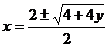 ,
,
∵x≥2,∴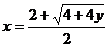 ,即x=1+
,即x=1+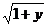 --①,
--①,
⑵∵x≥2,由①式知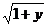 ≥1,∴y≥0--②,
≥1,∴y≥0--②,
⑶由①②得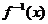 =1+
=1+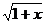 (x≥0,x∈R);
(x≥0,x∈R);
解法2:⑴令y=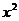 -2x=
-2x=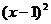 -1,∴
-1,∴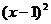 =1+y,
=1+y,
∵x≥2,∴x-1≥1,∴x-1=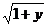 --①,即x=1+
--①,即x=1+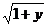 ,
,
⑵∵x≥2,由①式知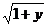 ≥1,∴y≥0,
≥1,∴y≥0,
⑶∴函數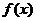 =
= 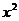 -2x(x≥2)的反函數是
-2x(x≥2)的反函數是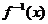 =1+
=1+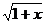 (x≥0);
(x≥0);
說明:二次函數在指定區間上的反函數可以用求根公式反求x,也可以用配方法求x,但開方時必須注意原來函數的定義域.
反函數的定義
一般地,設函數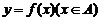 的值域是C,根據這個函數中x,y 的關系,用y把x表示出,得到x=
的值域是C,根據這個函數中x,y 的關系,用y把x表示出,得到x=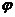 (y). 若對于y在C中的任何一個值,通過x=
(y). 若對于y在C中的任何一個值,通過x=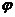 (y),x在A中都有唯一的值和它對應,那么,x=
(y),x在A中都有唯一的值和它對應,那么,x=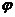 (y)就表示y是自變量,x是自變量y的函數,這樣的函數x=
(y)就表示y是自變量,x是自變量y的函數,這樣的函數x=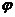 (y) (y
(y) (y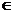 C)叫做函數
C)叫做函數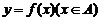 的反函數,記作
的反函數,記作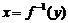 ,習慣上改寫成
,習慣上改寫成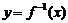
開始的兩個例子:s=vt記為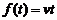 ,則它的反函數就可以寫為
,則它的反函數就可以寫為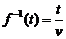 ,同樣
,同樣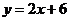 記為
記為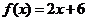 ,則它的反函數為:
,則它的反函數為: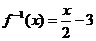 .
.
探討1:所有函數都有反函數嗎?為什么?
反函數也是函數,因為它符合函數的定義,從反函數的定義可知,對于任意一個函數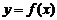 來說,不一定有反函數,如
來說,不一定有反函數,如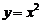 ,只有“一一映射”確定的函數才有反函數,
,只有“一一映射”確定的函數才有反函數,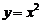 ,
,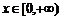 有反函數是
有反函數是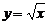
探討2:互為反函數定義域、值域的關系
從映射的定義可知,函數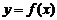 是定義域A到值域C的映射,而它的反函數
是定義域A到值域C的映射,而它的反函數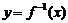 是集合C到集合A的映射,因此,函數
是集合C到集合A的映射,因此,函數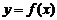 的定義域正好是它的反函數
的定義域正好是它的反函數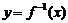 的值域;函數
的值域;函數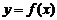 的值域正好是它的反函數
的值域正好是它的反函數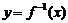 的定義域
的定義域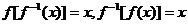 (如下表):
(如下表):
|
|
函數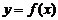 |
反函數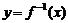 |
|
定義域 |
A |
C |
|
值 域 |
C |
A |
探討3: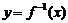 的反函數是?
的反函數是?
若函數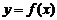 有反函數
有反函數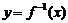 ,那么函數
,那么函數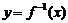 的反函數就是
的反函數就是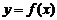 ,這就是說,函數
,這就是說,函數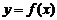 與
與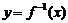 互為反函數
互為反函數
我們知道,物體作勻速直線運動的位移s是時間t的函數,即s=vt,其中速度v是常量,定義域t 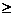 0,值域s
0,值域s 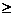 0;反過來,也可以由位移s和速度v(常量)確定物體作勻速直線運動的時間,即
0;反過來,也可以由位移s和速度v(常量)確定物體作勻速直線運動的時間,即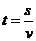 ,這時,位移s是自變量,時間t是位移s的函數,定義域s
,這時,位移s是自變量,時間t是位移s的函數,定義域s 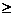 0,值域t
0,值域t 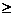 0.
0.
又如,在函數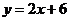 中,x是自變量,y是x的函數,定義域x
中,x是自變量,y是x的函數,定義域x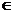 R,值域y
R,值域y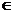 R. 我們從函數
R. 我們從函數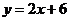 中解出x,就可以得到式子
中解出x,就可以得到式子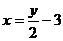 . 這樣,對于y在R中任何一個值,通過式子
. 這樣,對于y在R中任何一個值,通過式子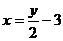 ,x在R中都有唯一的值和它對應. 因此,它也確定了一個函數:y為自變量,x為y的函數,定義域是y
,x在R中都有唯一的值和它對應. 因此,它也確定了一個函數:y為自變量,x為y的函數,定義域是y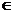 R,值域是x
R,值域是x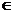 R.
R.
綜合上述,我們由函數s=vt得出了函數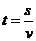 ;由函數
;由函數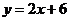 得出了函數
得出了函數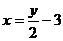 ,不難看出,這兩對函數中,每一對中兩函數之間都存在著必然的聯系:①它們的對應法則是互逆的;②它們的定義域和值域相反:即前者的值域是后者的定義域,而前者的定義域是后者的值域. 我們稱這樣的每一對函數是互為反函數.
,不難看出,這兩對函數中,每一對中兩函數之間都存在著必然的聯系:①它們的對應法則是互逆的;②它們的定義域和值域相反:即前者的值域是后者的定義域,而前者的定義域是后者的值域. 我們稱這樣的每一對函數是互為反函數.
28.(1)材料一、二兩種治國思想的不同點?(2分)
(2)材料三、四兩種主張的共同之處是什么?差別又在哪里?實施結果如何?(10分)
(3)幾則材料折射出此間中國古代思想領域呈現怎樣的發展趨勢?分別反映了哪些實質性問題?(4分)
27.(1)概括兩漢與宋代教育的共同特點,相對于封建官學,書院教學的有哪些優勢?(7分)
(2)明清時期江南教育較前代出現哪些變化?分析的變化原因?(10分)
26.(1)材料二與材料一對比,相同的主張是什么?適應了怎樣的時代要求?(5分)
(2)材料二比材料一又有哪些重要發展,其積極意義何在?(6分)
(3)黃宗羲對中國提出了怎樣的政治設計? 這種設計的歷史缺陷何在?造成這種缺陷的根本原因是什么? (6分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com