日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

22．(14分)已知函數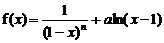，其中n∈N+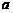，為常數。

①當n=2時，求函數f(x)的極值；

②當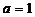時，證明：對任意的正整數n，當x≥2時，。

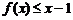21．(12分)已知二次函數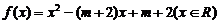，同時滿足：①不等式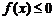的解集有且只有一個元素；②在定義域內存在x₁、x₂，使得x₁+x₂=0，但f(x₁) ≠f(x₂)，設數列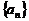的前n項和S_n=f(n)。

①求f(x)的表達式；

②求數列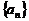的通項公式。

③若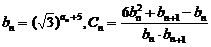，數列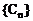的前n項和為T_n ，T_n＞n+m，對n∈N⁺，n≥2恒成立，求m的范圍。

20．(12分)設F₁、F₂分別是橢圓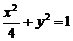的左、右焦點。

①若P是該橢圓上的一個動點，求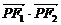的最大值和最小值；

②設過定點M(0，2)的直線L與橢圓交于不同的兩點A、B，且∠AOB為銳角(其中O為坐標原點)，求直線L的斜率k的取值范圍。

19．(12分)如圖，正三棱柱ABC-A₁B₁C₁中，D是BC的中點，AA₁=AB=1.

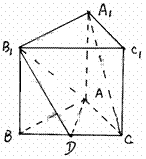①求證：A₁C∥平面AB₁D；

②求二面角B-AB₁-D的大小；

③求點C到平面AB₁D的距離。

18．(12分)有甲、乙、丙、丁四名乒乓球運動員，通過對他們過去成績的統計，在一場比賽中，甲對乙、丙、丁，甲取勝的概率分別為0.6、0.8、0.9。

①若四名運動員每兩人之間進行一場比賽，求甲恰好取勝兩場的概率；

②若四名運動員每兩人之間進行一場比賽，設甲獲勝場次為ξ，求隨機變量ξ的分布列及期望Eξ。

17．(12分)已知0是坐標原點，，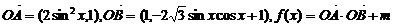

①求f(x)的單調遞增區間；

②若f(x)的定義域為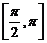，值域為[2，5]，求m的值。

16．已知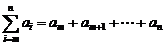(其中m，n∈Z且0≤m＜n)，設 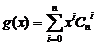，函數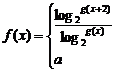　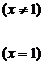 ，在x=1處連續，則實數a的值_______________

15．已知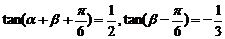，則=_______________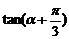

14．已知數列{a_n}是二項式(2+3x)ⁿ(n≥2，n∈N⁺) 展開式的第3項的二項式系數，S_n是數列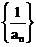的前n項和，則_______________

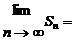13．“x＞1”是“x²＞1”的_______________條件。