
例9:下列屬于新型無機非金屬材料的特性的是( )
①耐高溫、高強度 ②具有光學特性 ③具有電學特性
④具有生物功能 ⑤可塑性好
A.① B.①②③ C.①②③④ D.①②③⑤
分析:本題屬于識記性考查,只要對課本知識掌握,便可準確回答。
答案:C
例8:普通玻璃的主要成分為Na2CaSi6O14,以氧化物的形式可表示為___________;鉀云母的化學式為K2H4Al6Si6O24,以氧化物的形式可表示為___________;正長石的化學式為KAlSi3Ox,x的數值為___________,以氧化物的形式可表示為___________。
解析:硅酸鹽以氧化物的形式可表示為活潑金屬氧化物·較活潑金屬氧化物·SiO2·H2O,所以普通玻璃Na2CaSi6O14-Na2O·CaO·6SiO2;鉀云母K2H4Al6Si6O24-K2O·3Al2O3·6SiO2·2H2O;正長石KAlSi3Ox-K2O·Al2O3·6SiO2,則x=8。
例6:二氧化硅的熔沸點較高的原因是( )
A.二氧化硅中,硅氧原子個數之比為1:2
B.二氧化硅晶體是立體網狀的原子晶體
C.二氧化硅中,Si-O鍵的鍵能大
D.二氧化硅晶體中原子以共價鍵相結合
分析:本題涉及二氧化硅晶體結構的重點知識。二氧化硅的熔沸點較高的原因,是由于其晶體中Si-O鍵的鍵能很高,并形成了一種立體網狀的原子晶體,熔融SiO2晶體需消耗較多的能量。
答案:BC
例7:物質A是一種高熔點化合物,不溶于硫酸、硝酸等強酸。A與純堿熔融反應,生成化合物B,同時放出氣體C;把氣體C通入B的溶液中,則得到化合物D;D在干燥空氣中轉變為化合物E;將E加熱又得到化合物A。試寫出A、B、C、D、E的化學式:A__________、B__________、C__________、D__________、E__________。
分析:本題應根據對實驗現象的分析,得出結論。A是不溶于硫酸、硝酸等強酸的高熔點化合物,它能與純堿熔融反應,而且放出氣體C,初步判斷A可能是SiO2,B可能是Na2SiO3,C可能CO2。若把CO2通入Na2SiO3溶液中,會得到膠狀沉淀H4SiO4,H4SiO4在干燥空氣中易脫水生成H2SiO3,H2SiO3只有加熱才能生成SiO2。這些都是與題目所給出的實驗現象相符合,這就證實A確實是SiO2,那么其他物質的推斷就迎刃而解。
答案:SiO2 Na2SiO3 CO2 H4SiO4 H2SiO3
例4:下列分子或晶體均不屬于正四面體結構的是( )
①二氧化碳 ②晶體硅 ③金剛石 ④甲烷 ⑤氨氣
A.①③ B.②④ C.①⑤ D.③④
分析:此題是對常見物質結構的考查,平時學習中注意對這些內容的理解和記憶,就能輕而易舉地得出答案。二氧化碳是直線形分子,晶體硅、甲烷和金剛石是正四面體結構,氨氣是三角錐形分子。
答案:C
例5:下列關于硅的說法不正確的是( )
A.晶體硅是灰黑色有金屬光澤的固體
B.硅是良好的半導體材料
C.硅的性質很不活潑,常溫下不與任何物質反應
D.在加熱時,硅能與H2、O2等非金屬反應
分析:熟練掌握硅的物理性質和化學性質,硅在常溫下可與NaOH溶液、氫氟酸等反應。
答案:C
例3:下列碳的化合物其穩定性的順序排列正確的是( )
①CaCO3 ②Ca(HCO3)2 ③H2CO3 ④CO2
A.①>②>③>④ B.①>②>④>③
C.④>①>②>③ D.①>③>②>④
分析:應用實驗推理法H2CO3常溫下就可以分解生成CO2和H2O;Ca(HCO3)2加熱時分解生成CaCO3、CO2和H2O;而CaCO3則需高溫才分解生成CaO和CO2,這說明CO2在高溫下不分解。由上述實驗可知CO2是最穩定的,其次是CaCO3,再其次是Ca(HCO3)2,而最不穩定的是H2CO3。
答案:C
例1:在碳族元素中,非金屬性最強的元素是__________,金屬性最強的元素是__________,單質能作半導體的元素是__________,在化合物中+2價最穩定的元素是__________,最穩定的氣態氫化物是__________,酸性最強的最高價氧化物對應水化物是__________。
分析:如果對碳族元素的相似性、遞變性和特殊性能夠熟練掌握,便可輕易解答本題。
答案:碳 鉛 硅 鉛 甲烷 碳酸
例2:如何證明金剛石和石墨是由同一種元素組成的不同單質?
分析:金剛石和石墨的物質性質有較大差異,是不同的單質,但兩者是由同種元素組成的,可根據特定的化學反應,看是否生成同種物質,并從物質的元素組成上進行分析。
答案:把等量的金剛石、石墨少許分別放在純凈的氧氣中燃燒,鑒定生成物的成分,結果發現生成物都是CO2,其中所含C的質量分數相等,說明CO2中的氧元素是氧氣提供的,而碳元素只能來自金剛石和石墨。由此可知金剛石和石墨是由同一種元素組成的兩種不同單質。
1求值:(1)
選題意圖:考查兩角和與差三角函數公式的應用和三角函數關系式的變形能力
解:(1)原式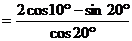
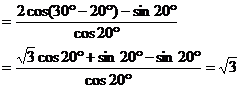
(2)原式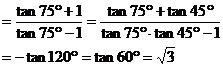
說明:在三角函數關系式的變形過程中,要注意統一角、統一函數,要注意角與角之間的和、差、倍、半關系和特殊角之間的關系等
2已知3sinβ=sin(2α+β)且tanα=1,求tan(α+β) ?
?
選題意圖:考查兩角和與差的三角函數公式的應用和三角函數關系式的變形能力
解:由3sinβ=sin(2α+β)即3sin[(α+β)-α]=[sin(α+β)+α]
得:3sin(α+β)cosα-3cos(α+β)sinα
=sin(α+β)cosα+cos(α+β)sinα
∴2sin(α+β)cosα=4cos(α+β)sinα
∴tan(α+β)=2tanα
又tanα=1 ∴tan(α+β)=2
說明:本題解法的關鍵是要注意到β=(α+β)-α,2α+β=(α+β)+α
3已知方程x2+4ax+3a+1=0(a>1)的兩根分別為tanα,tanβ且α,β∈
(-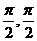 ),求sin2(α+β)+sin(α+β)cos(α+β)+2cos2(α+β)的值
),求sin2(α+β)+sin(α+β)cos(α+β)+2cos2(α+β)的值
選題意圖:考查兩角和三角函數公式和平方關系的應用
解:根據韋達定理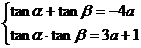
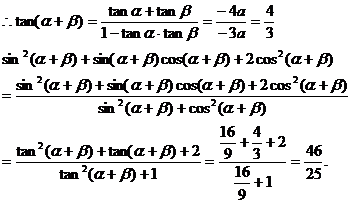
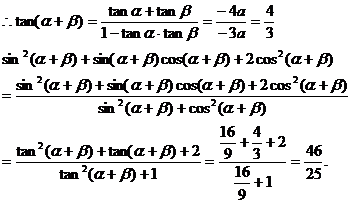
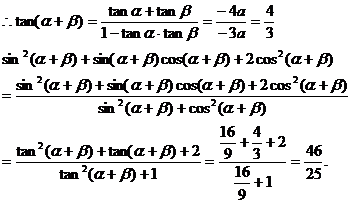
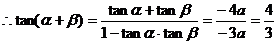
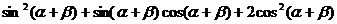
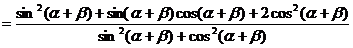
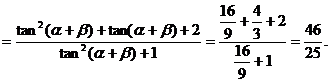
說明:解題的整個過程就是統一角,統一函數的過程
4求sin18°和cos36°的值
解:∵sin36°=cos54°
即sin(2×18°)=cos(3×18°)
2sin18°cos18°=4cos318°-3cos18°
∵cos18°≠0
∴2sin18°=4cos218°-3
整理得4sin218°+2sin18°-1=0
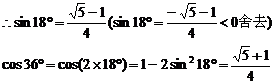
說明:本題通過二倍角和三倍角公式構造了關于sin18°的方程求解,但利用sin54°=cos36°很難解出sin18° 在解決三角函數問題的過程中也要適當注意一些代數方法的使用
在解決三角函數問題的過程中也要適當注意一些代數方法的使用
1 已知函數
已知函數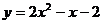 的圖象與
的圖象與 軸交點為
軸交點為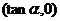 、
、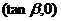 ,
,
求證: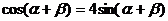 .
.
證明:∵函數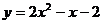 的圖象與
的圖象與 軸交點為
軸交點為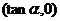 、
、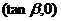
∴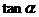 +
+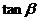 =
=
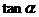
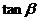 =-1
=-1
∴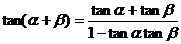 =
=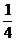
∴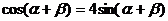 .
.
2 求證:
求證: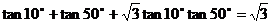
證明:∵

∴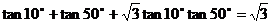
3 求證:
求證: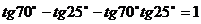
證明:∵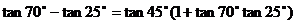
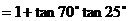
∴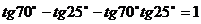
1 已知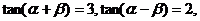 求
求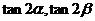 的值.
的值.
分析:若用公式(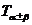 )將已知等式展開,只能得到
)將已知等式展開,只能得到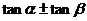 與
與 的等量關系,要得到探求結論十分困難.我們來觀察一下角的特征,
的等量關系,要得到探求結論十分困難.我們來觀察一下角的特征,
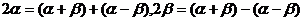 ,
,
于是就可以正確的解法.
歸納:將角作適當的變換,配出有關角,便于溝通條件與結論之間的聯系,這是三角恒等變換中常用的方法之一,這種變換角的方法通常叫配角法.例如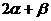 配成
配成 又如
又如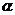 配成
配成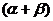 -
-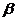 或者
或者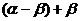 .
.
2 已知 求
求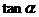 的值.
的值.
3 不查表求值: .
.
分析:
要善于把公式變形后使用,從公式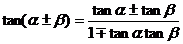 中可得變形公式:
中可得變形公式:
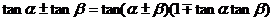 ,這會使解題更具靈活性.
,這會使解題更具靈活性.
 .
.
∴原式=1.
例1 化簡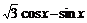
解:原式=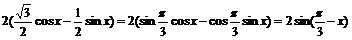
或解:原式=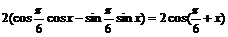
例2 已知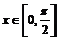 ,求函數
,求函數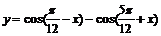 的值域
的值域
解: 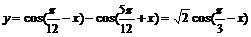
∵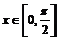 ∴
∴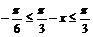
∴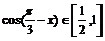 ∴函數y的值域是
∴函數y的值域是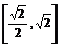
例3 已知 ,
,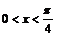 求
求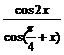 的值
的值
解:∵
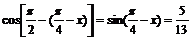
即: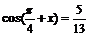
∵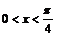 ∴
∴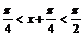
從而
而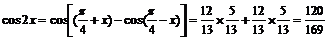
∴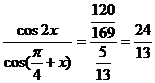
例4 已知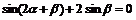 求證tana=3tan(a+b)
求證tana=3tan(a+b)
證:由題設: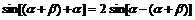
即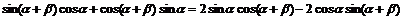
∴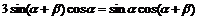
∴tana=3tan(a+b)
例5 已知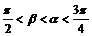 ,
,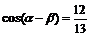 ,
, ,
,
求sin2a的值
解:∵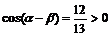
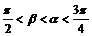
∴ ∴
∴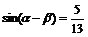
∴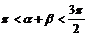
又 ∴
∴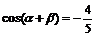
∴sin2a=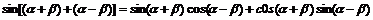
=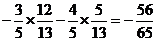
例6證明A+B+C=nπ(n∈Z)的充要條件是tanA+tanB+tanC=tanA·tanB·tanC
選題意圖:考查兩角和與差的正切公式的應用和求角的方法
證明:(先證充分性)
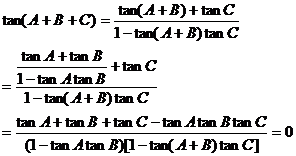
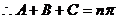 (n∈Z)
(n∈Z)
(再證必要性)
由A+B+C=nπ即A+B=nπ-C
得tan(A+B)=-tanC
tanA+tanB+tanC=tan(A+B)(1-tanAtanB)+tanC
=-tanC(1-tanAtanB)+tanC
=tanAtanBtanC
說明:本題可考慮證明A+B=nπ-C(n∈Z)的充要條件是tanA+tanB+tanC=tanA·tanB·tanC較為簡單
例7求證:tan20°tan30°+tan30°tan40°+tan40°tan20°=1
選題意圖:考查兩角和與差的正切變形公式的應用
證明:左端=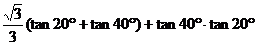

說明:可在△ABC中證明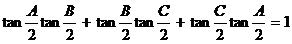

例8已知A、B為銳角,證明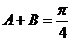 的充要條件是(1+tanA)(1+tanB)=2
的充要條件是(1+tanA)(1+tanB)=2
選題意圖:考查兩角和與差的正切公式的變換應用和求角的方法
證明:(先證充分性)
由(1+tanA)(1+tanB)=2即1+(tanA+tanB)+tanA·tanB=2
得tan(A+B)[1-tanAtanB]=1-tanA·tanB
∴tan(A+B)=1
又0<A+B<π ∴A+B=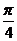
(再證必要性)
由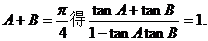
整理得(1+tanA)(1+tanB)=2
說明:可類似地證明以下命題:
(1)若α+β=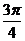 ,則(1-tanα)(1-tanβ)=2;
,則(1-tanα)(1-tanβ)=2;
(2)若α+β= ,則(1+tanα)(1+tanβ)=2;
,則(1+tanα)(1+tanβ)=2;
(3)若α+β= ,則(1-tanα)(1-tanβ)=2
,則(1-tanα)(1-tanβ)=2
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com