
7、.解:(1)設等比數列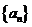 的公比為
的公比為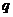 .
.
則由等比數列的通項公式 得
得 ,
,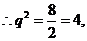
又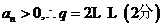
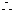 數列
數列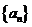 的通項公式是
的通項公式是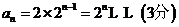 .
.
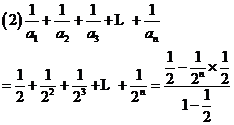
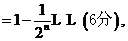
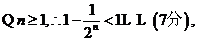
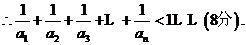
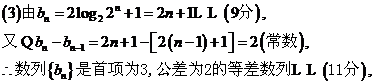
 數列
數列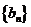 的前100項和是
的前100項和是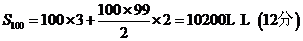
6、解:(Ⅰ)由 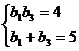 知
知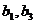 是方程
是方程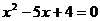 的兩根,注意到
的兩根,注意到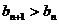 得
得 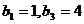 .……2分
.……2分
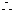
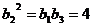 得
得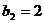 .
.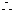
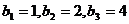
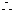 等比數列.
等比數列. 的公比為
的公比為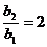 ,
,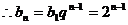 ……4分
……4分
(Ⅱ)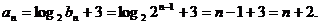 ……5分
……5分
∵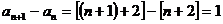 ……7分
……7分
 數列
數列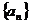 是首相為3,公差為1的等差數列. ……8分
是首相為3,公差為1的等差數列. ……8分
(Ⅲ) 由(Ⅱ)知數列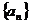 是首相為3,公差為1的等差數列,有
是首相為3,公差為1的等差數列,有
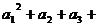 ……
……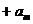 =
=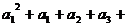 ……
……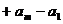
=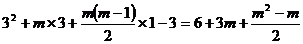 ……10分
……10分 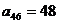
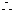
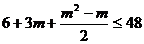 ,整理得
,整理得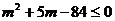 ,解得
,解得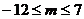 .
. ……11分
……11分
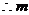 的最大值是7. ……12分
的最大值是7. ……12分
5、解:(I)證明: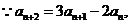
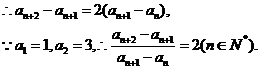
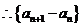 是以
是以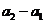
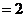 為首項,2為公比的等比數列。
為首項,2為公比的等比數列。
(II)解:由(I)得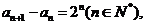
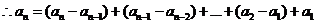
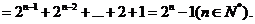
(III)證明: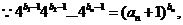
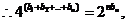
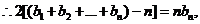 ①
①
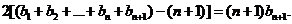 ②
②
②-①,得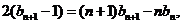 ……10分
……10分
即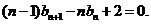 ③
③
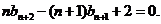 ④
④
④-③,得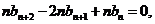
即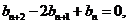
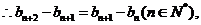
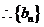 是等差數列.
是等差數列.
21. (Ⅰ)∵函數 f (x) 的圖象關于關于直線x=-對稱,
∴a≠0,-=-, ∴ b=3a①
∵其圖象過點(1,0),則a+b-=0 ②
由①②得a= , b= . 4分
(Ⅱ)由(Ⅰ)得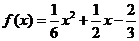 ,∴
,∴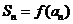 =
=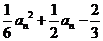
當n≥2時,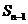 =
=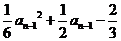 .
.
兩式相減得 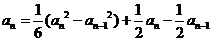
∴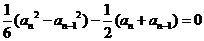 ,∴
,∴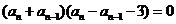

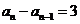 ,∴
,∴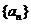 是公差為3的等差數列,且
是公差為3的等差數列,且
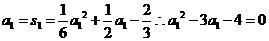
∴a1 = 4 (a1 =-1舍去)∴an =3n+1 9分
(Ⅲ)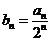 =
=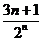 ,
,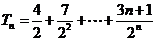 ①
①

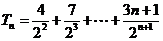 ②
②
①--② 得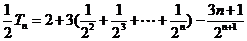
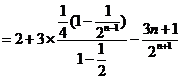
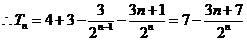
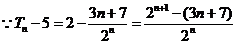 ,
,
(1) 當n=1、2時,Tn -5<0, ∴Tn <5;
(2) 當n=3時,Tn -5=0, ∴ Tn =5;
(3) 當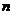 ≥ 4時,記 h (x)
= 2x+1-(3x+7), h ' (x)= 2x+1ln2-3,
≥ 4時,記 h (x)
= 2x+1-(3x+7), h ' (x)= 2x+1ln2-3,
當x >3時,有:h'(x)>23+1ln2-3=23×2×ln2-3=8ln22-3=8ln4-3>8-3>0,
則h(x)在(3, +¥)上單調遞增,∴ 當n≥4時,2n+1-(3n+7)>0 ∴Tn -5>0, ∴ Tn >5
綜上:當n≤2, Tn<5;當n=3, Tn=5;當n≥4, Tn>5. 14分
3、q 的最大值為 , 此時x=0,∴ 點P的坐標為(0,±). 14分
2、解:(1)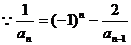 ,
,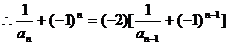 ,
,
又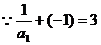 ,∴數列
,∴數列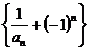 是首項為
是首項為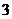 ,公比為
,公比為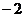 的等比數列.
的等比數列.
(2)依(Ⅰ)的結論有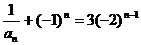 ,即
,即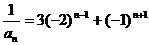 .
.
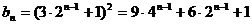 .
.
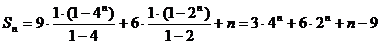 .
.
(3)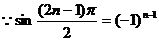 ,又由(Ⅱ)有
,又由(Ⅱ)有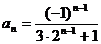
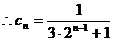 .
.
則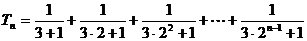
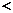 (
( 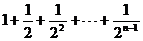 ) =
) = 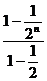
=( 1-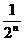 )<∴ 對任意的
)<∴ 對任意的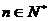 ,
,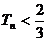 .
.
1、(1) 解法一:由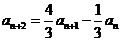 ,得
,得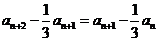 ,
,
∴數列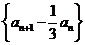 是常數列,
是常數列,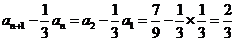 ,
,
即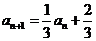 ,得
,得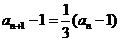 .
.
∴數列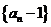 是首項為
是首項為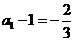 ,公比為
,公比為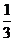 的等比數列,
的等比數列,
∴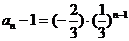 ,故數列
,故數列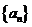 的通項公式為
的通項公式為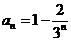 . …………5分
. …………5分
解法二:由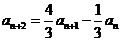 ,得
,得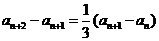 ,
,
∴數列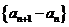 是首項為
是首項為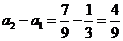 ,公比為
,公比為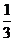 的等比數列,
的等比數列,
∴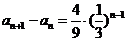 .
.
∴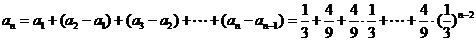
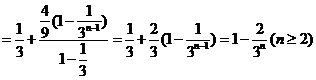 (*)
(*)
當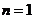 時,
時,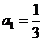 也適合(*),故數列
也適合(*),故數列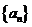 的通項公式為
的通項公式為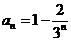 . ………5分
. ………5分
解法三:由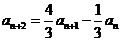 ,得
,得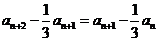 ,
,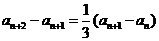 .
.
∴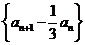 是常數列,
是常數列,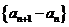 是首項為
是首項為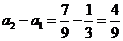 ,公比為
,公比為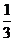 的等比數列.
的等比數列.
∴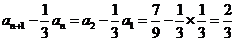 ,且
,且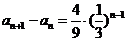 .
.
由上式聯立消去 ,解得:
,解得: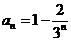 為數列
為數列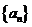 的通項公式. …………5分
的通項公式. …………5分
解法四:由已知,有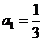 ,
,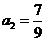 ,
,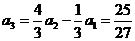 ,從而猜想:
,從而猜想: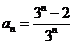 .
.
下用第二數學歸納法證明:
① 當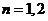 時,結論顯然成立.
時,結論顯然成立.
② 假設當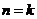 和
和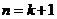 時結論成立,即
時結論成立,即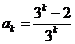 ,
,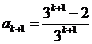 ,
,
則當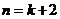 時,
時,
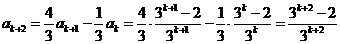 ,即當
,即當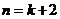 時結論也成立.
時結論也成立.
綜上,數列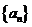 的通項公式為
的通項公式為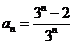 .
…………5分
.
…………5分
(2) 解: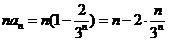 .
.
設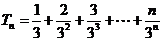 , ①
, ① 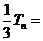
 . ②
. ②
①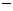 ②得:
②得: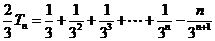
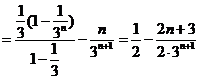 ,
,
∴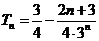 .
.
故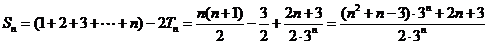 . …9分
. …9分
(3) 證: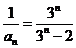 .
.
∵不等式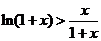 對
對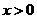 成立,令
成立,令 ,得
,得 ,即
,即
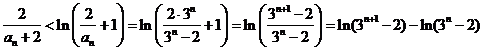 . 于是
. 于是
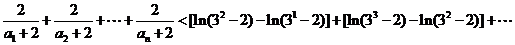
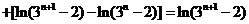 .
.
∴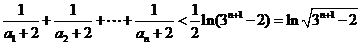 .
…………14分
.
…………14分
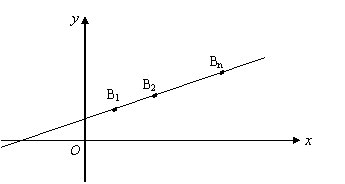
11、(2009番禺)已知點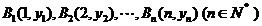 在直線
在直線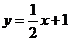 上,點
上,點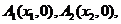
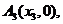 ……,
……,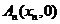 順次為
順次為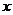 軸上的點,其中
軸上的點,其中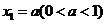 ,對于任意
,對于任意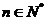 ,點
,點 構成以
構成以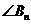 為頂角的等腰三角形, 設
為頂角的等腰三角形, 設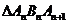 的面積為
的面積為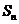 .
.
(1)
證明:數列 是等差數列;
是等差數列;
(2)
求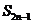 ;(用
;(用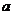 和
和 的代數式表示)
的代數式表示)
(3)
 設數列
設數列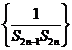 前
前 項和為
項和為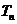 ,判斷
,判斷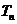 與
與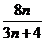 (
(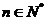 )的大小,并證明你的結論;
)的大小,并證明你的結論;
祥細答案:
10、(2009廣東六校一)已知數列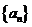 的首項
的首項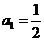 ,前
,前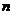 項和
項和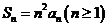 .
.
(Ⅰ)求數列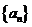 的通項公式;
的通項公式;
(Ⅱ)設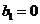 ,
,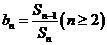 ,
,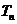 為數列
為數列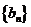 的前
的前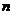 項和,求證:
項和,求證: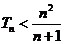 .
.
9、(2009潮南)在數列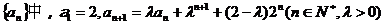
(1) 求數列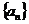 的通項公式;
的通項公式;
(2) 求數列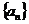 的前n項和
的前n項和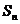 ;
;
(3) 證明存在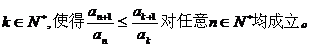
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com