
19.已知菱形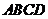 頂點
頂點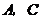 在橢圓
在橢圓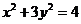 上,對角線
上,對角線 的斜率為1.
的斜率為1.
(Ⅰ)當直線 過點
過點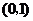 時,求直線
時,求直線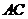 的方程;
的方程;
(Ⅱ)當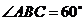 時,求菱形
時,求菱形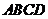 面積的最大值.
面積的最大值.
解:(Ⅰ)由題意 的方程為
的方程為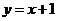 .因四邊形
.因四邊形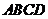 為菱形,所以
為菱形,所以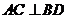 .
.
于是可設直線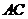 的方程為
的方程為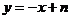 .由
.由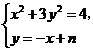 得
得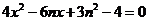 .
.
因為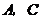 在橢圓上,所以
在橢圓上,所以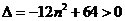 ,解得
,解得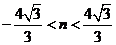 .
.
設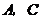 兩點坐標分別為
兩點坐標分別為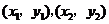 ,則
,則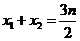 ,
,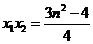 ,
,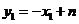 ,
,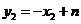 .所以
.所以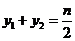 .所以
.所以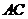 的中點坐標為
的中點坐標為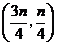 .
.
由四邊形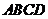 為菱形可知,點
為菱形可知,點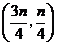 在直線
在直線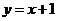 上,
上,
所以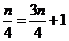 ,解得
,解得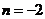 .所以直線
.所以直線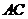 的方程為
的方程為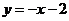 ,即
,即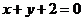 .
.
(Ⅱ)因為四邊形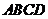 為菱形,且
為菱形,且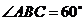 ,
,
所以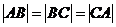 .所以菱形
.所以菱形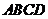 的面積
的面積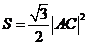 .由(Ⅰ)
.由(Ⅰ)
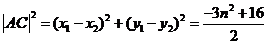 ,
,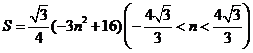 .
.
所以當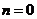 時,菱形
時,菱形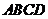 的面積取得最大值
的面積取得最大值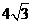 .
.
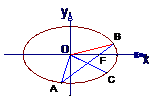
18.如圖 ,橢圓的中心在原點, 焦點在x軸上, 過其右焦點F作斜率為1的直線, 交橢圓于A、B兩點, 若橢圓上存在一點C, 使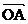 +
+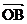 =
=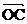 .
.
(1) 求橢圓的離心率;(2) 若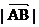 =15, 求著個橢圓的方程.
=15, 求著個橢圓的方程.
 解: (1)設橢圓的方程為
解: (1)設橢圓的方程為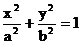 , 焦距為
, 焦距為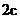 , 則直線l的方程為:
, 則直線l的方程為: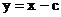 ,
,
代入橢圓方程, 得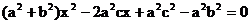 ,
,
設點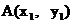 、
、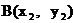 ,
,
則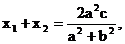
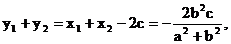
∵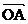 +
+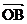
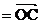 , ∴C點坐標為
, ∴C點坐標為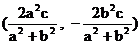 .
.
∵C點在橢圓上, ∴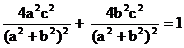 .∴
.∴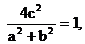
∴ 又
又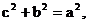 ∴
∴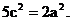 ∴
∴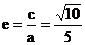
(2) ∵
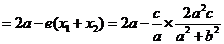
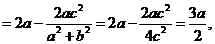 由已知
由已知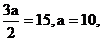 從而
從而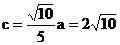 .
.
∴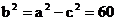 .故橢圓的方程為:
.故橢圓的方程為: 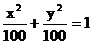 .
.
17.已知拋物線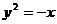 與直線
與直線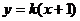 相交于A、B 兩點 ,
相交于A、B 兩點 ,
①求證;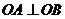 ;
;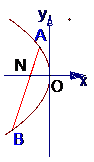 ②當
②當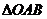 的面積等于
的面積等于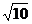 時,求
時,求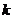 的值
的值
證明: ①設
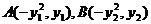 ;
; 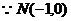
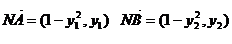 ,由A,N,B共線
,由A,N,B共線
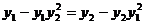
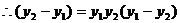 ,
,
又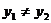
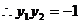
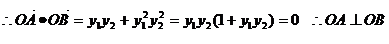
解② 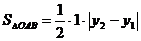 由
由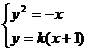 得
得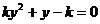
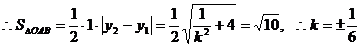
16.已知橢圓的焦點是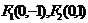 ,直線
,直線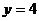 是橢圓的一條準線.
是橢圓的一條準線.
① 求橢圓的方程;② 設點P在橢圓上,且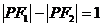 ,求
,求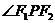 的余弦值.
的余弦值.
解:①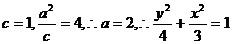 .
.
②設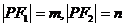 則
則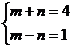

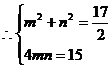
又 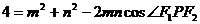
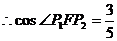 ,
, 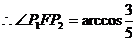

15.一個酒杯的軸截面是拋物線的一部分,它的方程是x2=2y(0≤y≤20) 在杯內放入一個玻璃球,要使球觸及酒杯底部,求玻璃球的半徑r的范圍
在杯內放入一個玻璃球,要使球觸及酒杯底部,求玻璃球的半徑r的范圍
解:玻璃球的軸截面的方程為x2+(y-r)2=r2由x2=2y,x2+(y-r)2=r2,
得y2+2(1-r)y=0,由Δ=4(1-r)2=0,得r=1 答案:0<r≤1
14.設橢圓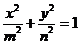 (
(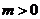 ,
,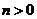 )的右焦點與拋物線
)的右焦點與拋物線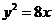 的焦點相同,離心率為
的焦點相同,離心率為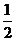 ,則此橢圓的方程為__________
,則此橢圓的方程為__________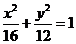
13.已知拋物線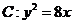 的焦點為
的焦點為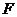 ,準線與
,準線與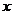 軸的交點為
軸的交點為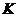 ,點
,點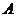 在
在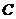 上且
上且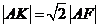 ,則
,則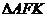 的面積為_________
的面積為_________
12.已知點P是拋物線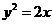 上的一個動點,則點P到點(0,2)的距離與P到該拋物線準線的距離之和的最小值為_________
上的一個動點,則點P到點(0,2)的距離與P到該拋物線準線的距離之和的最小值為_________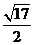
11.設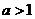 ,則雙曲線
,則雙曲線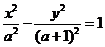 的離心率
的離心率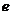 的取值范圍是_______
的取值范圍是_______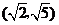
10.已知點P在拋物線y2 = 4x上,那么點P到點Q(2,-1)的距離與點P到拋物線焦點距離之和取得最小值時,點P的坐標為____________(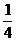 ,-1)
,-1)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com