日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

5.答案：D

解析：首先討論分母1－x(1－x)的取值范圍：1－x(1－x)=x²－x+1=(x－)²+≥.因此，有0<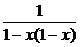≤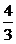.所以，f(x)的最大值為.

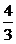評述：該題側重考查考生“化生為熟”的識別能力及對代數式的轉化能力.

4.答案：C

解析：首先作出函數y=|x|與g(x)=x(2－x)=－x²+2x=－(x－1)²+1的圖象(如圖2-13).利用圖象分別確定其單調區間.y=|x|的增區間為［0，+∞，y=x(2－x)單調增區間為(－∞，1.

(1)　　　　　　　　　　　　　 (2)

圖2-13

評述：該題側重考查考生“化生為熟”的識別能力以及對問題的轉化能力.

3.答案：C

解析：y=2^－x的值域為y>0，y=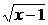的值域為y≥0.因此，其交集為y>0.

評述：本題是文科的“姊妹題”，體現了數學對文、理科學生的認識及要求的區別，這是高考命題的方向.

2.答案：C

解析：y=2^x的值域為y>0，y=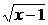的值域為y≥0.因此，其交集為y>0.

評述：本題考查了考生對集合代表元素的認識，利用函數的圖象確定函數的值域.體現了數形結合的數學思想.

1.答案：D

解析：f(4x)=，依題意，有=x.解得：x=.

評述：本題主要考查函數的對應法則、函數與方程的關系及求方程的根.

116.(1994全國，文22)已知函數f(x)=log_ax(a>0且a≠1，x∈(0，+∞)).若x₁，x₂∈(0，+∞)，判斷［f(x₁)+f(x₂)］與f()的大小，并加以證明.

注：加“*”的試題為應用題，其他章與此同.

●答案解析

115.(1995全國文，21)解方程3^x+2－3^2－x=80.

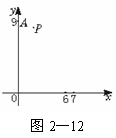
114.(1996上海，20)在如圖2-12所示的直角坐標系中，一運動物體經過點A(0，9)，其軌跡方程為y=ax²+c(a＜0)，D=(6，7)為x軸上的給定區間.

(1)為使物體落在D內，求a的取值范圍；

(2)若物體運動時又經過點P(2，8.1)，問它能否落在D內?并說明理由.

113.(1999全國文，19)解方程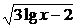－3lgx+4=0.

112.(2000上海，19)已知函數f(x)＝，x∈［1，+∞．

(1)當a＝時，求函數f(x)的最小值；

(2)若對任意x∈［1，+∞，f(x)＞0恒成立，試求實數a的取值范圍.