
(一)函數的性質
函數的性質是研究初等函數的基石,也是高考考查的重點內容.在復習中要肯于在對定義的深入理解上下功夫.
復習函數的性質,可以從“數”和“形”兩個方面,從理解函數的單調性和奇偶性的定義入手,在判斷和證明函數的性質的問題中得以鞏固,在求復合函數的單調區間、函數的最值及應用問題的過程中得以深化.具體要求是:
1.正確理解函數單調性和奇偶性的定義,能準確判斷函數的奇偶性,以及函數在某一區間的單調性,能熟練運用定義證明函數的單調性和奇偶性.
2.從數形結合的角度認識函數的單調性和奇偶性,深化對函數性質幾何特征的理解和運用,歸納總結求函數最大值和最小值的常用方法.
3.培養學生用運動變化的觀點分析問題,提高學生用換元、轉化、數形結合等數學思想方法解決問題的能力.
這部分內容的重點是對函數單調性和奇偶性定義的深入理解.
函數的單調性只能在函數的定義域內來討論.函數y=f(x)在給定區間上的單調性,反映了函數在區間上函數值的變化趨勢,是函數在區間上的整體性質,但不一定是函數在定義域上的整體性質.函數的單調性是對某個區間而言的,所以要受到區間的限制.
對函數奇偶性定義的理解,不能只停留在f(-x)=f(x)和f(-x)=-f(x)這兩個等式上,要明確對定義域內任意一個x,都有f(-x)=f(x),f(-x)=-f(x)的實質是:函數的定義域關于原點對稱.這是函數具備奇偶性的必要條件.稍加推廣,可得函數f(x)的圖象關于直線x=a對稱的充要條件是對定義域內的任意x,都有f(x+a)=f(a-x)成立.函數的奇偶性是其相應圖象的特殊的對稱性的反映.
這部分的難點是函數的單調性和奇偶性的綜合運用.根據已知條件,調動相關知識,選擇恰當的方法解決問題,是對學生能力的較高要求.
1.對函數單調性和奇偶性定義的理解
例4.下面四個結論:①偶函數的圖象一定與y軸相交;②奇函數的圖象一定通過原點;③偶函數的圖象關于y軸對稱;④既是奇函數又是偶函數的函數一定是f(x)=0(x∈R),其中正確命題的個數是 ( )
A.1 B.2
C.3 D.4
分析:偶函數的圖象關于y軸對稱,但不一定相交,因此③正確,①錯誤.
奇函數的圖象關于原點對稱,但不一定經過原點,因此②不正確.
若y=f(x)既是奇函數,又是偶函數,由定義可得f(x)=0,但不一定x∈R,如例1中的(3),故④錯誤,選A.
說明:既奇又偶函數的充要條件是定義域關于原點對稱且函數值恒為零.
2.復合函數的性質
復合函數y=f[g(x)]是由函數u=g(x)和y=f(u)構成的,因變量y通過中間變量u與自變量x建立起函數關系,函數u=g(x)的值域是y=f(u)定義域的子集.
復合函數的性質由構成它的函數性質所決定,具備如下規律:
(1)單調性規律
如果函數u=g(x)在區間[m,n]上是單調函數,且函數y=f(u)在區間[g(m),g(n)] (或[g(n),g(m)])上也是單調函數,那么
若u=g(x),y=f(u)增減性相同,則復合函數y=f[g(x)]為增函數;若u=g(x),y= f(u)增減性不同,則y=f[g(x)]為減函數.
(2)奇偶性規律
若函數g(x),f(x),f[g(x)]的定義域都是關于原點對稱的,則u=g(x),y=f(u)都是奇函數時,y=f[g(x)]是奇函數;u=g(x),y=f(u)都是偶函數,或者一奇一偶時,y= f[g(x)]是偶函數.
例5.若y=log (2-ax)在[0,1]上是x的減函數,則a的取值范圍是( )
(2-ax)在[0,1]上是x的減函數,則a的取值范圍是( )
A.(0,1) B.(1,2)
C.(0,2) D.[2,+∞)
分析:本題存在多種解法,但不管哪種方法,都必須保證:①使log (2-ax)有意義,即a>0且a≠1,2-ax>0.②使log
(2-ax)有意義,即a>0且a≠1,2-ax>0.②使log (2-ax)在[0,1]上是x的減函數.由于所給函數可分解為y=log
(2-ax)在[0,1]上是x的減函數.由于所給函數可分解為y=log u,u=2-ax,其中u=2-ax在a>0時為減函數,所以必須a>1;③[0,1]必須是y=log
u,u=2-ax,其中u=2-ax在a>0時為減函數,所以必須a>1;③[0,1]必須是y=log (2-ax)定義域的子集.
(2-ax)定義域的子集.
解法一:因為f(x)在[0,1]上是x的減函數,所以f(0)>f(1),
即log 2>log
2>log (2-a).
(2-a).
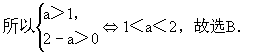

解法二:由對數概念顯然有a>0且a≠1,因此u=2-ax在[0,1]上是減函數,y= log u應為增函數,得a>1,排除A,C,再令
u應為增函數,得a>1,排除A,C,再令
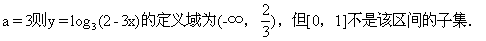

故排除D,選B.
說明:本題為1995年全國高考試題,綜合了多個知識點,無論是用直接法,還是用排除法都需要概念清楚,推理正確.
3.函數單調性與奇偶性的綜合運用
例6.甲、乙兩地相距Skm,汽車從甲地勻速行駛到乙地,速度不得超過c km/h,已知汽車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度v(km/h)的平方成正比,比例系數為b;固定部分為a元.
(1)把全程運輸成本y(元)表示為速度v(km/h)的函數,并指出這個函數的定義域;
(2)為了使全程運輸成本最小,汽車應以多大速度行駛.
分析:(1)難度不大,抓住關系式:全程運輸成本=單位時間運輸成本×全程運輸時間,而全程運輸時間=(全程距離)÷(平均速度)就可以解決.


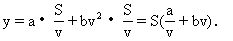

故所求函數及其定義域為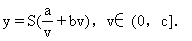



但由于題設條件限制汽車行駛速度不超過ckm/h,所以(2)的解決需要
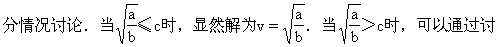

論函數的增減性來解決.

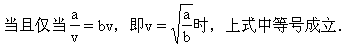
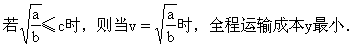
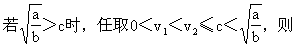
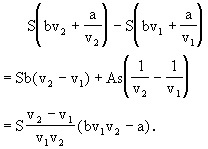
由于v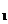 v
v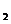 >0,v
>0,v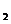 -v
-v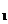 >0,并且
>0,并且
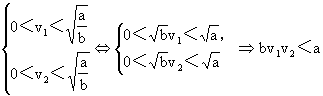
又S>0,所以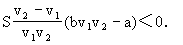 即
即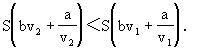
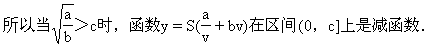
則當v=c時,y取最小值.

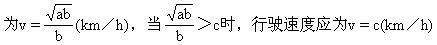
說明:此題是1997年全國高考試題.由于限制汽車行駛速度不得超過c,因而求最值的方法也就不完全是常用的方法,再加上字母的抽象性,使難度有所增大.
3.求函數解析式舉例
例3.已知xy<0,并且4x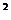 -9y
-9y =36.由此能否確定一個函數關系y=f(x)?如果能,求出其解析式、定義域和值域;如果不能,請說明理由.
=36.由此能否確定一個函數關系y=f(x)?如果能,求出其解析式、定義域和值域;如果不能,請說明理由.
分析: 4x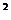 -9y
-9y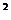 =36在解析幾何中表示雙曲線的方程,僅此當然不能確定一個函數關系y=f(x),但加上條件xy<0呢?
=36在解析幾何中表示雙曲線的方程,僅此當然不能確定一個函數關系y=f(x),但加上條件xy<0呢?
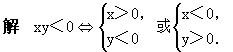

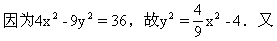

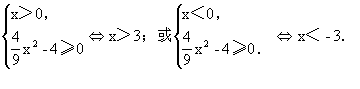

所以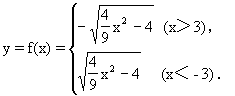

因此能確定一個函數關系y=f(x).其定義域為(-∞,-3)∪(3,+∞).且不難得到其值域為(-∞,0)∪(0,+∞).
說明:本例從某種程度上揭示了函數與解析幾何中方程的內在聯系.任何一個函數的解析式都可看作一個方程,在一定條件下,方程也可轉化為表示函數的解析式.求函數解析式還有兩類問題:
(1)求常見函數的解析式.由于常見函數(一次函數,二次函數,冪函數,指數函數,對數函數,三角函數及反三角函數)的解析式的結構形式是確定的,故可用待定系數法確定其解析式.這里不再舉例.
(2)從生產、生活中產生的函數關系的確定.這要把有關學科知識,生活經驗與函數概念結合起來,舉例也宜放在函數復習的以后部分.
2.求函數值域的基本類型和常用方法
函數的值域是由其對應法則和定義域共同決定的.其類型依解析式的特點分可分三類:(1)求常見函數值域;(2)求由常見函數復合而成的函數的值域;(3)求由常見函數作某些“運算”而得函數的值域. 
2.
由給定函數解析式求其定義域這類問題的代表,實際上是求使給定式有意義的x的取值范圍.它依賴于對各種式的認識與解不等式技能的熟練.這里的最高層次要求是給出的解析式還含有其他字
例2.已知函數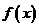 定義域為(0,2),求下列函數的定義域:
定義域為(0,2),求下列函數的定義域:
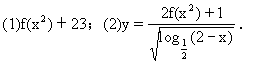

分析:x的函數f(x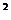 )是由u=x
)是由u=x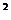 與f(u)這兩個函數復合而成的復合函數,其中x是自變量,u是中間變量.由于f(x),f(u)是同一個函數,故(1)為已知0<u<2,即0<x
與f(u)這兩個函數復合而成的復合函數,其中x是自變量,u是中間變量.由于f(x),f(u)是同一個函數,故(1)為已知0<u<2,即0<x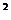 <2.求x的取值范圍.
<2.求x的取值范圍.
解:(1)由0<x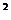 <2, 得
<2, 得
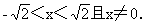

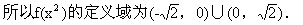

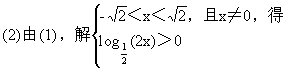
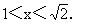

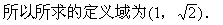

說明:本例(1)是求函數定義域的第二種類型,即不給出f(x)的解析式,由f(x)的定義域求函數f[g(x)]的定義域.關鍵在于理解復合函數的意義,用好換元法.(2)是二種類型的綜合.
求函數定義域的第三種類型是一些數學問題或實際問題中產生的函數關系,求其定義域。
1.
求函數定義域的基本類型和常用方法
3.通過對分段定義函數,復合函數,抽象函數等的認識,進一步體會函數關系的本質,進一步樹立運動變化,相互聯系、制約的函數思想,為函數思想的廣泛運用打好基礎.
本部分的難點首先在于克服“函數就是解析式”的片面認識,真正明確不僅函數的對應法則,而且其定義域都包含著對函數關系的制約作用,并真正以此作為處理問題的指導.其次在于確定函數三要素、求反函數等課題的綜合性,不僅要用到解方程,解不等式等知識,還要用到換元思想、方程思想等與函數有關概念的結合.
Ⅰ 深化對函數概念的認識
例1.下列函數中,不存在反函數的是 ( )
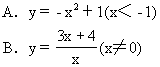
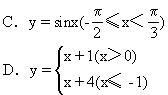

分析:處理本題有多種思路.分別求所給各函數的反函數,看是否存在是不好的,因為過程太繁瑣.
從概念看,這里應判斷對于給出函數值域內的任意值,依據相應的對應法則,是否在其定義域內都只有惟一確定的值與之對應,因此可作出給定函數的圖象,用數形結合法作判斷,這是常用方法。
此題作為選擇題還可采用估算的方法.對于D,y=3是其值域內一個值,但若y=3,則可能x=2(2>1),也可能x=-1(-1≤-1).依據概念,則易得出D中函數不存在反函數.于是決定本題選D.
說明:不論采取什么思路,理解和運用函數與其反函數的關系是這里解決問題的關鍵.
由于函數三要素在函數概念中的重要地位,那么掌握確定函數三要素的基本方法當然成了函數概念復習中的重要課題.
例1.(重慶市)函數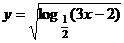 的定義域是( D )
的定義域是( D )
A、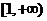 B、
B、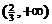 C、
C、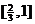 D、
D、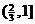

例2.(天津市)函數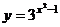 (
(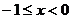 )的反函數是( D )
)的反函數是( D )
A、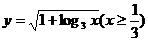 B、
B、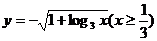

C、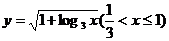 D、
D、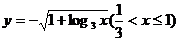

也有個別小題的難度較大,如
例3.(北京市)函數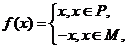 其中P、M為實數集R的兩個非空子集,又規定
其中P、M為實數集R的兩個非空子集,又規定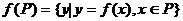 ,
,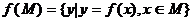 ,給出下列四個判斷:
,給出下列四個判斷:
①若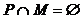 ,則
,則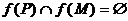 ②若
②若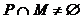 ,則
,則

③若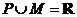 ,則
,則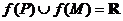 ④若
④若 ,則
,則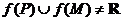

其中正確判斷有( B )
A、 1個 B、 2個 C、 3個 D、 4個
分析:若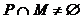 ,則只有
,則只有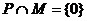 這一種可能.②和④是正確的.
這一種可能.②和④是正確的.

Ⅱ 系統小結確定函數三要素的基本類型與常用方法
2.系統歸納求函數定義域、值域、解析式、反函數的基本方法.在熟練有關技能的同時,注意對換元、待定系數法等數學思想方法的運用.
函數有二種定義,一是變量觀點下的定義,一是映射觀點下的定義.復習中不能僅滿足對這兩種定義的背誦,而應在判斷是否構成函數關系,兩個函數關系是否相同等問題中得到深化,更應在有關反函數問題中正確運用.具體要求是:
1.深化對函數概念的理解,明確函數三要素的作用,并能以此為指導正確理解函數與其反函數的關系

也許黛玉最顯著的標志就是那雙哭腫的像桃核一樣的眼睛了,不知道這玉兒的眼淚為什么如此的多,哭得讓人斷腸。
在大觀園中,這位恐怕就是最引人注目的了吧。由于家庭變故,從小寄居外祖母家的她變得小心翼翼,生怕被人恥笑了去,正是這樣,才使得她多疑、猜忌。然而在骨子里,黛玉有的是水一樣的柔情。
對待自己的愛情。黛玉敢于追求,她愿意表露出來,希望寶玉能了解.在這一點上,她突破了封建禮教對女子的束縛,打破了這些規矩。盡管她最后含恨而死,但仍然讓我們看到了一個敢愛敢恨,敢突破,敢創新的奇女子。

雖然黛玉有時會有一些小性子,小心眼,但這始終無法抹去遮住和她獨有的光輝。黛玉啊,你就像是一顆星,雖鋒芒畢露,難免刺痛他人,可你是那么特別,與眾不同。
你讓我看到了一個女人特有的氣質。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com