
1.[答案]i
[解析]設z=a+bi,則(a+bi )(1+i)
=1-i,即a-b+(a+b)i=1-i,由 ,解得a=0,b=-1,所以z=-i,
,解得a=0,b=-1,所以z=-i, =i
=i
1. 若復數 z 滿足z (1+i) =1-i (I是虛數單位),則其共軛復數 =__________________ .
=__________________ .
23.[解](1)由 得
得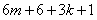 ,
,
整理后,可得
 、
、 ,
, 為整數
為整數
 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)當 時,則
時,則
 即
即 ,其中
,其中 是大于等于
是大于等于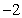 的整數
的整數
反之當 時,其中
時,其中 是大于等于
是大于等于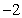 的整數,則
的整數,則 ,
,
顯然 ,其中
,其中

 、
、 滿足的充要條件是
滿足的充要條件是 ,其中
,其中 是大于等于
是大于等于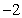 的整數
的整數
(3)設
當 為偶數時,
為偶數時,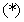 式左邊為偶數,右邊為奇數,
式左邊為偶數,右邊為奇數, 

當 為偶數時,
為偶數時,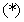 式不成立。
式不成立。
由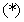 式得
式得 ,整理得
,整理得
當 時,符合題意。
時,符合題意。
當 ,
, 為奇數時,
為奇數時,


 由
由 ,得
,得

 當
當 為奇數時,此時,一定有
為奇數時,此時,一定有 和
和 使上式一定成立。
使上式一定成立。
 當
當 為奇數時,命題都成立。
為奇數時,命題都成立。 

23.(本題滿分18分)本題共有3個小題,第1小題滿分5分,第2小題滿分5分,第3小題滿分8分.
已知 是公差為d的等差數列,
是公差為d的等差數列, 是公比為q的等比數列
是公比為q的等比數列
(1)若  ,是否存在
,是否存在 ,有
,有 ?請說明理由;
?請說明理由;
(2)若 (a、q為常數,且aq
(a、q為常數,且aq 0)對任意m存在k,有
0)對任意m存在k,有 ,試求a、q滿足的充要條件;
,試求a、q滿足的充要條件;
(3)若 試確定所有的p,使數列
試確定所有的p,使數列 中存在某個連續p項的和式數列中
中存在某個連續p項的和式數列中 的一項,請證明.
的一項,請證明. 

22.[解](1)設雙曲線 的方程為
的方程為
 ,解額
,解額 雙曲線
雙曲線 的方程為
的方程為
(2)直線 ,直線
,直線
由題意,得 ,解得
,解得
(3)[證法一]設過原點且平行于 的直線
的直線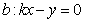
則直線 與
與 的距離
的距離 當
當 時,
時,
又雙曲線 的漸近線為
的漸近線為



 雙曲線
雙曲線 的右支在直線
的右支在直線 的右下方,
的右下方,
 雙曲線
雙曲線 右支上的任意點到直線
右支上的任意點到直線 的距離大于
的距離大于 。
。
故在雙曲線 的右支上不存在點
的右支上不存在點 ,使之到直線
,使之到直線 的距離為
的距離為
[證法二]假設雙曲線 右支上存在點
右支上存在點 到直線
到直線 的距離為
的距離為 ,
,
則
由(1)得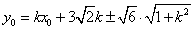
設 ,
,
當 時,
時, ;
;

將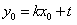 代入(2)得
代入(2)得
 ,
, 


 方程
方程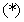 不存在正根,即假設不成立,
不存在正根,即假設不成立,
故在雙曲線 的右支上不存在點
的右支上不存在點 ,使之到直線
,使之到直線 的距離為
的距離為
22.(本題滿分16分)本題共有3個小題,第1小題滿分4分,第2小題滿分4分,第3小題滿分8分.
已知雙曲線C的中心是原點,右焦點為F ,一條漸近線m:
,一條漸近線m: ,設過點A
,設過點A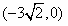 的直線l的方向向量
的直線l的方向向量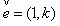 。
。
(1) 求雙曲線C的方程;
(2) 若過原點的直線 ,且a與l的距離為
,且a與l的距離為 ,求K的值;
,求K的值;
(3) 證明:當 時,在雙曲線C的右支上不存在點Q,使之到直線l的距離為
時,在雙曲線C的右支上不存在點Q,使之到直線l的距離為 .
.
21.(本題滿分16分)本題共有2個小題,第1小題滿分6分,第2小題滿分10分 .有時可用函數

描述學習某學科知識的掌握程度.其中 表示某學科知識的學習次數(
表示某學科知識的學習次數( ),
),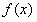 表示對該學科知識的掌握程度,正實數a與學科知識有關.
表示對該學科知識的掌握程度,正實數a與學科知識有關.
(1)證明:當x  7時,掌握程度的增長量f(x+1)- f(x)總是下降;
7時,掌握程度的增長量f(x+1)- f(x)總是下降;
(2)根據經驗,學科甲、乙、丙對應的a的取值區間分別為(115,121],(121,127],
(127,133].當學習某學科知識6次時,掌握程度是85%,請確定相應的學科.
21題。證明(1)當 時,
時,
而當 時,函數
時,函數 單調遞增,且
單調遞增,且
故函數 單調遞減
單調遞減 

當 時,掌握程度的增長量
時,掌握程度的增長量 總是下降
總是下降
(2)有題意可知
整理得
解得 …….13分
…….13分
由此可知,該學科是乙學科……………..14分
20.(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2小題滿分8分 .
已知ΔABC的角A、B、C所對的邊分別是a、b、c,設向量 ,
,
 ,
,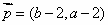 .
.
(1) 若 //
// ,求證:ΔABC為等腰三角形;
,求證:ΔABC為等腰三角形;
(2) 若 ⊥
⊥ ,邊長c = 2,角C =
,邊長c = 2,角C =  ,求ΔABC的面積 .
,求ΔABC的面積 .
20題。證明:(1)
即 ,其中R是三角形ABC外接圓半徑,
,其中R是三角形ABC外接圓半徑,
 為等腰三角形
為等腰三角形
解(2)由題意可知

由余弦定理可知,
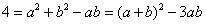





19.解:原方程的根為 




19.(本題滿分14分)
已知復數 (a、b
(a、b )(I是虛數單位)是方程
)(I是虛數單位)是方程 的根 . 復數
的根 . 復數 (
( )滿足
)滿足 ,求 u 的取值范圍 .
,求 u 的取值范圍 .
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com