
題目列表(包括答案和解析)
| |||||||||||
| x2 |
| 4 |
| 2 |
| OA |
| OB |
⊙O1和⊙O2的極坐標方程分別為 ,
, .
.
⑴把⊙O1和⊙O2的極坐標方程化為直角坐標方程;
⑵求經過⊙O1,⊙O2交點的直線的直角坐標方程.
【解析】本試題主要是考查了極坐標的返程和直角坐標方程的轉化和簡單的圓冤啊位置關系的運用
(1)中,借助于公式 ,
, ,將極坐標方程化為普通方程即可。
,將極坐標方程化為普通方程即可。
(2)中,根據上一問中的圓的方程,然后作差得到交線所在的直線的普通方程。
解:以極點為原點,極軸為x軸正半軸,建立平面直角坐標系,兩坐標系中取相同的長度單位.
(I) ,
, ,由
,由 得
得 .所以
.所以 .
.
即 為⊙O1的直角坐標方程.
為⊙O1的直角坐標方程.
同理 為⊙O2的直角坐標方程.
為⊙O2的直角坐標方程.
(II)解法一:由 解得
解得 ,
,
即⊙O1,⊙O2交于點(0,0)和(2,-2).過交點的直線的直角坐標方程為y=-x.
解法二: 由 ,兩式相減得-4x-4y=0,即過交點的直線的直角坐標方程為y=-x
,兩式相減得-4x-4y=0,即過交點的直線的直角坐標方程為y=-x
這個算法又叫“韓信點兵”.相傳韓信才略過人,領兵打仗時,為了對敵方保密,從不點自己軍隊的人數,只是讓他的士兵以三人一排很快地從他面前過去,再以五人一排走一次,最后以七人一排走過去,由于隊伍走得很快,別人根本來不及數有多少人.然而韓信只對各隊士兵的最后一排掠一眼,就知道總數了,他利用的就是上面的這個口訣.
畫出程序框圖,并編寫程序解決“韓信點兵”問題.
古希臘數學家丟番圖(公元250年前后)在《算術》中就提到了一元二次![]() 方程的問題,不過當時古希臘人還沒有尋求到它的求根公式,只能用圖解等方法來求解。在歐幾里得的《幾何原本》中,形如
方程的問題,不過當時古希臘人還沒有尋求到它的求根公式,只能用圖解等方法來求解。在歐幾里得的《幾何原本》中,形如![]() (a>0,b>0)的方程的圖解法是:如圖,以
(a>0,b>0)的方程的圖解法是:如圖,以![]() 和b為兩直角邊做Rt△ABC,再在斜邊上截取
和b為兩直角邊做Rt△ABC,再在斜邊上截取![]() ,則AD的長就是所求方程的解。
,則AD的長就是所求方程的解。
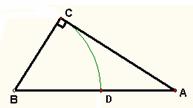
(1)請用含字母a、b的代數式表示AD的長。
(2)請利用你已學的知識說明該圖解法的正確性,并說說這種解法的遺憾之處。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com